
In molte applicazioni è spesso necessario generare numeri casuali distribuiti più o meno uniformemente in un determinato intervallo, ma l’ordine dei programmi e dei circuiti logici rende difficoltosa questa operazione. Ecco allora alcune utili tecniche.
A parte la realizzazione di un giogo di dadi, la generazione di numeri casuali viene utilizzata in molteplici applicazioni e spesso in modo completamente trasparente all’utilizzatore. A esempio in una comunicazione dati su Ethernet i dati vengono trasmessi allo scadere di un breve intervallo di tempo di durata casuale (o pseudo tale) in modo da ridurre al minimo la probabilità di collisione dei pacchetti dati. Un’altra applicazione in cui la generazione dei numeri casuali è fondamentale è la crittografia dati in cui un numero random viene utilizzato come chiave di codifica e decodifica dei dati. Anche se la generazione di un numero casuale può apparire una cosa semplice, in realtà la cosa è piuttosto complicata dal momento che anche il naturale disordine delle cose potrebbe risultare troppo ordinato! Vediamo allora alcune tecniche che potrete utilizzare nei vostri progetti.
COSA SONO I NUMERI CASUALI?
Non esiste una definizione unica e generale di numero casuale, essa infatti dipende spesso dal contesto. Il concetto stesso di numero casuale non è assoluto, in quanto un numero o una sequenza di numeri possono essere casuali per un osservatore, ma non esserlo per un altro (che conosce la legge con cui essi vengono generati). Per semplicità di seguito indicheremo con “numero casuale” un numero, selezionato grazie ad un processo aleatorio, da un insieme finito di numeri. Con questa definizione abbiamo spostato il concetto di casualità dal numero (o dalla sequenza di numeri) al processo di selezione. Questo particolare risulterà utile in seguito. Va notato che nella precedente definizione avremmo potuto sostituire il termine “numero” con “simbolo” o con “cifra”. In molti casi infatti il problema della generazione di numeri casuali, viene ricondotto alla generazione casuale di una sequenza di 0 e di 1, da cui si possono ricavare numeri in qualsiasi formato (interi, con segno in complemento a due, fixed-point, floating-point, ecc...) o stringhe di lunghezza arbitraria. È possibile caratterizzare un processo aleatorio da diversi punti di vista. Una delle caratteristiche più importanti è la sua distribuzione di probabilità. Questa fornisce informazioni su qual è la probabilità che ciascun elemento dell’insieme venga selezionato. In molti casi si considerano e si utilizzano dei processi caratterizzati da una distribuzione uniforme. Questo significa che ogni elemento ha la stessa probabilità degli altri di essere selezionato (asintoticamente, cioè se si suppone di condurre un numero infinito di estrazioni). Se si rappresentano su un grafico gli elementi e la loro rispettiva probabilità di essere estratti, si ottiene un grafico “rettangolare” (figura 1a). Dal momento che la probabilità viene espressa come un numero reale compreso tra 0 ed 1, in cui 0 rappresenta l’evento impossibile, ed 1 quello certo, in una distribuzione uniforme ciascun elemento avrà una probabilità 1/N di essere selezionato, dove N è il numero di elementi (la somma di tutte le probabilità deve fare 1, dal momento che in un’estrazione almeno uno degli elementi viene scelto di sicuro). La distribuzione uniforme è tipica dei processi aleatori “artificiali” come lancio di dadi, lotterie, roulette, ed è anche la più utilizzata in pratica nella applicazioni. Un’altra distribuzione di probabilità molto comune è quella gaussiana o “normale”, dalla tipica forma a campana (figura 1b).
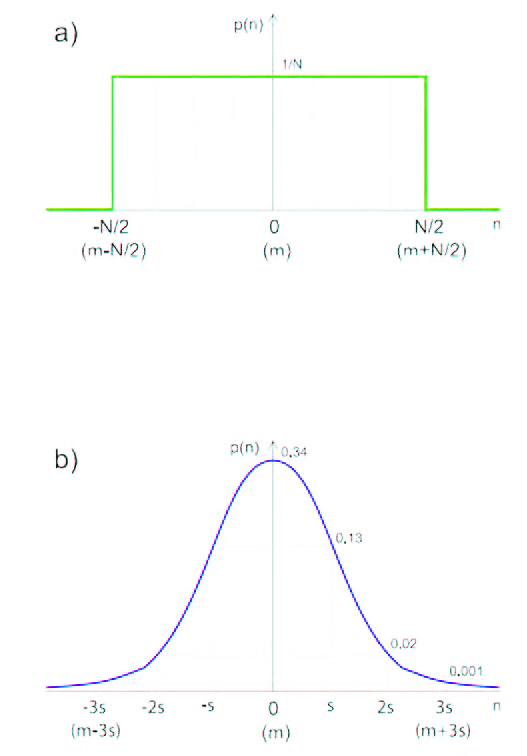
Figura 1: distribuzione di probabilità uniforme (a) e gaussiana (b).
In questo caso i valori più piccoli (o comunque più vicini al centro della curva) hanno maggiore probabilità di essere estratti rispetto a quelli più grandi (distanti dal centro). La distribuzione gaussiana è importante perché è tipica dei processi naturali (es. rumore di molti componenti elettronici, o di molti canali di telecomunicazione, errori nelle misure e conversioni A/D e D/A, ecc...), e viene quindi spesso utilizzata per simulare questi ultimi (per esempio nel campo delle telecomunicazioni o dell’elaborazione dei segnali). Un’altra importante caratteristica di una sequenza casuale è l’indipendenza statistica dei suoi termini, cioè la misura di quanto l’estrazione di un numero dipende da quello o quelli estratti precedentemente. Chiaramente in una sequenza random ideale gli elementi dovrebbero essere statisticamente indipendenti. Una misura dell’indipendenza statistica dei vari numeri generati è ottenibile ad esempio calcolando l’autocorrelazione o l’entropia (di vario ordine) della sequenza. Senza entrare nei dettagli matematici, è sufficiente sapere che l’entropia fornisce una misura di quanto è probabile (o prevedibile) trovare un numero nella sequenza, o di trovarlo dopo un altro o una certa stringa di numeri estratti. Più l’entropia è alta, più la sequenza è imprevedibile, e quindi “casuale” nel senso comune del termine (anche se contiene più “informazione” secondo Shannon). Purtroppo come vedremo in pratica ottenere sequenze non prevedibili e con una buona distribuzione è abbastanza difficile.
GENERARE NUMERI PSEUDO-CASUALI
Come è facile immaginare, non è possibile generare delle sequenze casuali vere utilizzando degli algoritmi deterministici (implementati via software o tramite circuiti logici), si possono al massimo generare delle sequenze “pseudo-casuali”, cioè sequenze apparentemente random, ma che in realtà sono perfettamente prevedibili, e che possono anche ripetersi dopo un certo numero di estrazioni. Di solito in questi casi si parte da un valore iniziale detto “seme”, che determina interamente la sequenza che verrà estratta di seguito. In molti casi il seme è scelto con un meccanismo casuale esterno, e quindi la sequenza risulta relativamente imprevedibile. Questo tipo di generatori ha due grossi vantaggi:
- la qualità della distribuzione ottenuta è molto buona, di solito perfettamente uniforme;
- è possibile ottenere una sequenza identica impostando lo stesso valore di seme.
Questo risulta utile in alcune applicazioni e consente di ottenere un maggiore controllo dei programmi e degli algoritmi eseguiti. Esistono moltissime tecniche per generare numeri pseudocasuali con distribuzioni uniformi, alcune di esse sono anche molto antiche. Il problema è che la maggior parte di queste tecniche non si presta bene ad essere implementata in software o in hardware su sistemi embedded, in quanto richiede operazioni abbastanza complesse (radici quadrate, divisioni, moltiplicazioni, ecc...) per l’estrazione di ogni singolo numero, e può risultare quindi piuttosto lenta. Invece una delle tecniche più semplici, ma al tempo stesso più efficienti ed utilizzate per generare numeri pseudo-casuali fa uso dei “registri a scorrimento con retroazione lineare” (LFSR, Linear Feedback Shift Registers). Si tratta in pratica di normali registri a scorrimento, in cui lo stato futuro è dato da una combinazione lineare dei bit dello stato presente. La combinazione lineare è ottenuta con l’operatore XOR o XNOR. La figura 2 mostra la struttura di un LFSR a 8 bit realizzato con XOR: lo scorrimento avviene verso destra, e ad ogni aggiornamento il bit più significativo riceve la combinazione lineare dei bit presenti in alcune posizioni. Queste posizioni particolari si chiamano “tap”, e devono essere scelte con cura, come spiegato nella figura 2.
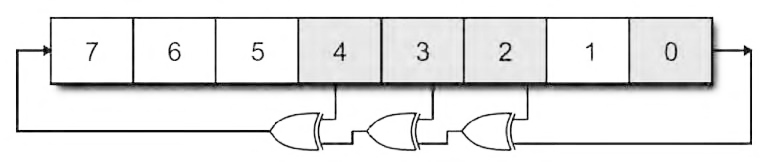
Figura 2: struttura di un LFSR ad 8 bit.
Il funzionamento del circuito è il seguente: si imposta un valore iniziale (diverso da 0), che costituisce il seme e si aggiorna il registro (facendo scorrere i bit di una posizione) ogni volta che si vuole ottenere un nuovo numero casuale. Il circuito funziona praticamente come un contatore, fornendo sempre la stessa sequenza di valori pseudo-casuali, che inizia dal valore dato come seme. Dopo un certo numero di iterazioni, la sequenza ricomincia dall’inizio: la massima lungnhezza della sequenza per un LFSR di lunghezza n bit è 2n-1, ma questo solo se i tap sono stati scelti opportunamente, altrimenti si ottengono delle sequenze più corte. I numeri ottenuti in questo modo sono apparentemente casuali, ed hanno una buona distribuzione uniforme. Una particolarità (a volte utile) è che i numeri estratti non sono mai ripetuti prima che la sequenza ricominci, a meno di non cambiare il seme. Le posizioni dei tap da utilizzare per ottenere la sequenza di lunghezza massima si possono ricavare da apposite tabelle, in cui sono riportati i valori da utilizzare per ogni data lunghezza dell’LFSR (determinare questi valori analiticamente è piuttosto laborioso). In tabella 1 sono riportati alcuni valori comuni (nota: a volte le posizioni dei tap sono numerate da 1 ad n e nel verso opposto rispetto a quello riportato qui).
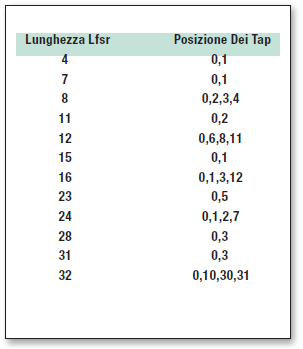
Tabella 1
Una variante dello schema classico dell’LFSR è quello riportato in figura 3, in cui è mostrata la struttura di un “LFSR di Galois”. La differenza sostanziale è che gli XOR sono inseriti nel registro, tra un tap e la posizione successiva, e non nel percorso di feedback. La posizione dei tap è comunque la stessa di prima. Il vantaggio di questa seconda configurazione è che risulta più facile da implementare via software, perché richiede mediamente meno istruzioni, e più veloce via hardware, in quanto i ritardi di propagazione degli XOR non si sommano. L’implementazione di un LFSR nella versione “di Galois” risulta alquanto semplice, sia nella versione software in C che in assembler, sia in hardware su CPLD, FPGA o addirittura logica discreta. Di seguito considereremo questi casi singolarmente con riferimento all’LFSR ad 8 bit di figura 3.

Figura 3: LFSR “di Galois” ad 8 bit.
Nel caso di una codifica in C l’unico aspetto particolare da rilevare è che la variabile che memorizza il contenuto del registro deve essere globale o dichiarata come statica, in modo da mantenere il suo valore (lo stato del registro) durante l’esecuzione del programma. Inoltre la variabile dovrà essere dichiarata di tipo intero unsigned, in modo da evitare inserimenti di bit di segno nelle operazioni di scorrimento. Occorrerà inizializzare il registro con il valore del seme, e poi richiamare la funzione di aggiornamento ogni volta che occorre un nuovo numero casuale. Questa funzione può restituire il valore della variabile, oppure se il registro è stato dichiarato come variabile globale, non sarà necessario passarlo esplicitamene, basterà leggerlo direttamente quando serve (si risparmia qualche accesso alla memoria). Un codice di esempio è riportato nel listato 1.
#include <stdio.h>
// Registro
unsigned char LFSR;
// Funzione di aggiornamento
void NextRand(void);
//—————————
main()
{
int i;
// Inizializzazione (seme)
LFSR=0x01;
for(i=0; i<280; i++) {
printf(“%d: %X”, i, LFSR);
NextRand();
}
}
//—————————
void NextRand(void)
{
unsigned char temp;
temp=0;
if (LFSR&0x01) temp=0x8E;
LFSR=LFSR>>1;
LFSR=LFSR^temp;
}
| Listato 1 |
Il risultato sarà il seguente:
0: 01
1: 8E
2: 47
3: AD
4: D8
5: 6C
6: 36
7: 1B
8: 83
9: CF
10: E9
11: FA
12: 7D
13: B0
14: 58
…
252: 08
253: 04
254: 02
255: 01 <—
256: 8E
257: 47
258: AD
…
La funzione che aggiorna il valore del registro è NextRand. In essa viene testato il bit meno significativo, se questo è uguale a 1 allora gli XOR posti a valle dei tap produrranno un effetto, inoltre il bit meno significativo dovrà essere riportato al più significativo. Se l’LSB è 0 invece ci sarà un semplice shift. Le operazioni di XOR e l’inserimento del bit nell’MSB sono ottenute facendo un XOR con 0x8E (in binario 10001110). Questa operazione ha l’effetto di invertire i bit nelle posizioni corrispondenti agli 1 (e quindi anche aggiungere un 1 all’MSB). Va notato che la posizione dei tre 1 del nibble meno significativo è spostata di uno rispetto alla posizione dei tap perché l’XOR viene fatto dopo lo shift. Il programma visualizza 280 numeri pseudo-casuali, permettendo di osservare che dal 255esimo la sequenza ricomincia. Se si intende provare il programma su un sistema a microcontrollore privo di un dispositivo di visualizzazione, è possibile inviare i numeri ad una UART e visualizzarli su un PC o scriverli in memoria e leggerli con un debugger. L’implementazione in assembler dell’LFSR è ancora più semplice ed efficiente che in C. Nei listati 2 e 3 sono riportati i codici relativi ad un PIC e ad un AVR. L’implementazione hardware dell’LFSR non presenta particolari problemi e può essere fatta riproducendo il circuito di figura 2 o 3 con qualsiasi tecnologia digitale (porte logiche discrete, CPLD, FPGA, etc.), usando un registro a scorrimento e degli XOR esterni, o dei flipflop D e porte XOR dopo i tap. Ci sono due cose interessanti da notare in questo caso: l’implementazione avrà un’occupazione di area piccolissima (in generale n Flip-Flop D + da 1 a 3 porte XOR) e potrà funzionare a frequenze di clock molto elevate.
NextRand CLRW BTFSC LFSR,0 MOVLW 0x8E BCF STATUS,C RRF LFSR,F XORWF LFSR,F RETURN
| Listato 2 |
NextRand: LDI TEMP,0x8E LSR LFSR BRCC Fine EOR LFSR,TEMP Fine RET
| Listato 3 |
DISTRIBUZIONI GAUSSIANE
Se si vuole ottenere una distribuzione pseudo-casuale gaussiana invece che uniforme è possibile utilizzare diverse tecniche. La migliore (come qualità dei campioni ottenibili) consiste nell’utilizzo della trasformata di Box-Muller. Grazie a questa relazione matematica è infatti possibile trasformare una distribuzione uniforme in una gaussiana. Sarebbe sufficiente quindi applicare tale relazione ai campioni generati con un LFSR. Purtroppo le equazioni relative alla trasformata comprendono funzioni difficili da implementare in maniera efficiente, come seno, coseno, logaritmo e radice quadrata. La soluzione più semplice è invece quella di sfruttare il “Teorema del Limite Centrale”, secondo cui (semplificando) sotto certe condizioni la somma di un numero elevato di variabili aleatorie statisticamente indipendenti, tende ad assumere una distribuzione gaussiana al crescere del numero di variabili sommate (questo spiega perché molti processi naturali hanno distribuzioni gaussiane…). In base a questo teorema, se utilizziamo come campioni la somma di N numeri pseudo-casuali generati utilizzando degli LFSR, otteniamo una distribuzione che approssima quella gaussiana. Lo svantaggio di questo approccio è che la distribuzione ottenuta non si estende tra -infinito e +infinito, ma solo tra 0 ed M. Va notato che non si può utilizzare un solo LFSR per generare i campioni da sommare, perché questi non sarebbero statisticamente indipendenti! Occorre usare N LFSR separati (anche della stessa lunghezza) avviati con semi casuali e statisticamente indipendenti. Il listato 4 riporta un frammento di codice utilizzabile per calcolare i campioni (x) di una distribuzione gaussiana, dati un LFSR ed un array che contiene i semi (sd[…]), che poi è usato per mantenere lo stato dei vari registri utilizzati (è un metodo semplice per implementare N LFSR usando una sola routine di aggiornamento).
for(j=0; j<256; j++)
{
for (i=1; i<N; i++)
{
LFSR=sd[i];
NextRand();
x = x + LFSR;
sd[i]=LFSR;
}
x=x/N;
| Listato 4 |
GENERATORI CRITTOGRAFICAMENTE SICURI
Gli approcci considerati fino ad ora sono in assoluto i più utili nelle applicazioni comuni, però come abbiamo visto le sequenze generate hanno un discreto livello di correlazione, e quindi sono facilmente prevedibili. Per gli LFSR ad esempio esiste addirittura un algoritmo esatto per ottenere la struttura del generatore a partire da alcuni campioni raccolti (algoritmo di BerlekampMassey)! Questo rende molti generatori pseudo-casuali non adatti ad essere impiegati in campo crittografico, dove la sicurezza è fondamentale. Questa situazione può essere migliorata, come detto prima variando frequentemente i semi e selezionandoli con un meccanismo casuale autentico (esterno all’algoritmo). Tra gli algoritmi di generazione pseudo-casuali ritenuti migliori e spesso utilizzati nel campo della crittografia meritano una citazione gli algoritmi Mersenne Twister, Fortuna, ISAAC e Blum Blum Shub (BBS). I primi sono un po’ troppo complessi per essere spiegati dettagliatamente qui (e risultano piuttosto pensati da implementare su piccoli sistemi embedded), l’ultimo, che peraltro è uno dei più usati, è relativamente più semplice. Esso si basa sulla seguente relazione: xn+1 = xn 2 mod M in cui un nuovo numero è ottenuto calcolando il quadrato del precedente, modulo M, in cui M è un numero intero ottenuto come prodotto di due numeri primi (in genere grandi). Il termine di partenza x0 è chiaramente il seme. Spesso come risultato non viene considerato il numero in se, ma la sua parità (cioè l’AND bitwise con 1), in modo da ottenere uno stream pseudo-casuale binario. L’implementazione di questo algoritmo non è particolarmente difficoltosa, anche se richiede una moltiplicazione (per calcolare il quadrato) ed una divisione (per calcolare il modulo). Forse il problema più grosso è che la larghezza dei dati può essere decisamente grande (in alcuni casi anche più di 1024bit!).
GENERAZIONE DI NUMERI CASUALI VERI
Per generare dei numeri casuali veri occorre utilizzare un processo aleatorio autentico esterno al programma/ circuito. Sono state proposte moltissime sorgenti di casualità: decadimento radioattivo, diversi tipi di fenomeni quantistici, variazione di luminosità ambientale o di temperatura, instabilità di oscillatori, rumore termico, elettromagnetico o acustico, e perfino variazioni nella velocità di rotazione dei dischi causate da turbolenze locali dell’aria! Per quanto incredibile comunque, quasi nessuno di questi sistemi fornisce risultati soddisfacenti: in genere le distribuzioni di probabilità e di potenza spettrale non sono uniformi (ci sono degli sbilanciamenti a favore di certi valori), c’è un certo margine di prevedibilità, oppure la generazione risulta troppo lenta. Per questo motivo i valori ottenuti con questi metodi devono essere elaborati in qualche modo per potere essere utilizzati in pratica. Considereremo di seguito alcuni metodi semplici da implementare, e le tecniche per correggere eventuali asimmetrie nelle distribuzioni.
MISURE DI TEMPO
Come si può inizializzare un LFSR all’avvio di un’applicazione, in modo che la sequenza non sia sempre la stessa? Una tecnica semplicissima e abbastanza efficace consiste nell’utilizzare come seme una misura di tempo legata a qualche evento esterno. Ad esempio una tecnica molto utilizzata nel campo dei videogame consiste nel misurare il tempo che impiega l’utente per premere il pulsante che avvia la nuova partita. Se il tempo è misurato ad una velocità molto più alta di quella tipica degli eventi tenuti sotto controllo, si può ottenere una buona distribuzione uniforme. Un esempio di codice C per eseguire la misura è riportato nel listato 5.
//… unisgned char cont; //… // Attesa pressione pulsante // (su PORTB.0, attivo alto) cont=0; while(PORTB&0x01) cont++; LFSR=cont; //…
| Listato 5 |
Se nell’applicazione non sono previsti pulsanti o altre forme di interazione con l’utente, oppure se serve generare spesso nuovi numeri casuali o semi, è possibile utilizzare lo stesso identico metodo, ma applicato alla misura del periodo di un oscillatore esterno. L’oscillatore deve avere un periodo sufficientemente grande, ed una pessima stabilità (quindi avere o Q molto basso o meglio essere di tipo RC), quindi essere realizzato con componenti molto sensibili alla temperatura ed alla tensione di alimentazione. Il fatto che il periodo debba essere abbastanza più grande della frequenza di conteggio è dovuto al fatto che normalmente i bit più significativi della misura saranno sempre uguali, mentre quelli più bassi varieranno casualmente. Il valore dovrebbe quindi essere ricavato mettendo assieme un po’ di bit bassi presi da varie misure (per esempio 4 misure da 2 bit).
MISURE DI TENSIONE
Un’altra fonte di casualità è rappresentata dalle misure di tensioni esterne, possibilmente soggette a variazioni ambientali o rumore (sensori di temperatura, di luce, tensione su diodi zener polarizzati inversamente, ecc...). In questo caso occorre utilizzare un convertitore analogico digitale piuttosto preciso (almeno 10 bit) e/o un amplificatore esterno ad alto guadagno e accoppiato in AC. Anche in questo caso una parte dei bit della misura si manterrà stabile, mentre uno o due dei bit meno significativi potranno essere utilizzati per “assemblare” un valore casuale (eventualmente da usare come seme). Quando si utilizza questa tecnica occorre prestare attenzione al fatto che spesso le oscillazioni di tensione che vengono registrate dall’ADC sono causate da un sorgenti periodiche! Un tipico esempio è la tensione di rete a 50Hz, che può essere indotta e misurata facilmente su circuiti ad alta impedenza. Questi fenomeni possono rendere la sequenza più prevedibile o sbilanciare la distribuzione verso certi valori.
MIGLIORAMENTO E CORREZIONE DELLE STATISTICHE
Tutti i metodi “fisici” descritti fino a qui sono affetti da qualche inconveniente che ne altera la distribuzione o aumenta correlazione tra valori generati. Occorre pertanto applicare qualche tipo di elaborazione per migliorarne le caratteristiche. Un’elaborazione molto semplice, ed al tempo stesso efficace per eliminare le asimmetrie nelle distribuzioni (bias o skew), è stata proposta negli anni ‘50 da John Von Neumann. Essa consiste nel considerare lo stream binario generato, raggruppare i dati a blocchi di due bit, ignorare le sequenze 00 ed 11, ed associare a quelle 01 e 10 i valori 0 e 1. In questo modo si ottiene un numero di bit inferiore, ma si può dimostrare che la distribuzione risulta perfettamente riequilibrata. Un’altra tecnica molto comune per eliminare gli squilibri e cancellare gli effetti di interferenze periodiche o deterministiche è quella di utilizzare una funzione di “mixing”. Queste funzioni hanno la proprietà di “scombinare” i valori, in genere spargendoli su un intervallo numerico più grande. In un certo senso gli LFSR alimentati da un seme casuale costituiscono una funzione di mixing, così come le funzioni di hash (SHA, MD5, etc.). Alcune funzioni relativamente semplici da implementare sono gli “scrambler” o le funzioni per il calcolo del CRC (Cyclic Redundancy Check). Queste funzioni non sono altro che degli LFSR dotati di un ingresso per i dati lungo il percorso di reazione. L’uscita può essere presa ovunque, anche su più bit in parallelo (questo permette di ricavare un numero casuale a più bit, fornendo in ingresso solo un bit alla volta). In figura 4 è mostrato lo schema del circuito per il calcolo del CRC a 16 bit (lo stesso usato tra l’altro in molti protocolli di comunicazione).

Figura 4: schema per il calcolo del CRC16.
Come si può vedere la sua struttura è quasi identica a quella degli LFSR di Galois visti in precedenza (i tap non sono quelli dei normali LFSR perché la funzione originaria del circuito è quella di eseguire una divisione di polinomi sul campo di Galois, non generare un conteggio pseudo-casuale). L’implementazione di questo circuito è identica a quella vista in precedenza, l’unica differenza è che in questo caso le operazione sono su due byte. Esistono funzioni CRC con lunghezze diverse, che possono soddisfare diverse esigenze.








Bellissimo articolo.
Questo è un argomento tanto a me caro.
Se ci si pensa bene, un evento casuale o aleatorio non esiste. Esiste solo la “non conoscenza” delle variabili che lo determinano.
Se si conoscessero a priori, tutte le variabili che intervengono nell’evento, con opportune equazioni si arriverebbe a conoscere l’esito finale.
Per esempio, crediamo tutti che il lancio di un dado sia casuale. Ma non è così. Se si sapessero, all’inizio del lancio, le informazioni sul peso del dado, il vento, la forza di spinta, la velocità lineare e angolare, il tipo di superficie di atterraggio, la posizione di partenza del dado, il materiale del dado, eccetera eccetera, si saprebbe in anticipo la faccia che mostrerebbe il dado a fine lancio.
Per i fenomeni cui dietro ci sono comportamenti non lineari ciò non è possibile in quanto le variabili dovrebbero essere conosciute con un numero infinito di cifre.
Poiché invece le cifre sono necessariamente finite i piccoli errori introdotti dalla non conoscenza delle altre cifre provoca errori via via crescenti nel tempo.
L’effetto è noto come “sensibilità alle condizioni iniziali” e fu studiato per primo da Edward Lorenz con un celeberrimo lavoro del 1963.
Lorenz scoprì l’effetto quando osservò che nello sviluppo di un modello meteorologico, con dati di condizione iniziale arrotondati in modo apparentemente irrilevante, non si sarebbero riprodotti i risultati delle analisi con i dati di condizione iniziale non arrotondati. Un piccolo cambiamento nelle condizioni iniziali aveva creato un risultato significativamente diverso.
Questo lavoro è stato male interpretato con la questione dell'”effetto farfalla” che invece sarebbe una non conoscenza di tutte le condizioni iniziali. Non era questo che Lorentz intendeva.