FilterLab è un CAD di Microchip che qualunque appassionato di elettronica può utilizzare per progettare e dimensionare filtri analogici attivi basati su celle ad operazionali. In questo articolo ne illustriamo le principali caratteristiche applicative e le principali funzionalità.

Un filtro è caratterizzato da una precisa banda di trasmissione, i cui limiti sono imposti dal progettista in funzione dell’applicazione. Tale banda è definita attraverso un diagramma di trasmissione (H(s)=|Vu(s)/Vi(s)|). Alla base della progettazione dei filtri vi siano i cosiddetti criteri di approssimazione (Butterworth, Chebyshev, Bessel, Cauer). In questo non ci occuperemo di chip universali per la realizzazione di filtri o di filtri a capacità commutate, ma semplicemente di filtri realizzabili con semplici operazionali e componenti discreti quali resistori e capacità. Simulatori circuitali general-purpose come Orcad Spice o LTSpice possono essere utili per la simulazione del comportamento di filtri attivi di questo tipo tanto da semplificarne enormemente la progettazione.

Esistono altri CAD che possono essere di ausilio alla progettazione di circuiti di questo tipo, alcuni dei quali liberamente scaricabili dalla rete. FilterLab è un cad di questo tipo messo a disposizione da Microchip (www.microchip.com) e particolarmente adatto alla progettazione di filtri attivi multistadio formati da celle ad operazionali.

FilterLab

Le difficoltà che si possono incontrare nella progettazione di un filtro attivo possono essere ridotte notevolmente dall’impiego di un Software come FilterLab. Ciò vale sia per quanti non abbiano una conoscenza teorica e di calcolo sufficiente alla progettazione di questo tipo di circuiti, sia per coloro che, pur conoscendo bene questo tipo di circuiti, necessitano di strumenti che consentano loro di modellare rapidamente e modificare facilmente, anche più volte, un circuito, fino ad ottenerne il comportamento e le prestazioni desiderate, prima ancora che lo stesso venga realizzato. FilterLab non si rivolge a chi vuole utilizzare chip specifici per la realizzazione di filtri come i filtri universali ed è un CAD classificabile come Active Filter Software Design Tool, cioè un cad il cui impiego consente di semplificare enormemente la progettazione dei filtri attivi costruiti intorno ad amplificatori operazionali. Il CAD risponde, in particolare, ad un’esigenza ovvia di progettisti e appassionati di elettronica che hanno a che fare con filtri attivi: generare automaticamente lo schema del circuito di filtro ed i relativi diagrammi di risposta in frequenza a partire dai dati di specifica (figura 1).

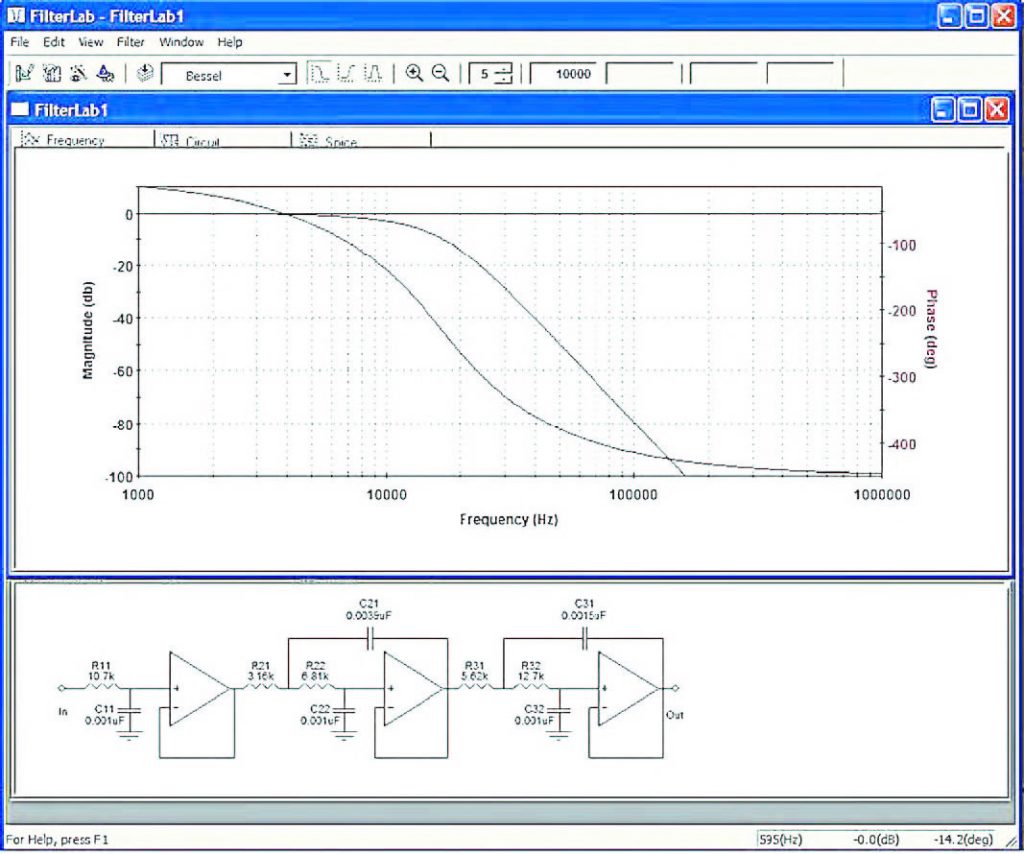
Figura 1: FilterLab genera automaticamente lo schema circuitale del filtro attivo ad operazionali ed i relativi diagrammi di risposta in frequenza a partire dai dati di specifica.

FilterLab consente la progettazione assistita di filtri attivi passa-basso ad operazionali di ordine sino all’ottavo con approssimazione di Chebyshev, Bessel o Butterworth, in un range di frequenze che si stende da 0.1 Hz a 10 MHz e filtri passa-banda e passa-alto con approssimazione di Chebyshev e Butterworth. La tipologia circuitale contemplata dall’implementazione assistita attraverso FilterLab è tipicamente quella di Sallen Key e Multiple Feedback (MFB). L’implementazione dei filtri passa-basso fa riferimento tipicamente sia alla topologia Sallen Key che MFB, quella dei filtri passa-banda alla topologia MFB, mentre quella passa-alto alla topologia Sallen Key. Il CAD consente di generare il modello spice del filtro implementato, modello che può successivamente essere utilizzato in apposite simulazioni spice nel dominio del tempo. Possono anche essere progettati filtri per convertitori analogico-digitali (ADC) fornendo come dati il numero di bit di risoluzione del convertitore ed il sample-rate attraverso un apposito tool integrato (Anti-Aliasing Wizard). Prima di presentare una panoramica generale dell’interfaccia grafica del CAD e di mostrare i passi essenziali che è necessario compiere per eseguire la progettazione di un filtro attivo, riteniamo opportuno riassumere, in una tabella apposita, le principali caratteristiche di questo utile strumento di progetto e di studio (tabella 1).

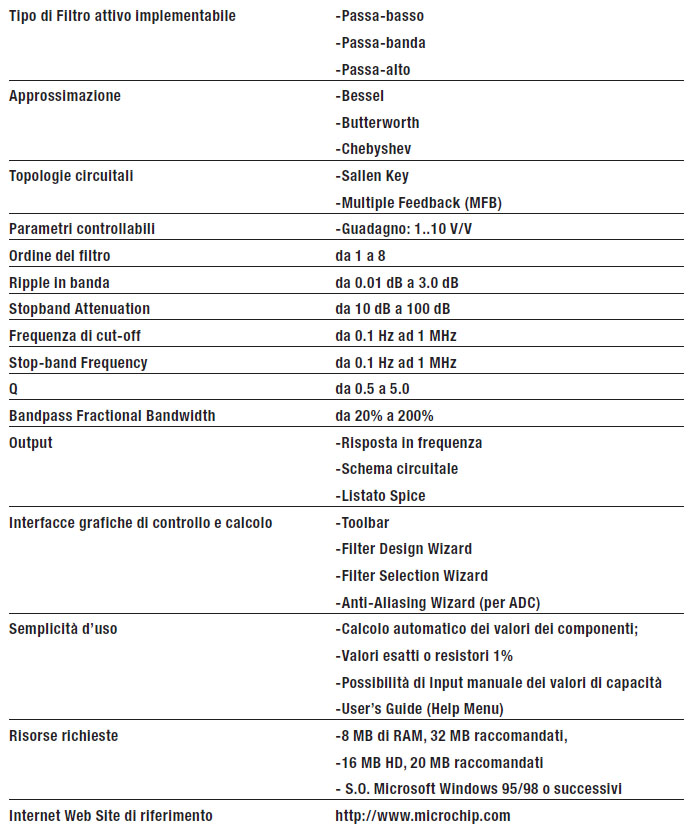
Tabella 1: principali caratteristiche del CAD FilterLab di Microchip.

Creazione e sviluppo di un nuovo progetto

Supposti noti i concetti fondamentali che sono alla base della teoria dei filtri analogici attivi e della loro progettazione, intendiamo illustrare il percorso di progetto che è necessario seguire utilizzando le interfacce grafiche del CAD per giungere alla definizione del circuito ad operazionali che implementa un filtro attivo caratterizzato da una determinata risposta in frequenza. Come accade quando si usa un qualunque software di progettazione, la prima cosa che occorre fare è avere ben chiaro cosa si sta progettando. In questo caso significa aver definito preventivamente che tipo di filtro attivo si intende realizzare e quale risposta in frequenza questo debba presentare. A questo punto è necessario avviare la creazione di un nuovo progetto (File/New) e introdurre i dati di specifica. Tale operazione può essere avviata in due modi distinti ma equivalenti. Il primo consiste nell’impiego del comando Filter/Design (figura 2A), il secondo in quello del pulsante Design Filter disponibile nell’apposita toolbar messa a disposizione dall’interfaccia grafica (figura 2B).

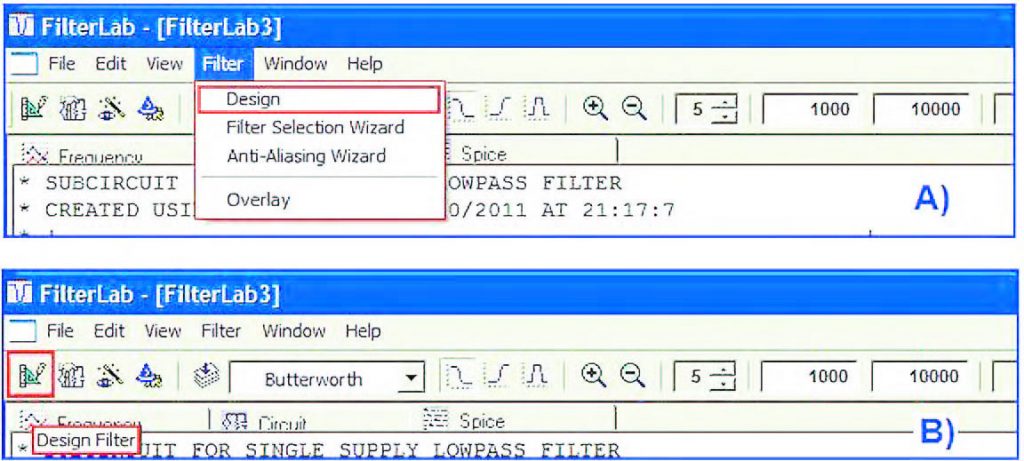
Figura 2: per avviare un nuovo progetto e introdurre i dati di specifica di quest’ultimo, è necessario utilizzare il comando Filter/Design (A) o in modo equivalente agire attraverso il pulsante “Design Filter” (B).

In ogni caso, il comando rende immediatamente disponibile un form che consente di impostare le caratteristiche principali del filtro che si intende progettare e dimensionare. I dati che vengono impostati all’interno di questo form consentono di imporre il tipo di approssimazione, il tipo di selettività del filtro ed alcune caratteristiche circuitali generali. All’interno del form sono infatti disponibili tre diversi tab, ciascuno dei quali preposto all’impostazione di una parte dei suddetti dati. Il tab “Filter Specification” (figura 3) consente di definire il tipo di approssimazione (Butterworth, Bessel o Chebyshev) ed il tipo di filtro che si intende progettare da un punto di vista di selettività (passa-basso, passa-alto o passa-banda).

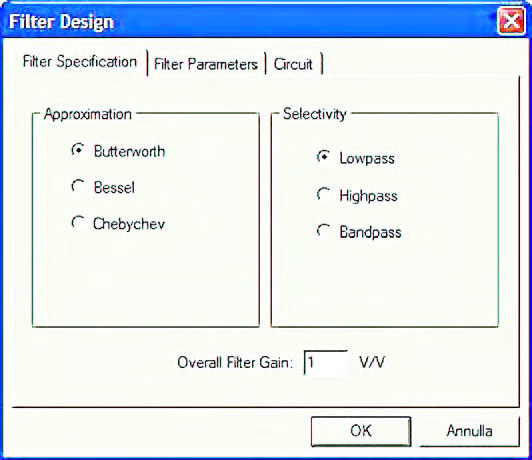
Figura 3: il tipo di approssimazione viene impostato all’interno della pagina “Filter Specification” accessibile attraverso l’omonimo tab del form “Filter Design”.

Trattandosi di filtri attivi è possibile impostare un fattore di guadagno che può presentare come massimo valore 10 V/V (figura 3). È interessante osservare come l’approssimazione di Bessel consenta di impostare, come tipologia di filtro, la sola tipologia passa-basso (figura 4).

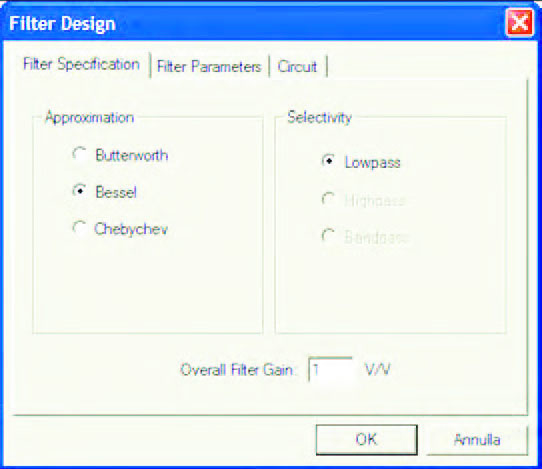
Figura 4: l’approssimazione di Bessel consente la progettazione di soli filtri passa-basso.

Le specifiche di un filtro possono essere espresse attraverso un cosiddetto diagramma di trasmissione che riporta sulle ascisse le  frequenze o le pulsazioni, ed in ordinata il rapporto Vu/Vi. L’ascissa, cioè l’asse delle frequenze, è così suddivisa in bande e tra queste deve essere possibile distinguere, in particolare, la banda passante (BP) e le bande di transizione (BT). In ogni caso, mentre l’analisi di un filtro consiste nella descrizione del suo comportamento in frequenza mediante funzione di trasferimento, la sintesi consiste nella sua definizione a partire dalle caratteristiche di trasmissione, a partire cioè dalla sua risposta in frequenza. Da questo punto di vista è possibile affermare che FilterLab è soprattutto uno strumento di sintesi. La pendenza della risposta nelle zone di transizione è, inoltre, strettamente legata all’ordine del filtro, cosa che, a sua volta, ha implicazioni sul numero di celle che lo compongono e quindi, indirettamente, sulla complessità circuitale dello stesso. La sintesi teorica di un filtro, sia esso passivo oppure attivo, prevede l’impiego di un cosiddetto LPF equivalente, caratterizzato da una caratteristica normalizzata da cui successivamente si ricava il filtro desiderato ed effettivamente rispondente ai dati di specifica. Nella sintesi possono poi essere presi in considerazione criteri di approssimazione che ottimizzano la caratteristica di trasmissione in una delle bande di frequenza. Da ciò discende la necessità, anche all’interno dei cad di ausilio alla progettazione dei filtri, di definire il tipo di approssimazione scegliendo appunto tra:

• approssimazione di Butterworth: ottimizza la caratteristica di trasmissione nella banda passante presentando una risposta senza oscillazioni e con la maggior piattezza possibile;
• approssimazione di Chebyshev: ottimizza la caratteristica di trasmissione nella banda di transizione, presentando un’elevata pendenza a scapito di un certo ripple di ampiezza nella banda passante;
• approssimazione di Bessel: si riferisce esclusivamente ai filtri passa-basso. All’uscita di un filtro LPF, normalmente le forme d’onda che si presentano all’interno della banda passante sono caratterizzate da una distorsione di fase poiché differenti frequenze subiscono ritardi differenti nell’attraversamento del filtro. Un filtro di Bessel consente di ottenere un tempo di ritardo di fase più costante all’interno della banda. All’interno della pagina “Filter Parameters”, accessibile attraverso l’omonimo tab all’interno del form “Filter Design”, è possibile impostare le caratteristiche che definiscono la risposta in frequenza del filtro. A seconda del tipo di filtro e della selettività precedentemente impostata è possibile introdurre i valori dei seguenti parametri:
  • passband attenuation (dB);
  • stopband attenuation (dB);
  • passband lower frequency;
  • passband upper frequency
  • stopband lower frequency;
  • stopband upper

In figura 5 è riportato il significato di questi parametri per un filtro passabanda, mentre in figura 6 è riportata la pagina “Filter Parameters” del form Filter Design all’interno della quale vanno inseriti i valori dei parametri suddetti.

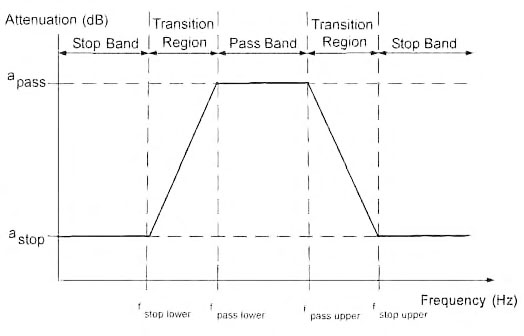
Figura 5: parametri che definiscono la selettività di un filtro passa-banda.

Tra le opzioni possibili, lasciate a discrezione dell’utente, vi è la possibilità di impostare l’ordine del filtro (figura 6, check-box “Force Filter Order”).

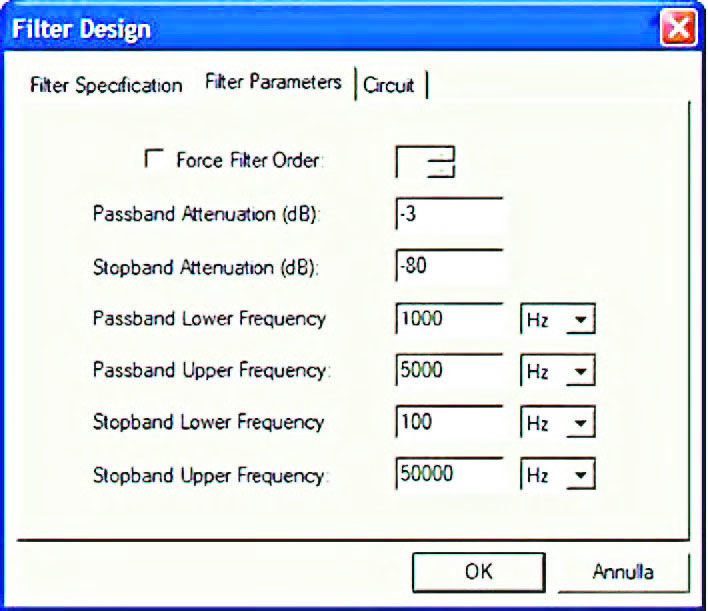
Figura 6: pagina “Filter Parameters” del form Filter Design. All’interno di questa pagina vanno inseriti i valori dei parametri che definiscono le caratteristiche di selettività del filtro.

In questo caso l’utente è chiamato a specificare i valori Pass Band Attenuation e Pass Band frequency. Il cad calcola automaticamente i valori Stop Band Attenuation e Stop Band frequency essendo questi legati direttamente all’ordine del filtro già imposto (figura 7).

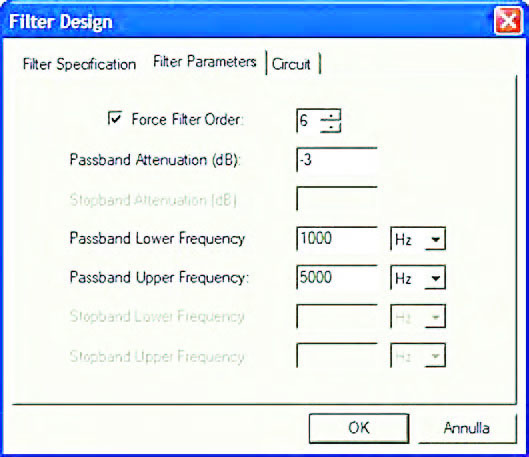
Figura 7: l’utente può imporre l’ordine del filtro attraverso il check-box “Force Filter Order” della pagina Filter Parameters del form Filer Design. Alcune dei parametri caratteristici che definiscono la selettività sono in questo caso determinate automaticamente dal CAD.

Nel caso in cui il suddetto check-box non venga selezionato, è l’utente a definire direttamente i valori di attenuazione ed i valori caratteristici di frequenza. Il cad in questo caso esegue un’operazione opposta alla precedente: calcola cioè l’ordine del filtro in funzione dell’attenuazione e dei valori di frequenza specificati dall’utente. Il fatto di poter procedere in entrambi i modi rende le operazioni certamente più agevoli ed il cad più flessibile. Completata l’impostazione di tutti i parametri che definiscono le caratteristiche di selettività del filtro attivo, è possibile passare alla generazione dello schema elettrico del filtro stesso. Tale operazione viene avviata attraverso il tab “Circuit” presente all’interno del form “Filter Design” (figura 8B) oppure attraverso il pulsante “Design Circuit” (figura 8A).

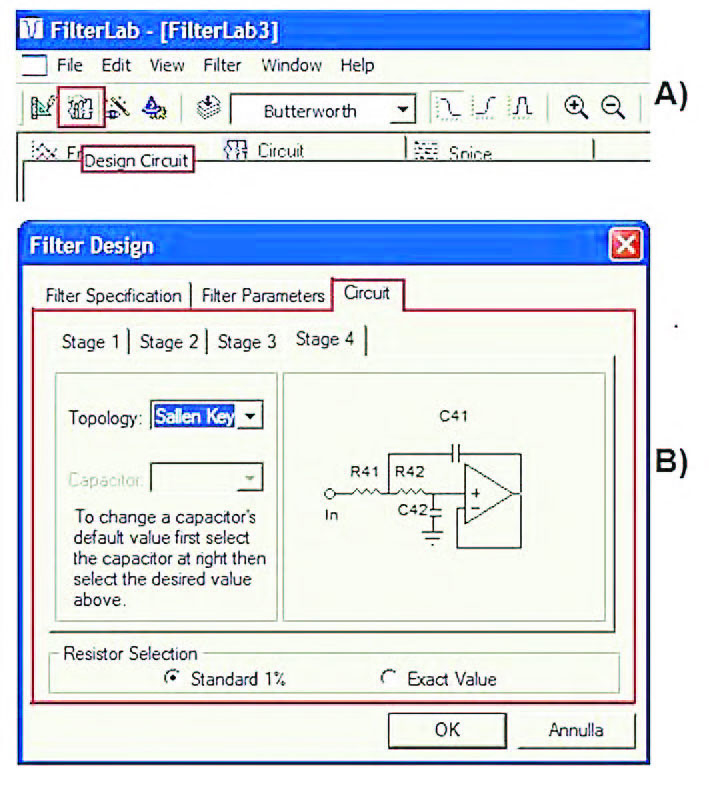
Figura 8: attraverso il tab “Circuit” del Form Filter Design (B) oppure attraverso il pulsante “Design Circuit” (A) è possibile avviare la generazione dello schema elettrico del filtro i cui parametri caratteristici sono stati precedentemente definiti.

Attraverso la pagina restituita dal suddetto tab, l’utente può controllare l’impostazione dei singoli stadi che compongono il filtro attivo ed il cui numero dipende dall’ordine dello stesso filtro e quindi, indirettamente, dalla sua maggiore o minore selettività nelle zone di transizione. Ciascuno degli stadi interessati può essere in questa fase impostato come stadio Sallen-Key oppure come stadio MFB (figura 8). I componenti ohmici che compaiono all’interno dei singoli stadi possono essere impostati su valori standard con precisione 1%, nel caso in cui si desideri orientare maggiormente il circuito stesso all’implementazione fisica che seguirà, oppure su valori esatti (figura 7B si notino i radio-button “Standard 1%” ed “Exact Value”). Tra le opzioni possibili lasciate a discrezione dell’utente, vi è la possibilità di impostare l’ordine del filtro (figura 6, check-box “Force Filter Order”). In questo caso l’utente è chiamato a specificare i valori di frequenza Pass Band Attenuation e Pass Band frequency. Il cad calcola automaticamente i valori Stop Band Attenuation e Stop Band frequency, essendo questi legati direttamente all’ordine stesso del filtro, già precedentemente definito (figura 7). Nel caso in cui il suddetto check-box non venga selezionato, è l’utente a definire direttamente l’attenuazione a valori caratteristici di frequenza. Il cad in questo caso esegue un’operazione opposta alla precedente: calcola cioè l’ordine del filtro in funzione dell’attenuazione e dei valori di frequenza specificati dall’utente. Il fatto di poter procedere in entrambi i modi rende ancora una volte le operazioni più agevoli ed il cad più flessibile. Alla fine del processo di progetto l’utente dispone di tre finestre che riassumono i risultati: la finestra “Frequency” che riporta la risposta in frequenza del filtro, la finestra “Circuit” (figura 9 e figura 10) che riporta lo schema elettrico del circuito e la finestra “Spice” che riporta il listato spice dello stesso circuito.

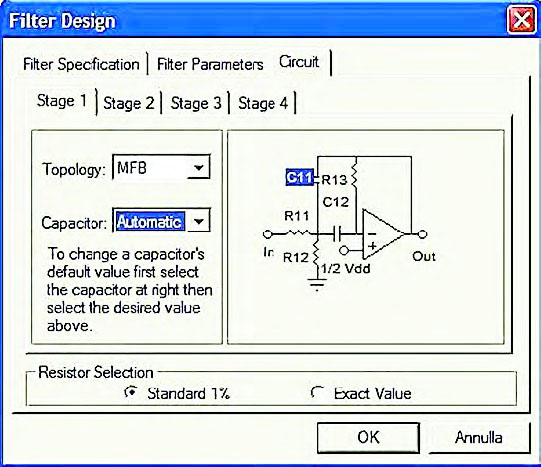
Figura 9: all’interno del tab “Circuit” è possibile modificare i valori delle capacità che compaiono sui singoli stadi del filtro rispetto a quelli proposti automaticamente dal cad. FilterLabmodifica automaticamente i valori ohmici dei resistori e delle altre capacità al fine di garantire la desiderata risposta del filtro.

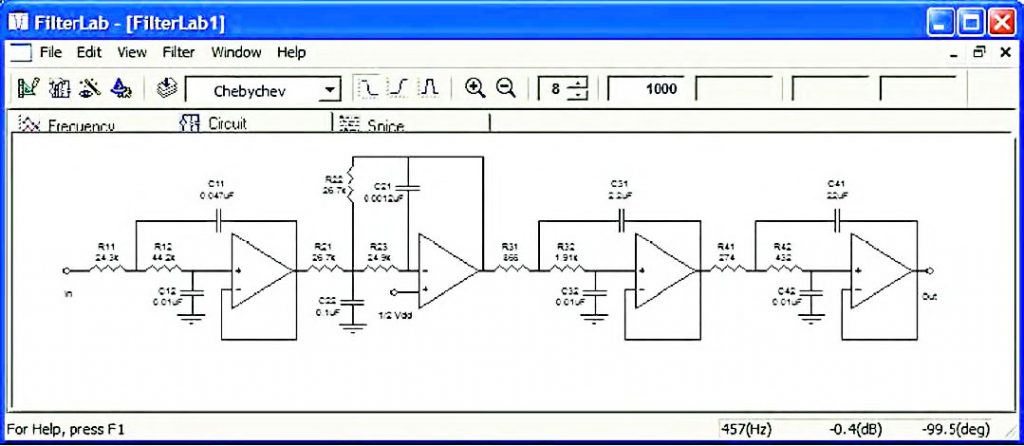
Figura 10: alla fine del percorso di progetto il CAD restituisce il circuito completo di tutti gli stadi attivi componenti il filtro.

A queste finestre è possibile accedere rispettivamente attraverso il tab “Frequency” evidenziato in rosso in figura 11, il tab “Circuit” evidenziato in verde ed il tab “Spice” evidenziato in blu nella stessa figura. Particolarmente importante è la Frequency View (figura 11) che riporta la risposta in frequenza del filtro. L’asse, la cui scala è riportata a sinistra, riporta l’attenuazione del filtro. L’impostazione di default riporta una scala compresa tra +10 dB e -80 dB. L’asse di destra riporta invece la fase della risposta del filtro in gradi o in radianti. Agendo sulla finestra Frequency view, attraverso il pulsante destro del mouse è possibile far comparire il pop-up Menu Phase/Group Delay. Agendo attraverso il comando “Save as Jpeg” è quindi possibile salvare la risposta del filtro come immagine jpeg.

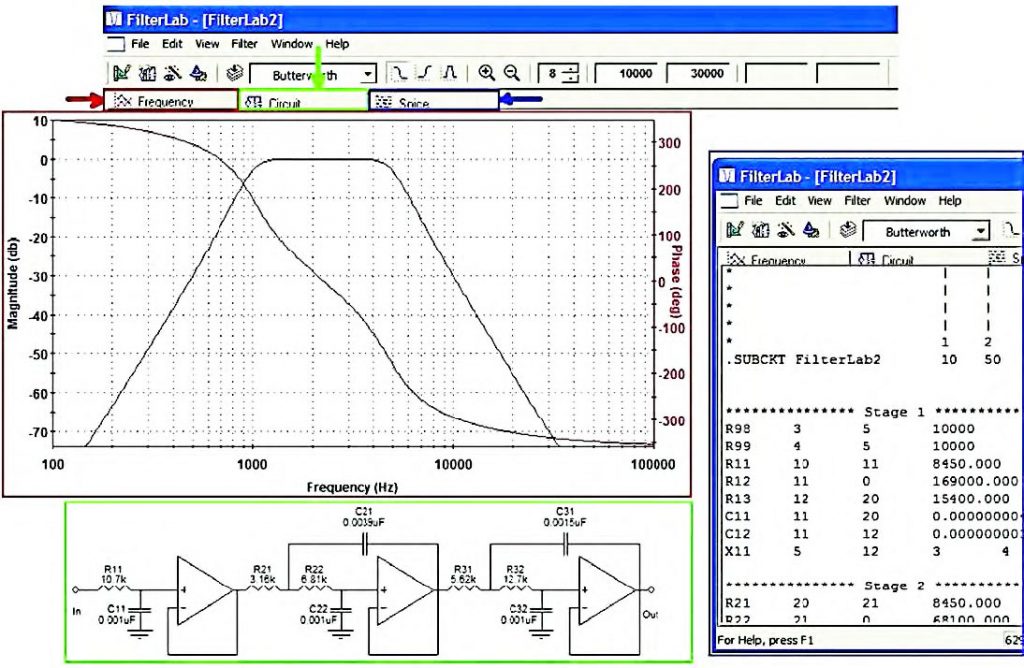
Figura 11: risultati della progettazione (tab Frequency, Circuit e Spice).

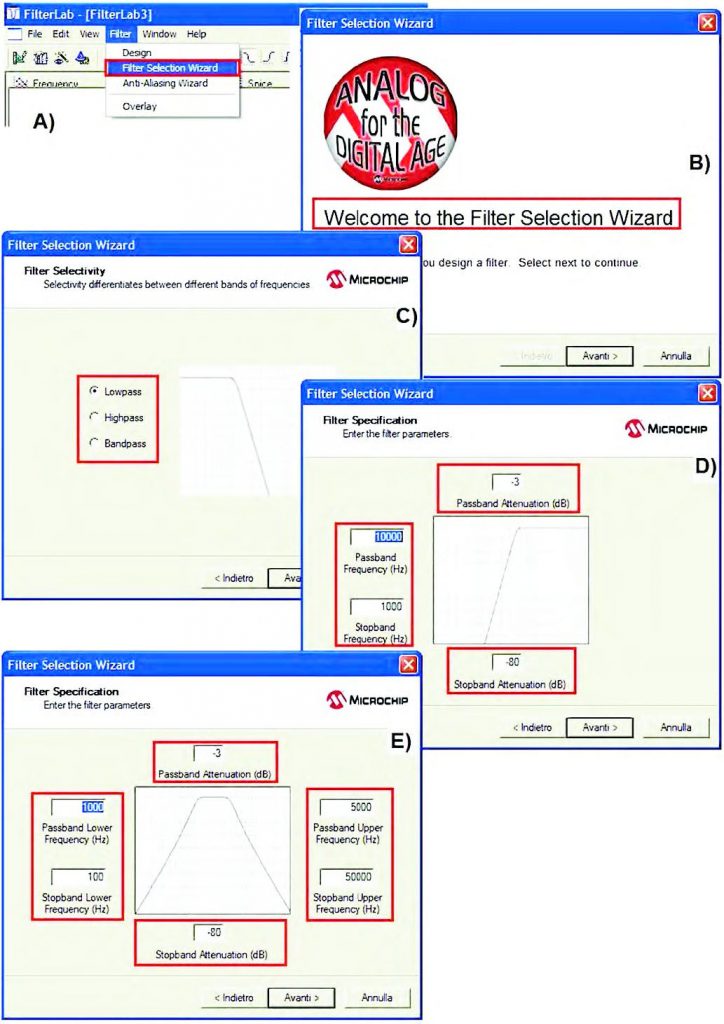
Figura 12: fillter Selection Wizard. A,B)- Accesso alle  funzionalità; C)-Scelta del tipo di filtro (Selectivity); D,E)- Impostazione delle frequenze caratteristiche del filtro (Filter Specification).

Filter Selection Wizard

Nel precedente paragrafo abbiamo illustrato il processo generale che porta alla definizione dei parametri caratteristici del filtro. Il comando “Filter Selection Wizard” (figura 11) consente di introdurre tali parametri in maniera tale da definire la selettività dello stesso filtro attraverso una tabella riassuntiva che mostra ordine, banda e attenuazione del filtro stesso. All’interno del form Filter Selectivity è possibile impostare i dati di selettività, mentre all’interno del form Filter Specification è possibile inserire i parametri caratteristici del filtro tra i quali attenuazione e frequenze caratteristiche. Per un filtro passa-basso o per un passa-alto si tratta di:

• Pass Band Attenuation: attenuazione, cioè variazione, del modulo della risposta in banda. I valori consentiti sono compresi tra 0.01 dB e -3 dB;
• Stop Band Attenuation: valore di attenuazione, compresa tra -10 dB e - 100 dB;
• Pass Band Frequency: punto in cui inizia la banda passante. Il range consentito è quello compreso tra 0.1 Hz e 1,000,000 Hz;
• Stop Band Frequency.

Nel caso in cui vengano introdotti per i diversi parametri valori differenti rispetto ai range consentiti, il cad genera la segnalazione di un messaggio di errore che guida l’utente alla necessaria correzione (figura 12). Analogamente, nel caso in cui si progetti un filtro passa banda, è necessario introdurre i valori di:

• Passband Attenuation;
• Stopband Attenuation;
• Passband Lower Frequency;
• Stopband Lower Frequency;
• Stopband Upper Frequency;
• Passband Upper

Figura 13: nel caso in cui i valori impostati all’interno del form “File Selection wizard” non siano compresi nei range dei valori ammessi il cad fornisce una segnalazione di errore che guida l’utente alla comprensione dello stesso e quindi alla sua immediata correzione.

All’impostazione dei dati all’interno del form Filter Specification segue il form Filter Approximation che propone all’utente il riassunto delle impostazioni effettuate e mostra l’ordine calcolato (figura 14).

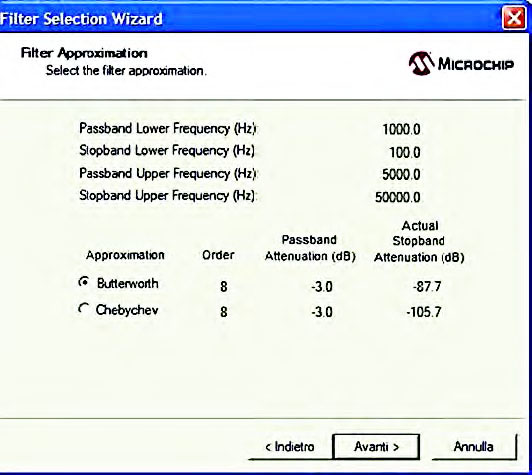
Figura 14: form “Filter Approximation” del percorso di prgetto Filter Selection Wizard.

L’utente deve a questo punto, attraverso l’apposito radio-button presente all’interno di detto form, scegliere il tipo di approssimazione tra le opzioni proposte (Butterworth e Chebychev). A questa fase segue la comparsa del form “Completing the Filter” che riassume tutte le impostazioni effettuate. Giunti a questo punto è sufficiente premere il pulsante Finish per dare il via alla vera e propria implementazione circuitale del filtro (figura 15).

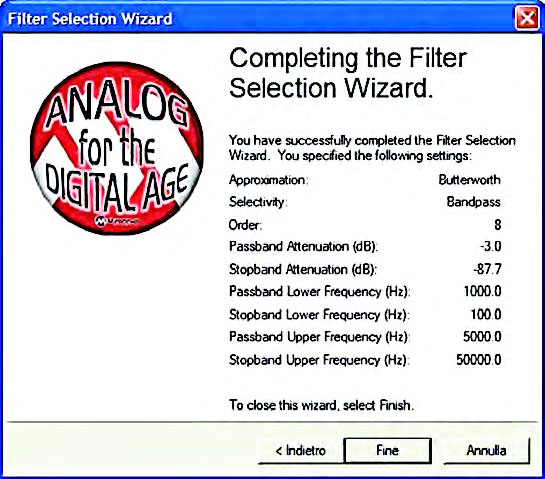
Figura 15: form “Completing the Filter” del percorso di progetto Filter Selection Wizard.

Anti-Aliasing Wizard

FilterLab integra un Anti-Aliasing Wizard, ovvero un percorso di progetto in grado di assistere l’utente nella progettazione di un filtro passa-basso finalizzato all’impiego in un convertitore A/D (figura 16). Il suo impiego prevede, nell’ordine, l’introduzione dei valori di banda, frequenza di campionamento (che deve risultare maggiore o uguale al doppio della frequenza di cut-off), risoluzione (compreso tra 8 e 24 bit) e rapporto segnale-rumore del convertitore A/D (figura 16).

Figura 16: avvio dell’ Anti-Aliasing Wizard.

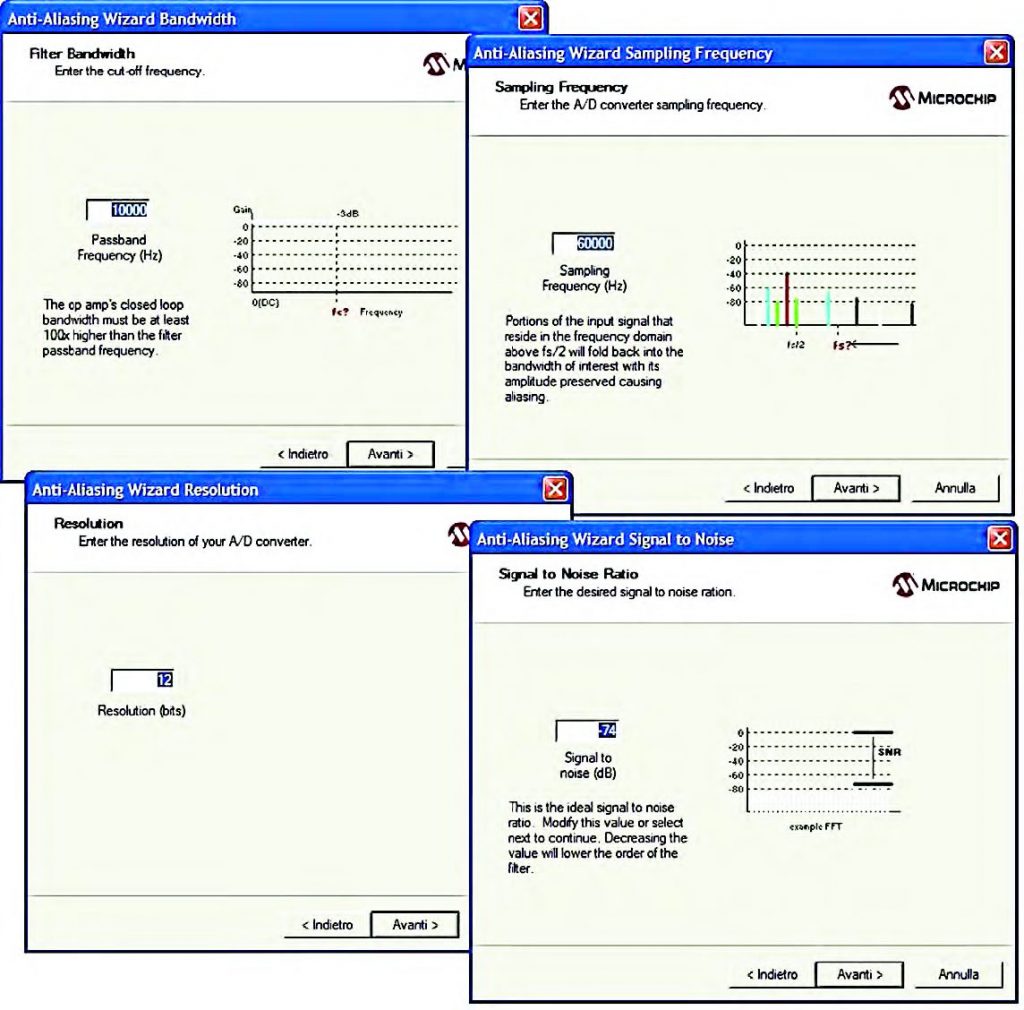
Figura 17: il percorso Anti Aliasing Wizard prevede, nell’ordine, l’introduzione dei valori di banda, frequenza di campionamento, risoluzione e rapporto segnale-rumore del convertitore A/D.

La frequenza di cut-off definisce la banda del filtro anti-aliasing (figura 17). Il range di frequenza è limitato tra 0.1 e 1 MHz. Nel caso in cui venga inserito un valore esterno a questo range, l’operazione determina la generazione di un messaggio di errore (figura 13) che invita l’utente alla correzione. Il rapporto segnale-rumore, come noto, è direttamente legato al numero di bit utilizzati per la conversione (valore di default 6.02 * bits + 1.76). A questo parametro è legata anche la selettività e, quindi, l’ordine del filtro. Al decrescere di questo parametro corrisponde la diminuzione dell’ordine del filtro, mentre al crescere di questo corrisponde un aumento dell’ordine del filtro. Il percorso di calcolo si conclude con il form di figura 18 all’interno del quale viene specificato il tipo di approssimazione che va scelto tra le due opzioni Butterworth e Chebyshev e che riassume i parametri caratteristici dello stesso filtro.

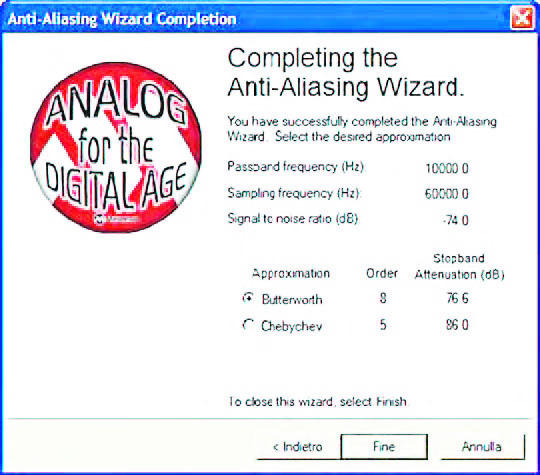
Figura 18: il percorso Anti-Aliasing Wizard si conclude con la scelta del tipo di approssimazione (opzioni possibili: Butterworth e Chebyshev).

La toolbar ed i menu di FilterLab

Nei paragrafi che si sono susseguiti fino a questo momento abbiamo illustrato le caratteristiche del Cad e le linee generali delle operazioni da eseguire per la progettazione di  un  filtro analogico ad operazionali. Nei paragrafi che seguono intendiamo dare un’occhiata più attenta rispettivamente alla toolbar ed ai menu messi a disposizione dal cad. Ne diamo una rapida descrizione, senza soffermarci eccessivamente sull’operatività che è stata già sufficientemente esposta. La toolbar dispone di una serie di pulsanti shortcut degli stessi comandi disponibili all’interno dei menu (figura 19).

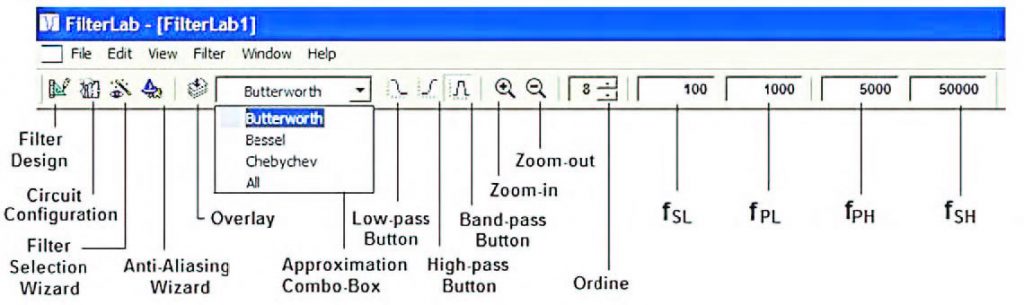
Figura 19: dettaglio della toolbar do FilterLab

In particolare, nella suddetta toolbar si notano i pulsanti Filter Design, Circuit Configuration, Filter Selection Wizard ed Anti-Aliasing Wizard, l’Approximation Combo Box, all’interno della quale è possibile impostare il tipo di approssimazione, i pulsanti di impostazione del tipo di filtro (Low-pass, Bandpass ed High-pass), i pulsanti di zoom, quelli per l’impostazione dell’ordine del filtro e le aree per l’impostazione delle frequenze che caratterizzano il filtro (frequency text box). L’Approximation combo box si presenta inoltre con aspetto differente a seconda del tipo di filtro che si intende progettare. In particolare, l’approssimazione di Bessel è disponibile unicamente per filtri passa-basso. Stessa cosa accade per le frequency text box il cui numero cambia a seconda del tipo di filtro. In figura 20 è invece riportato un esploso abbastanza dettagliato dei menu che il cad integra al suo interno. La barra dei menu integra i seguenti menu a tendina: File, Edit ed Help come è tipico, del resto, di quasi tutti gli applicativi che ciascuno di noi utilizza comunemente sul proprio PC e menu specifici e tipici del Cad come View, Filter e Window i cui comandi e le cui funzionalità sono maggiormente legati alla progettazione vera e propria del filtro. Qualche attenzione in particolare merita il menu Filter il quale consente di accedere alle funzioni di progettazione del filtro. Esso integra infatti i comandi Design, Filter Selection Wizard ed Antialiasing Wizard, le cui funzioni sono accessibili anche attraverso gli appositi pulsanti della toolbar.

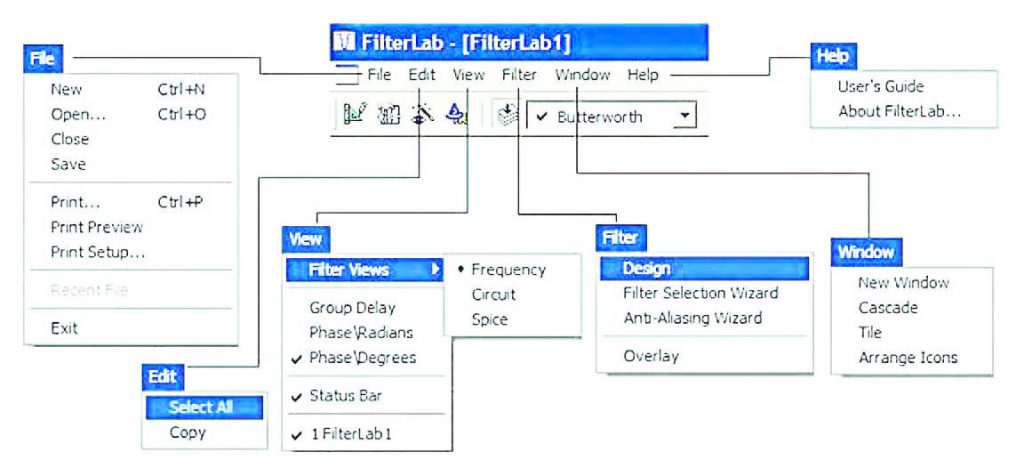
Figura 20: barra dei Menu.

Appendice: la risposta in frequenza di un filtro

Nei precedenti paragrafi abbiamo mostrato quali siano le caratteristiche di FiletrLab e le fasi operative che consentono di progettare con il suo ausilio un filtro analogico attivo basato sull’impiego di amplificatori operazionali. Nel corso dell’esposizione non ci siamo preoccupati degli aspetti teorici che sono alla base della modellizzazione di questo tipo di circuiti e delle relative risposte in frequenza. Il primo dei due aspetti è giustificato dal fatto che il cad serve proprio per evitare di dover conoscere in maniera specifica la teoria di calcolo dei filtri elettronici. Per quanto riguarda il secondo, sebbene senza addentrarci in dettagli eccessivi, riteniamo opportuno riportare almeno la rappresentazione generale della risposta in frequenza dei diversi filtri indicandone i principali parametri caratteristici. In figura 21 sono sintetizzate in particolare tutte le caratteristiche della risposta in frequenza di un filtro passa-basso.

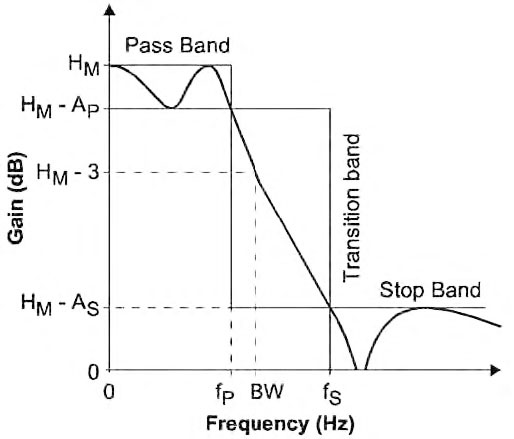
Figura 21: tipica risposta di un filtro passa-basso e relativi parametri caratteristici.

La risposta nominale del filtro è compresa all’interno di tre regioni (pass band, transition band e stop band). La Pass Band è caratterizzata da un valore di guadagno massimo HM(dB), un’attenuazione in banda A(dB) rispetto ad HM e quindi da un Ripple/Massima Attenuazione (dB) in banda AP, da una banda passante (Hz) fP e da una banda BW a -3dB. La Stop Band è invece caratterizzata dalle frequenze fS (Stop Band Edge Frequency-Hz), dal minimo valore di attenuazione nella Stop Band AS(dB). Il guadagno G corrisponde al guadagno in continua per cui G=HM per i filtri passa-basso con approssimazione di Bessel, Butterworth and Chebyshev (n = 1, 3, 5, 7) mentre G=HM-AP per filtri passa-basso con approssimazione di Chebyshev (n = 2, 4, 6, 8). In figura 22 sono riportati i diagrammi in frequenza di un filtro passa-basso per i diversi tipi di approssimazione al variare dell’ordine dello stesso filtro.

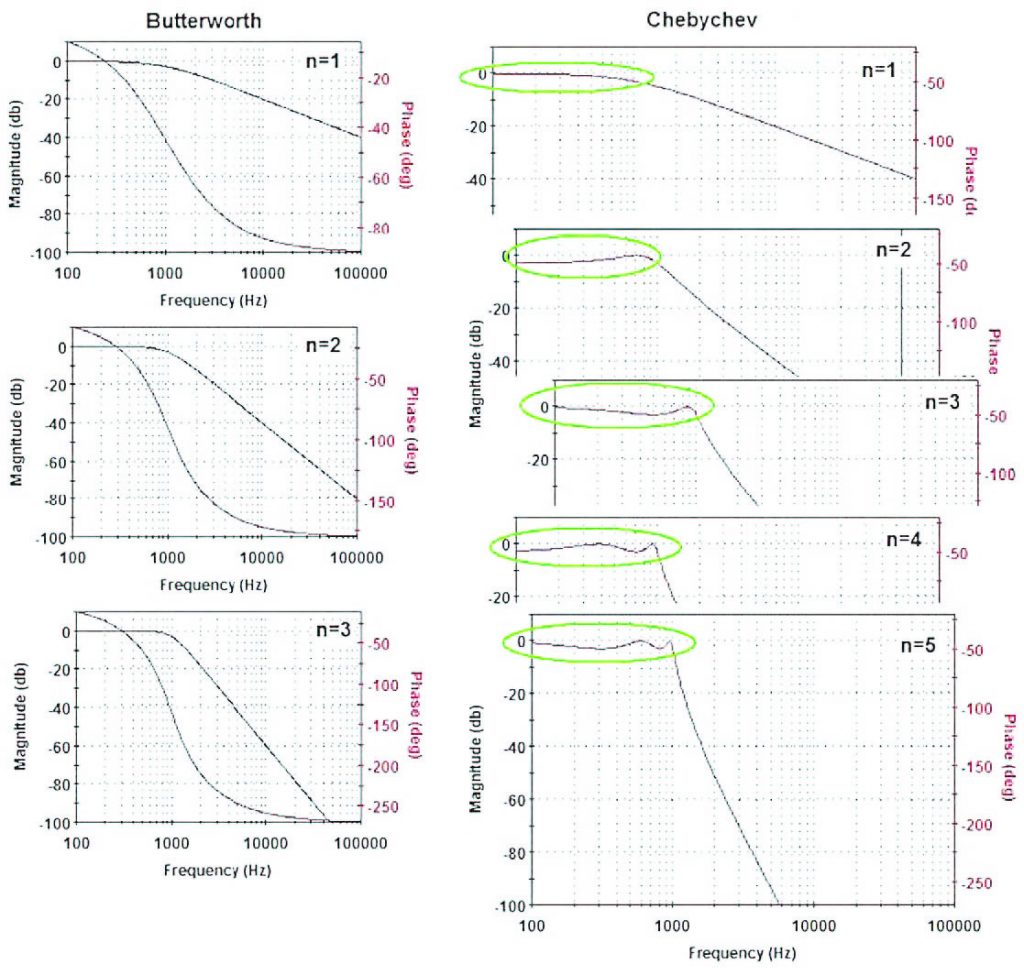
Figura 22: diagrammi in frequenza per un filtro passa-basso per le approssimazione rispettivamente di Butterworth e Chebyshev al variare dell’ordine.

Un’osservazione attenta di questi è sufficiente per osservare quanto appena detto sul guadagno in continua del filtro. La risposta di un filtro passa-banda è invece rappresentabile in generale come in figura 23.

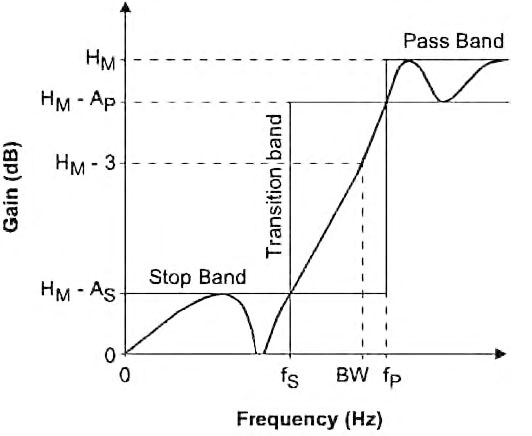
Figura 23: tipica risposta di un filtro passa-banda e relativi parametri caratteristici.

La risposta del filtro è contenuta pertanto all’interno delle cinque regioni mostrate all’interno della figura (una banda passante, due bande di transizione e due stop band). Il guadagno G corrisponde al guadagno alla frequenza f0 di centro banda per cui, come è semplice verificare attraverso alcune semplici simulazioni G=HM per le approssimazioni di Butterworth e Chebyshev con n = 2, 6 ed HM-AP per l’approssimazione di Chebyshev con n = 4, 8. Analogamente, per un filtro passa-alto, la risposta in ampiezza assume la forma generale mostrata in figura 24.

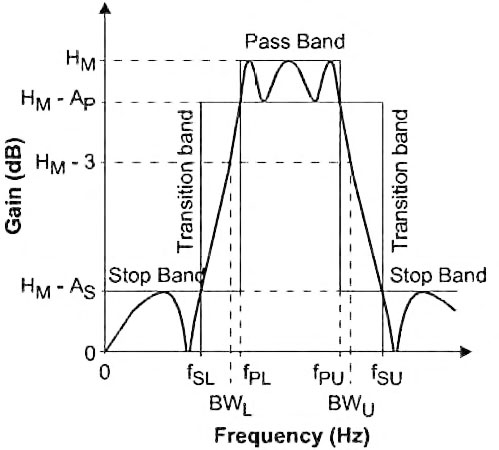
Figura 24: tipica risposta di un filtro passa-alto e relativi parametri caratteristici.

La risposta nominale del filtro è quindi in generale definita dalle seguenti tre regioni: banda passante, banda di transizione e stop band. Si distinguono pertanto la frequenza fP (Pass Band FrequencyHz), la banda B a -3 dB, il massimo guadagno in banda HM(dB), l’attenuazione A relativa al valore massimo HM (dB), il massimo valore di ripple/attenuazione AP, la frequenza fS(Hz) che definisce superiormente la Stop Band, il minimo valore di attenuazione AS(dB) nella Stop Band. Il guadagno G corrisponde in questo caso al guadagno in alta frequenza per cui, come è facile verificare con alcune simulazioni, esso risulta pari a G=HM per l’approssimazione di Butterworth e Chebyshev con n = 1, 3, 5, 7 e G=HM-AP per l’approssimazione di Chebyshev con n = 2, 4, 6, 8.

Cenni alla scelta dell’operazionale

I filtri che è possibile progettare  attraverso FilterLab sono filtri attivi costruiti intorno ad amplificatori operazionali. La scelta dell’operazionale ovviamente presenta anch’essa una sua importanza. Quando si sceglie un operazionale per realizzare un filtro, infatti, sebbene la sua risposta dipenda fortemente dalla tipologia circuitale e dai componenti che circondano lo stesso operazionale, è necessario porre una certa attenzione anche al tipo di operazionale. In particolare, è importante, come è ovvio immaginare, che esso sia sufficientemente veloce tanto da consentire la realizzazione del filtro nella banda desiderata. Per questo motivo è necessario che l’operazionale presenti il necessario prodotto guadagno-banda. Inoltre il filtro dovendo spesso essere in grado di rispondere a segnali anche piuttosto ampi è necessario che presenti un sufficiente valore di SR (Slew Rate). I circuiti di filtro progettati con FiletLab devono pertanto utilizzare operazionali aventi prestazioni adeguate, soprattutto se si desidera operare in bande a frequenze abbastanza elevate. Tale osservazione è, del resto, di carattere generale e riguarda la progettazione di questi circuiti indipendentemente dagli strumenti cad impiegati.

Conclusioni

Nel presente articolo abbiamo illustrato le caratteristiche del Cad FilterLab di Microchip. Abbiamo quindi mostrato come il cad possa essere facilmente utilizzato nella progettazione di filtri analogici attivi ad operazionali con selettività passa-basso, passa-alto e passa-banda basati sui metodi di approssimazione di Butterworth, Chebyshev e Bessel. L’interfaccia estremamente semplice consente una interattività immediata e rende il cad di semplice impiego, anche da parte di chi non abbia una conoscenza specifica della teoria dei filtri. La possibilità di avere a disposizione, alla fine della progettazione del filtro, i diagrammi di risposta in frequenza, lo schema elettrico ed il listato Spice di quest’ultimo, rende il cad sufficientemente completo e flessibile. In ogni caso, l’operatività di FilterLab prevede due o tre fasi di lavoro a seconda dei casi. I form Filter Design e Filter Selection Wizard consentono di inserire i dati di specifica per lo sviluppo del progettato cui segue la generazione della risposta in frequenza e dello schema elettrico del filtro. A chi intende prendere visione diretta delle potenzialità e della semplicità di impiego del cad consigliamo di effettuarne il download direttamente da sito di Microchip, di installarlo sul proprio PC e di provare ad utilizzarlo per realizzare qualche filtro analogico attivo avente specifiche caratteristiche di selettività. Anche gli studenti di elettronica potranno trarre beneficio dal suo impiego poiché potranno utilizzarlo come vero e proprio laboratorio didattico sull’argomento. Nella sezione “Riferimenti bibliografici” sono riportati i principali riferimenti per il download del Cad e per il download della documentazione necessaria al suo studio ed al suo corretto impiego che rimane in ogni caso estremamente semplice ed intuitivo.

Ti potrebbe interessare anche:

LPC1758 ARM CORTEX-M3

PLC, Arduino o Raspberry Pi? Come scegliere la giusta soluzione

Lo stack TCP/IP di Microchip