
Il controllo e l’azionamento delle parti in movimento è da sempre stata una delle branche più accattivanti a cui un appassionato di elettronica possa avvicinarsi. Nell’articolo che segue ne esamineremo in dettaglio una delle ultime evoluzioni, il “FOC” o “Field Oriented Control”.
L’interesse per questa tipologia di controlli nasce principalmente dal vedere “il movimento” di qualcosa, che senza il nostro intervento sarebbe rimasto inanimato, a maggior ragione se l’oggetto in questione viene controllato secondo le nostre esigenze. La storia dei controlli dei motori elettrici è inevitabilmente connessa all’evoluzione che ha caratterizzato gli attuatori elettromeccanici. In passato il motore in corrente continua era quello maggiormente utilizzato nei campi dove era richiesta una velocità variabile o il controllo di coppia. La propensione all’utilizzo di tale azionamento era dovuta alla relativa semplicità nel controllo di velocità, a discapito, tuttavia, di numerosi svantaggi rispetto ai motori in corrente alternata quali, ad esempio, la necessità di manutenzione periodica (su collettore e spazzole), la velocità di rotazione limitata, una bassa resistenza al sovraccarico ed elevate dimensioni. Si è quindi scelto di utilizzare i motori a corrente alternata, i quali risolvono buona parte dei problemi succitati a fronte di un notevole aumento della complessità per il controllo. Essi, infatti, erano inizialmente utilizzati come azionamenti a velocità costante, e solo negli anni ‘80, grazie all’avvento di nuove tecniche nell’elettronica di potenza (come IGBT, MOSFET e BJT), è stato possibile iniziare fattivamente lo sviluppo di sistemi di controllo per tali azionamenti.
LE BASI DELL’AZIONAMENTO
Il principio di funzionamento dei motori asincroni (senza necessariamente scendere troppo nei particolari) si basa sulla generazione di un “campo magnetico rotante”, ovvero il campo magnetico generato da due bobine alimentate dalla stessa tensione alternata ma sfasate tra loro. Tale campo avrà una velocità di rotazione costante, e se all’interno di esso posizioniamo un oggetto metallico cilindrico (sensibile ai campi magnetici), all’interno di questo si genereranno delle correnti elettriche dette “correnti indotte”, le quali creeranno a loro volta un complesso di forze elettromagnetiche che porterà alla rotazione del rotore. Il primo ad utilizzare tale principio fu il Torinese Galileo Ferraris, il quale costruì un rudimentale motore asincrono utilizzando due bobine ed un rotore cilindrico in rame vuoto. Oggi la struttura di un motore asincrono è ben diversa dal prototipo di Ferraris, ma si basa esattamente sullo stesso principio. In Figura 1 è riportato lo spaccato di un motore asincrono. In questo articolo si farà riferimento a sistemi di alimentazione trifase, dato che si sposano benissimo con l’esigenza funzionale di tale macchina elettrica di avere le tensioni di alimentazione sfasate.
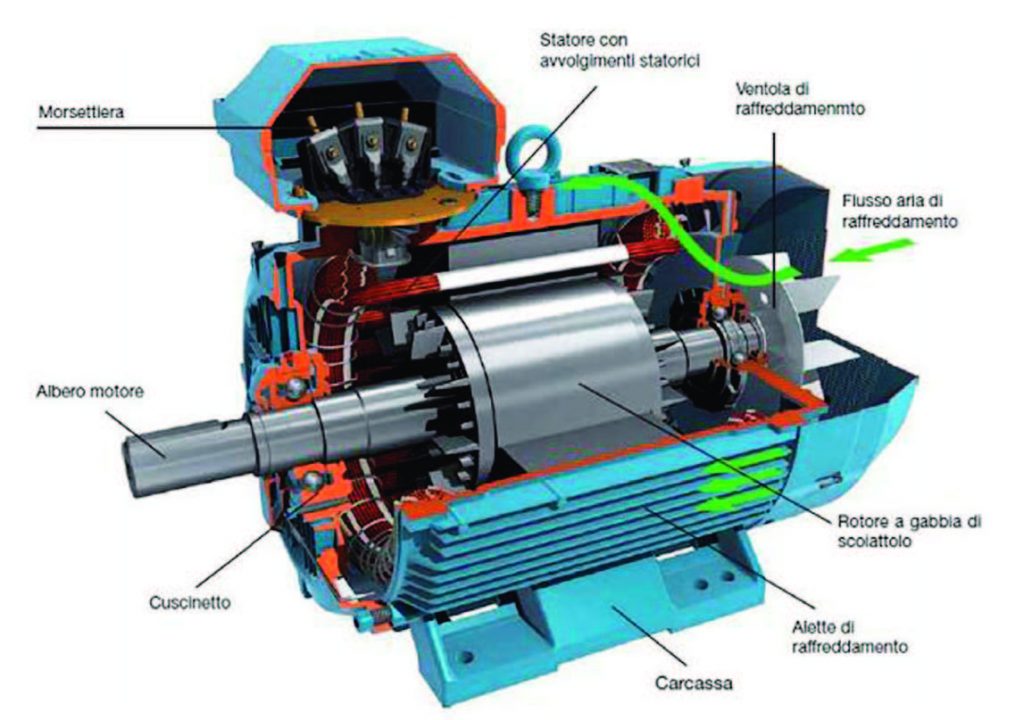
Figura 1: Spaccato di un motore asincrono
Il modo più semplice ed economico per regolare in modo continuo la velocità di un motore asincrono trifase, consiste nel variarne lo scorrimento riducendo la tensione statorica o aumentando la resistenza rotorica. Questo può avvenire poiché gli avvolgimenti rotorici sono connessi, mediante anelli e spazzole, ad un reostato. Questa tipologia di controllo ha l’indubbio vantaggio del basso costo e ridotta manutenzione, oltre ad un buon fattore potenza/coppia, mentre gli svantaggi consistono in uno scarso rendimento, una dinamica bassissima e la necessità di avere il “rotore avvolto”. Un altro tipo di controllo molto usato è il “V/f”, detto anche “controllo scalare”, poiché si fa in modo di mantenere il rapporto Tensione/Frequenza costante, seguendo la regola: Cmax=k(Vs/fs)2, in modo da garantire al motore condizioni di lavoro ideali. La grandezza che controllerà la velocità di rotazione sarà la frequenza di alimentazione. In Figura 2 è riportato l’andamento coppia - velocità al variare del rapporto V/f. A fronte dei vantaggi relativi al basso costo per il controllo, troviamo lo svantaggio della dinamica, ancora ben lontana da quella di un motore in corrente continua. Il motivo per cui i motori asincroni stanno vivendo una seconda giovinezza è l’avvento del controllo FOC (Field Oriented Control), che basa la sua forza sull’utilizzo di un microcontrollore in grado di fornire la potenza matematica necessaria per disaccoppiare la generazione di coppia dalla magnetizzazione, proprio come avviene in un motore DC.
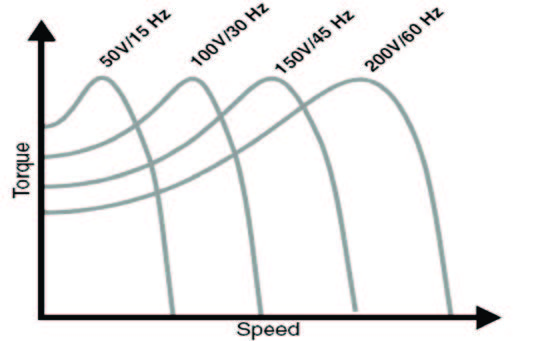
Figura 2: Famiglia di curve con andamenti Coppia - Velocità al variare del rapporto V/f
LA FILOSOFIA DEL FOC
Nei motori DC a spazzole, il flusso allo statore ed al rotore sono mantenuti rispettivamente a 90 gradi, generando così la coppia massima che il motore può erogare. Usando la tecnica FOC le correnti del motore sono trasformate in vettori a due assi, confrontabili con quelli di un motore DC. Per disaccoppiare flusso e coppia è necessario impegnarsi in diverse trasformazioni matematiche, ed è qui che i microcontrollori forniscono il loro valore aggiunto in termini di prestazioni. Infatti, la capacità di elaborazione fornita da questi sistemi permette di effettuare le operazioni matematiche molto rapidamente. Ciò implica che l’intero algoritmo di controllo del motore può essere eseguito ad un ritmo veloce, consentendo così una maggiore dinamica. In un motore trifase, le tre correnti risultano sfasate di 120°, ottenendo una corrente statorica data dalla somma (vettoriale) delle tre componenti, come mostrato in Figura 3.
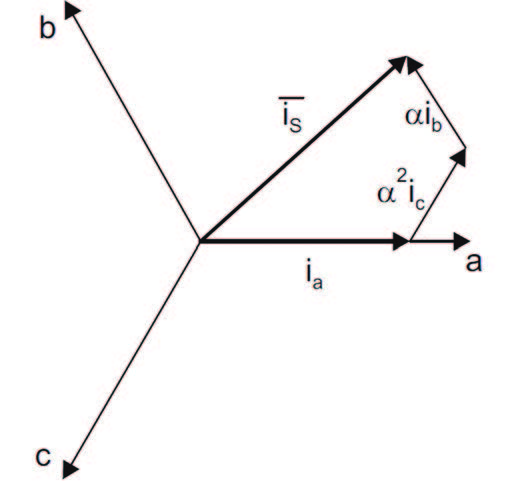
Figura 3: Grafico vettoriale delle tre correnti fase e componente risultante
Le “Trasformazioni” a cui si faceva riferimento prima, servono a rendere la corrente statorica dipendente da soli due parametri “tempo - invarianti”, tramite le seguenti operazioni:
1) Trasformata di Clark Is (a,b,c) → Is (α,β ): Che rende la Is (corrente statorica) funzione di due grandezze tempo varianti invece che tre, come mostrato in Figura 4.
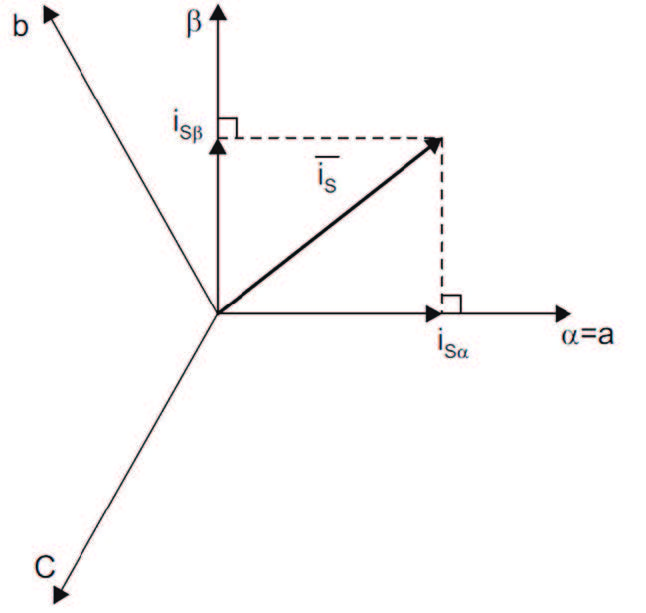
Figura 4: Rappresentazione grafica della trasformata di Clarke
2) Trasformata di Park Is (α,β ) → Is (d,q): che rende la corrente statorica funzione di due grandezze tempo invarianti, come mostrato in Figura 5.
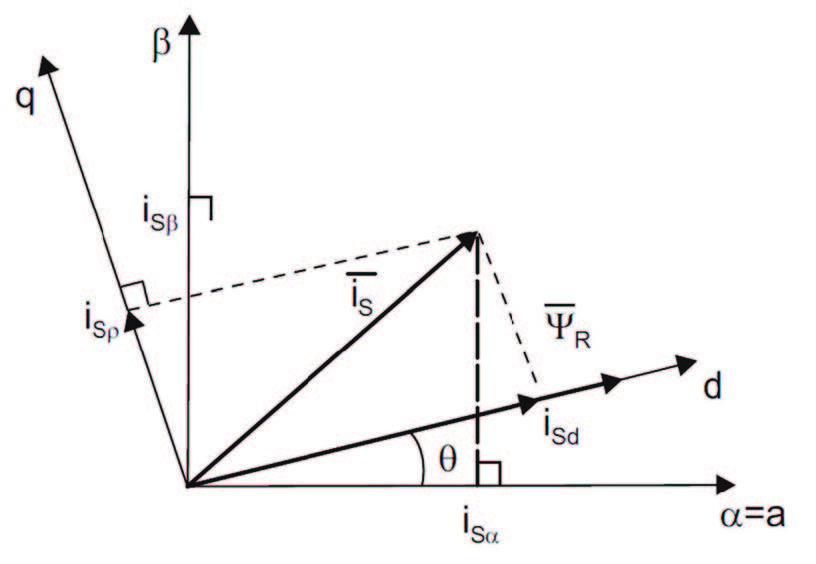
Figura 5: Rappresentazione grafica della trasformata di Park
Da quest’ultima trasformazione si ottiene un sistema di questo tipo:
isd = is cosθ + is sinθ
isq = is cosθ - is sinθ
dove θ è l’angolo di rotazione del flusso rotorico, mentre isd e isq sono, rispettivamente, le componenti della corrente di flusso e coppia (indipendenti tra loro). È semplice intuire come il principale sforzo del controllo sta nell’ottenere l’esatta posizione angolare del flusso rotorico. In Figura 6 è riportato lo schema a blocchi funzionale di un controllore FOC.
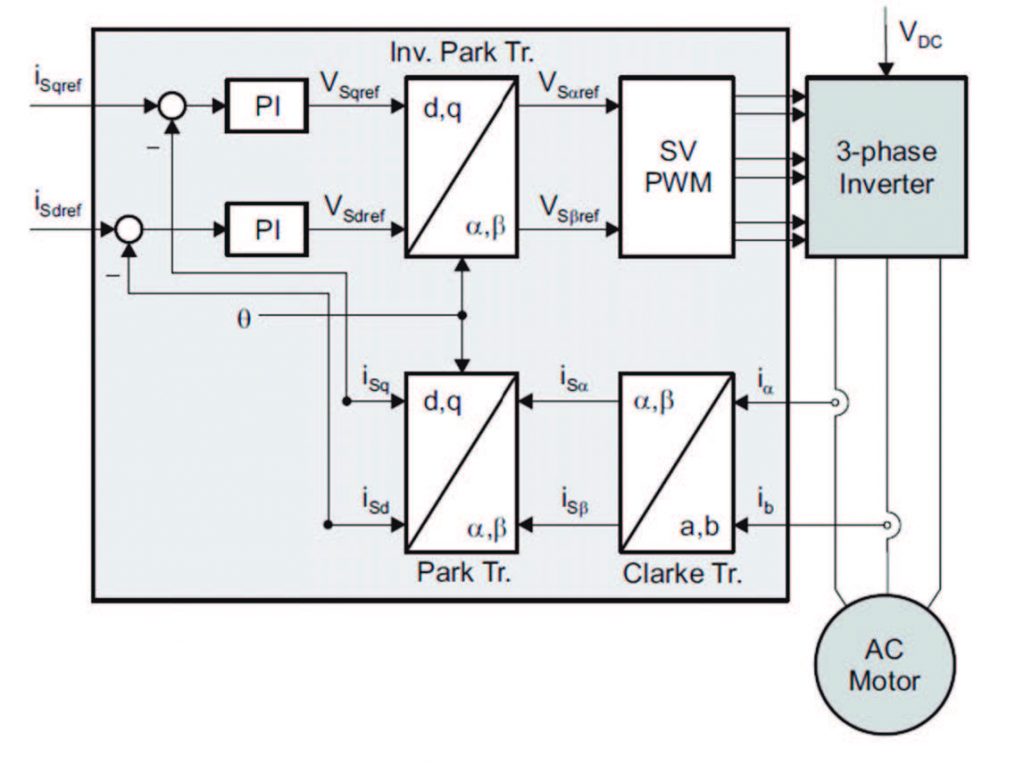
Figura 6: Schema a blocchi funzionale di un controllore FOC
Il processo inizia misurando le correnti del motore trifase: dato che la somma dei tre valori di corrente istantanei sarà nulla, solo due delle tre correnti necessitano di essere misurate e il valore della terza corrente è calcolato a partire dalle misure risultanti. Questo fornisce una riduzione immediata nei costi per l’hardware, perché sono richiesti solo due sensori di corrente. Attraverso le due trasformazioni (prima di Clarke e poi di Park), si ottengono le due componenti di corrente rotorica e di flusso. Confrontando quanto ottenuto con i due riferimenti, si ottiene un segnale di errore che a sua volta va in ingresso ad un controllore PI (controllore Proporzionale Integrale), che lo trasforma in un riferimento di tensione. Dato che il motore dovrà essere controllato fornendo ad un inverter i valori di tensioni delle tre fasi, viene effettuata una trasformazione di Park inversa, che rende i due riferimenti non più funzione di p e q, ma di α e β che, dati in pasto ad un modulatore PWM, consentono il pilotaggio di un inverter trifase. Come accennato prima, il cardine di questo controllo sta nel calcolo dell’angolo θ, il quale, in caso di errata stima, provoca non pochi problemi nella generazione dei riferimenti. I metodi per il calcolo di θ dipendono dal tipo di motore con il quale si lavora. Macchine Sincrone: dato che la velocità del rotore è uguale alla velocità del flusso rotorico, è sufficiente misurare tale posizione con un sensore (ad esempio un encoder). Macchine Asincrone: in questo caso la velocità di rotazione del rotore è diversa dalla velocità del flusso rotorico. Le possibili strade sono due: il metodo di stima indiretto, nel quale è necessario l’ausilio di un modello del motore (funzione di d, q e velocità di rotazione del rotore) per stimare tale angolo, oppure il metodo diretto, che attraverso un sensore ad effetto Hall (sensore di flusso) ricava θ.
IL CONTROLLO VISTO DAL MICRO
L’utilizzo di un microcontrollore per la gestione di questa tipologia di sistemi implica notevoli vantaggi, a partire da:
- riduzione dei costi, dato che si avrà un’unica unità che eseguirà tutto il controllo;
- possibilità di riduzione del ripple di coppia, con conseguente riduzione di rumore e vibrazioni ed aumento del tempo di vita media della macchina elettrica;
- riduzione delle armoniche generate dall’inverter, evitando così il costo di un filtro;
- utilizzo di algoritmi “sensorless”, che permettono di non utilizzare sensori di posizione o velocità;
- generazione di segnale PWM per il controllo dell’inverter.
I fattori appena elencati rappresentano il valore aggiunto più facilmente ottenibile; se ci si vuole spingere più profondamente in quelli che sono i sistemi di controllo e la potenzialità di un microcontrollore a 32 bit, si può ricorrere all’utilizzo di Reti neurali o Logica Fuzzy, oltre ad algoritmi adattativi e sistemi diagnostici basati sulla risposta in frequenza. La Texas Instruments, attraverso l’ausilio di un microcontrollore della famiglia C2000 (il TMS320F2803x), ci permette di eseguire egregiamente quanto appena detto. La serie TMS320F2803x fa parte della famiglia dei microcontrollori “Piccolo”, sistemi di nuova generazione prodotti dalla casa americana. La Texas ha realizzato due grandi categorie per la prossima generazione di microcontrollori. La serie “Delfino” caratterizzata da micro con package di dimensioni più spinte (fino a 256 pin) e indici di prestazione di tutto rispetto (nell’ordine dei 600 MFLOPS). La serie “Piccolo”, a cui appartiene il micro F2803x descritto in questo articolo, possiede caratteristiche che non lasciano certo indifferenti (da 64 a 128 KB di Flash 16 Ch e ADC a 12 bit), come mostrato in Figura 7.
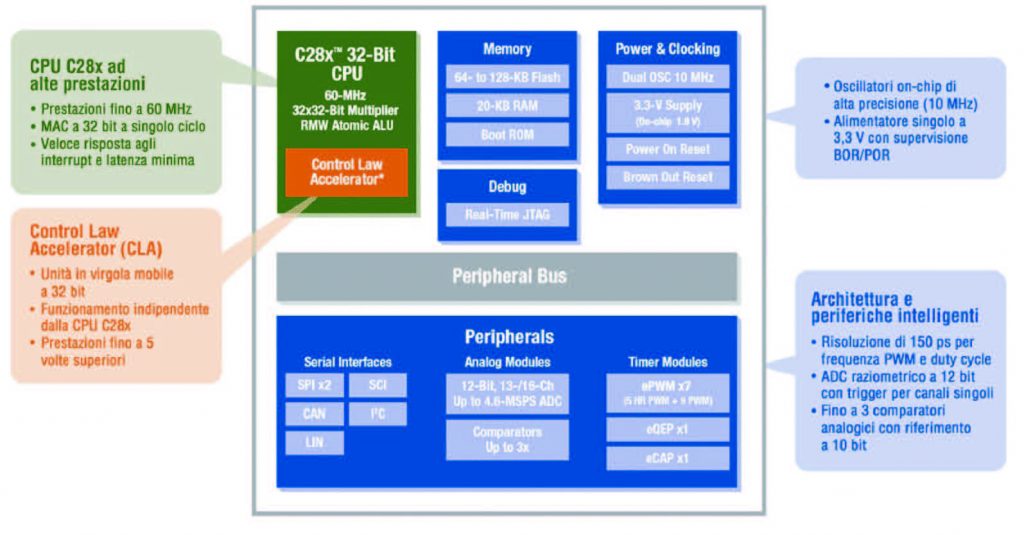
Figura 7: Caratteristiche del micro serie Piccolo
STRUTTURA DEL CONTROLLO SOFTWARE
In questo articolo si farà riferimento ad un controllo di tipo indiretto, ovvero si stimerà il valore della posizione angolare del flusso rotorico, calcolandolo in base alla velocità del rotore. In Figura 8 è mostrato lo schema a blocchi di un controllo di tipo indiretto.
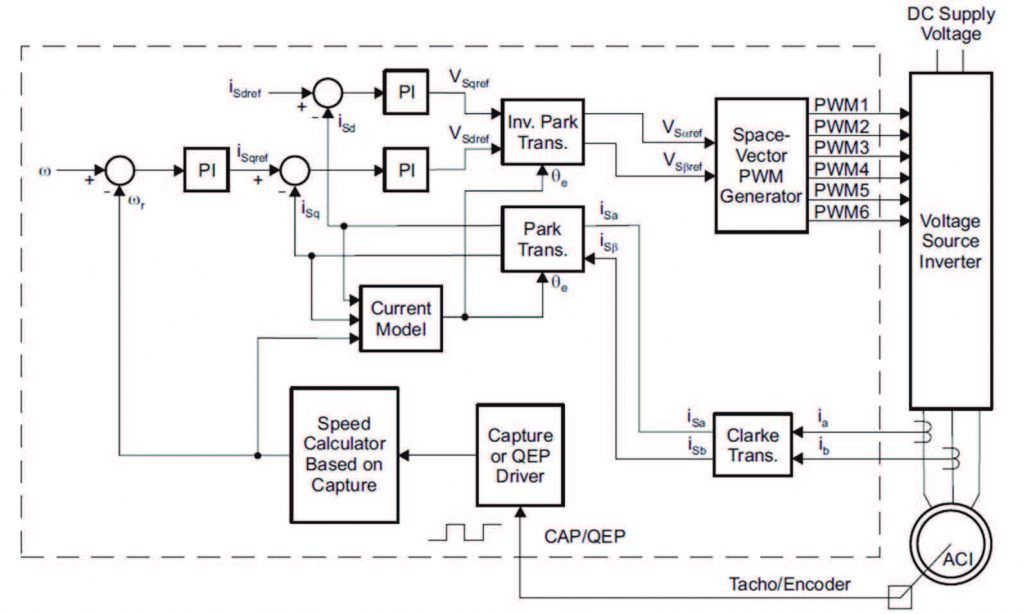
Figura 8: Schema a blocchi del controllo FOC di tipo indiretto
Lo schema mostra come la parte inferiore, attraverso un modello, stimi la posizione dell’angolo θ. Si può immaginare che ogni blocco dello schema raffigurato venga trattato come una Macro, quindi come un modulo che riceve degli input in ingresso e trasforma tali segnali in uscite utili al controllo. La Tabella 1 mostra il nome di ogni modulo e quali operazioni al suo interno vengono effettuate.

Tabella 1: Nome dei moduli SW e descrizione
Il primo step del controllo è mostrato in Figura 9, si basa sulla lettura della velocità attraverso un sensore di tipo QEP, che dopo essere stato acquisito dal driver, viene elaborato dalla rispettiva Macro QEP, ottenendo la posizione θ del rotore e la direzione di rotazione.
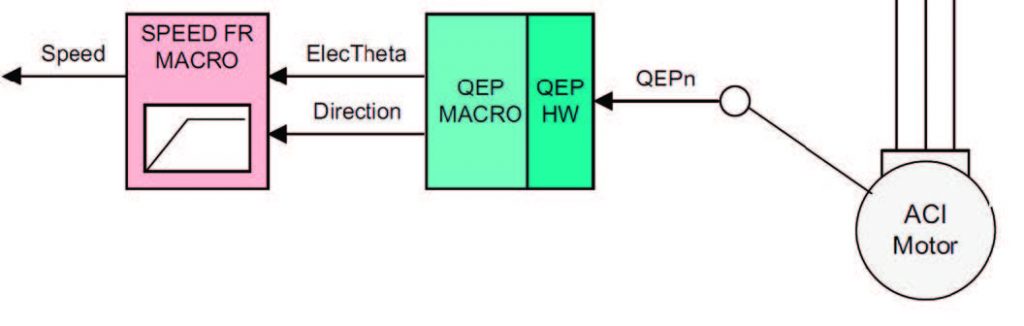
Figura 9: Lettura della posizione del rotore ed elaborazione per ottenere velocità e direzione di rotazione
Il segnale verrà poi elaborato dalla macro SPEED_FR, che ne calcolerà la velocità, e la grandezza così ottenuta verrà confrontata con il riferimento per il controllo di velocità, e inviata al modello per la generazione del θ stimato. In Figura 10 si può osservare come dal motore vengono in contemporanea lette le tre correnti, e attraverso un convertitore ADC, vengono date in pasto prima alla trasformata di Clarke e poi a quella di Park, ottenendo così le due componenti tempo invarianti di flusso (Ds) e coppia (Qs), utilizzate come feedback per il controllo.

Figura 10: Lettura delle correnti trifase e trasformazioni di Clarke e Park per ottenere i due riferimenti tempo - invarianti
È semplice verificare come in ingresso il sistema prenda un riferimento di velocità ed un riferimento di corrente (proporzionale alla coppia, come nei motori DC) mostrato in Figura 11.
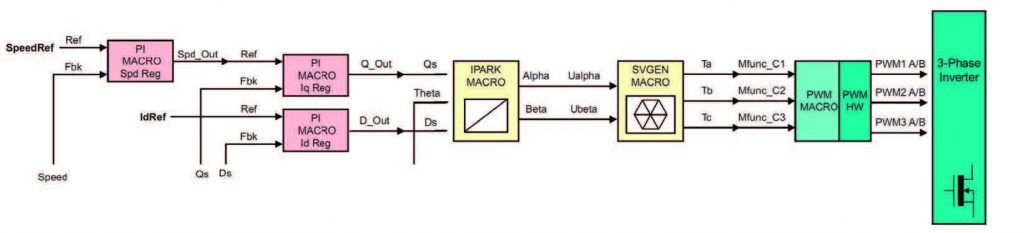
Figura 11: Lettura dei riferimenti e flusso di controllo della catena diretta
Il primo regolatore PI genera la corrente di riferimento Iq che viene confrontata con la Qs, ricavata dalla trasformata di Park in Figura 10, mentre il riferimento IdRef viene confrontato con la Ds nel controller PI. Le uscite dei due controllori forniscono in uscita rispettivamente la Q_out e la D_out, ovvero le due componenti di coppia e flusso che andranno a pilotare l’inverter trifase. Prima, però, è necessario applicare la trasformata inversa di Park per riportare le due componenti in funzione del tempo (α, β). Al fine di generare la terna per il controllo PWM, si utilizza un controller in quadratura (SVGEN, Space Vector Generation), che genererà i tre segnali PWM con andamento sinusoidale come mostrato in Figura 12.
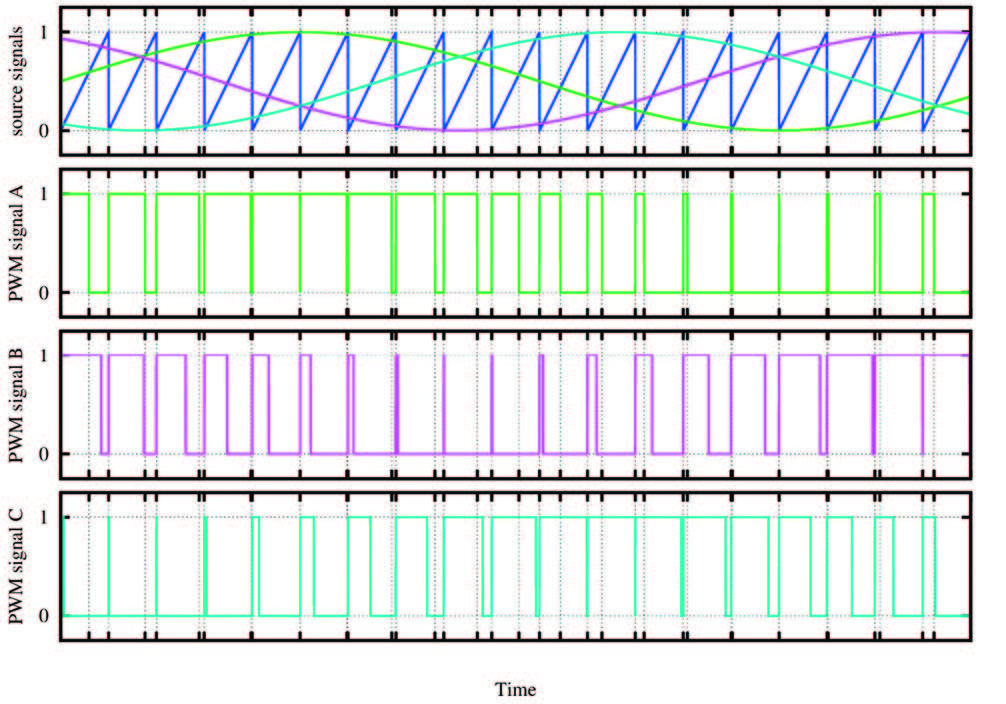
Figura 12: Segnali trifase dopo l’elaborazione per la generazione del segnale PWM
Infine, i tre segnali dati in ingresso ad un controller PWM, gestiscono la parte relativa alla potenza attraverso 6 ponti ad H (due per ogni fase), come mostrato in Figura 13.
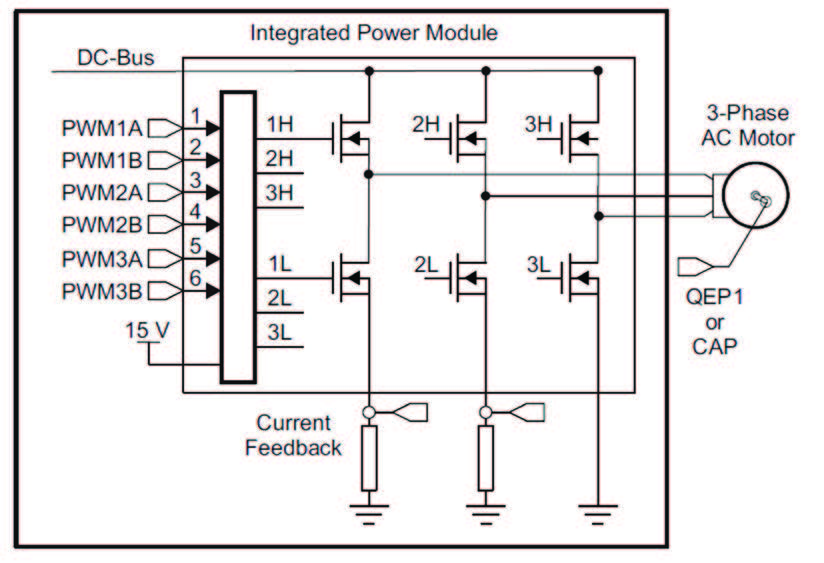
Figura 13: Schema controllo del sistema di potenza
Infine, in Figura 14 è riepilogato lo schema dell’intero sistema, composto da tutti gli insiemi di blocchi funzionali precedentemente analizzati. Dall’immagine si può osservare come, partendo da un riferimento di velocità e corrente (SpeedRef e IdRef), si effettua il confronto con i due segnali di feedback ricavati dal sistema meccanico attraverso la doppia “catena inversa”. La prima sequenza di blocchi ricava il feedback di corrente, infatti leggendo le tre correnti di fase che alimentano il motore (attraverso ADC MACRO), verrà eseguita la conversione delle grandezze funzioni del tempo in misure tempo invarianti (con le due Macro di CLARKE e PARK), direttamente correlate con coppia e flusso. La seconda sequenza rileva attraverso un sensore la posizione del rotore (QEP MACRO), e ne calcola la velocità di rotazione (SPEED FR MACRO). Tale grandezza viene poi data in pasto al regolatore di velocità (PI MACRO Spd Reg). Come già anticipato, la tecnica FOC presenta come unico limite il rapido calcolo dell’angolo θ, ed i microcontrollori sopperiscono al problema in maniera eccellente, permettendo di ricavare istante per istante questa grandezza. Attraverso il modello della macchina elettrica implementato sull’unita di elaborazione (CURMOD MACRO) si ottiene l’angolo θ, il quale è dato in ingresso ai due moduli che effettuano la trasformata e l’anti trasformata di Park. Nello specifico, la trasformata inversa di Park (IPARK MACRO) riceve in ingresso i segnali errori processati dai regolatori della Iq (PI MACRO Iq Reg) ed Id (PI MACRO Id Reg) che, a sua volta, genera due riferimenti tempo varianti (α, β). Attraverso un controller in quadratura (SVGEN MACRO) verranno generati i tre segnali di comando, opportunamente convertiti attraverso il controller PWM (PWM MACRO) al fine di ottimizzare la gestione dell’inverter trifase.
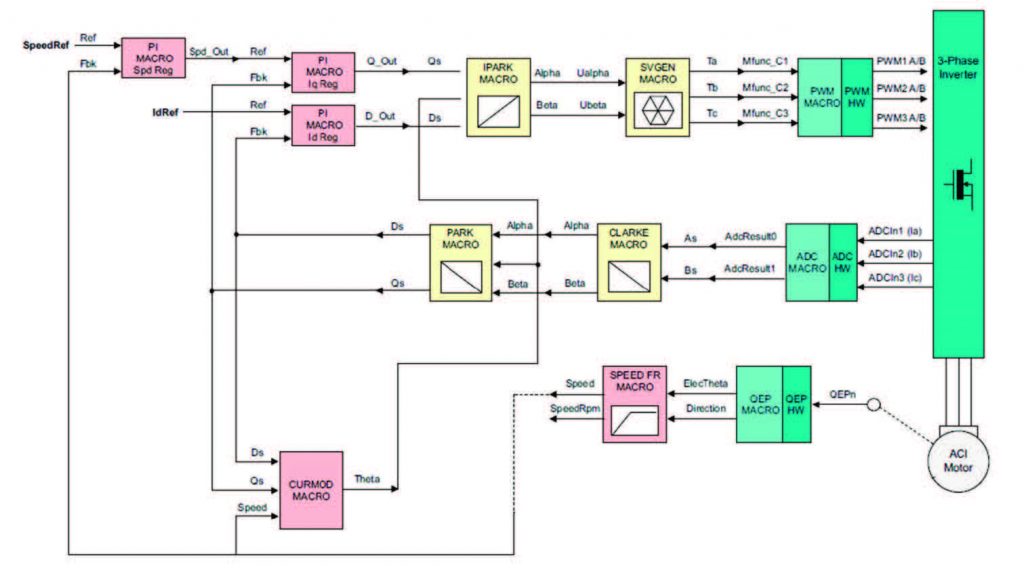
Figura 14: Schema completo del sistema di controllo FOC
CONCLUSIONI
Se fino a qualche anno fa l’idea di fornire ad un motore AC la stessa dinamica di uno in corrente continua era solo un’astrazione matematica, attuabile solo attraverso modelli numerici e simulazioni al computer, oggi le nuove generazioni di microcontrollori, aventi prestazioni paragonabili a quelle di mini computer, permettono di integrare l’intero sistema di controllo in una singola scheda dedicata. Il vantaggio di questa tipologia di controllo si può facilmente riscontrare in quella che è la vita quotidiana, in quanto non solo favorisce le applicazioni di tipo industriale, ma soprattutto le applicazioni di tipo domestico, (si pensi alle lavatrici, dove viene migliorata l’efficienza energetica e ridotto il rumore udibile).




