In questo articolo è presentato il modello e l'algoritmo di controllo sviluppato per la guida di un robot mobile capace di seguire una parete (wall follower), principio utilizzato poi per realizzare un robot pattugliatore. Arduino, in particolare la versione Mega 2560, è stato scelto come unità di controllo. L'algoritmo, attraverso una coppia di sensori ad ultrasuoni HC-SR04, scandaglia l'ambiente acquisendo misure di distanza, regolando così la sua traiettoria seguendo la linea della parete. Il robot è anche in grado di rilevare la presenza di eventuali ostacoli, grazie ad un sensore frontale (sempre ad ultrasuoni), così da variare il percorso per evitare eventuali collisioni. Il sistema di controllo è progettato per garantire l'asintotica stabilità del sistema evitando la saturazione degli attuatori, e quindi un loro irrimediabile danneggiamento. Saranno illustrati e descritti tutti i passaggi, come del resto anche le componenti utilizzate ed i relativi schemi circuitali, seguiti per la messa in pratica dell'idea. Infine, saranno forniti link a video che mostrano i risultati sperimentali e quindi la validità dell'approccio seguito.
Introduzione
Al giorno d'oggi, le applicazioni che coinvolgono agenti autonomi stanno aumentando ad un ritmo elevato e si prevede che tale tendenza continui anche nel futuro grazie a progressi tecnologici che apriranno la strada a nuove possibilità applicative. Tali dispositivi trovano impiego non solo ai fini della ricerca ma anche in contesti quotidiani. Ad esempio, si pensi a robot per la ricerca ed il recupero di dispersi in seguito ad eventi tragici oppure a robot in grado di pulire automaticamente i pavimenti delle abitazioni, o ancora quelli in grado di tagliare (impostata una lunghezza desiderata) l'erba del giardino.

Figura 1: Screen della missione di un robot, tratto da un ambiente di realtà virtuale, nel mentre si accinge all'esplorazione di Marte
Il problema del patrolling o della circumnavigazione di un oggetto consiste nel guidare un agente (un generico robot) lungo il bordo di un ostacolo garantendo il mantenimento di una distanza minima da esso. Al di là del semplice pattugliamento, il patrolling trova applicazione nel più generale problema della navigazione di un ambiente sconosciuto (in letteratura noto come SLAM, che sta per Simultaneous Localization and Mapping), in cui si vuole che un agente sia in grado di raggiungere un punto nello spazio, detto goal (obiettivo), utilizzando solo informazioni locali ottenute attraverso sensori atti alla rilevazione di oggetti. Infatti, la soluzione più intuitiva a questo problema vuole che l'agente si diriga verso il goal fino all'individuazione di un ostacolo, per poi procedere al patrolling fino a quando il percorso per l'obiettivo torna ad essere libero da impedimenti. In Figura 1 è riportato uno screen della missione spaziale Curiosity della NASA, tra gli obiettivi l'esplorazione di Marte, tipico esempio di un robot pattugliatore.
Le applicazioni spaziali non sono le uniche in cui i robot pattugliatori trovano impiego. In Figura 2 è riportato un esempio di soluzione aziendale utilizzata per monitorare i perimetri di impianti industriali, dotata di camera omnidirezionale e pan-tilt-zoom.

Figura 2: Robot autonomo impiegato per il monitoraggio di impianti industriali
L'obiettivo del lavoro è illustrare i passi che hanno permesso la realizzazione di un robot pattugliatore utilizzando Arduino Mega 2560, una serie di sensori ad ultrasuoni (gli HC-SR04, già introdotti all'interno di un precedente articolo) per l'analisi dell'ambiente e l'individuazione di eventuali ostacoli, mentre la movimentazione è affidata a due coppie di motori DC (Direct Current, Corrente Continua) che consentono al robot di spostarsi nell'ambiente lavorando in modalità skid steering (abbiamo già discusso di questa modalità).
Modello cinematico
Consideriamo il modello dell'uniciclo - approssimazione valida dato che il robot scelto lavora in modalità skid steering - posizionato ad una distanza diversa da zero rispetto all'obiettivo (xd in Figura 3) in un sistema di riferimento cartesiano. Il suo moto lungo l'obiettivo è governato dall'azione combinata della velocità angolare ω e della velocità lineare u, la quale è sempre nella direzione di uno dei due assi del frame <a> attaccato al robot.
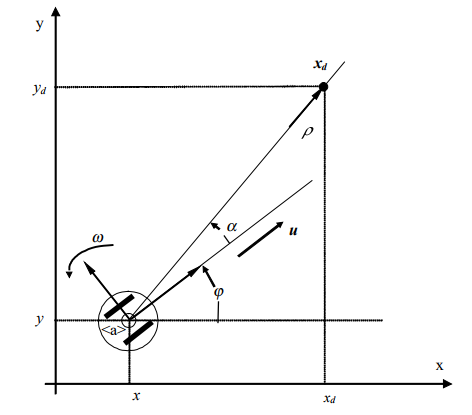
Figura 3: Posizione ed orientamento del robot nello spazio
Dunque, l'usuale insieme di equazioni che governano la dinamica del robot, nel sistema cartesiano [x, y] dato l'angolo di imbardata φ, è:
![]()
dove φ è misurato rispetto all'asse x.
Consideriamo ora il caso di un robot intento nel navigare un corridoio (Figura 4). Le variabili di stato cambiano rispetto al caso precedente, e sono definite in relazione al corridoio come x̃ tilde e φ, dove x̃ rappresenta la deviazione del robot dal centro del corridoio (o la linea che si desidera seguire) e φ è la deviazione angolare rispetto all'asse del corridoio. In questo caso le equazioni cinematiche si riducono a:
![]()
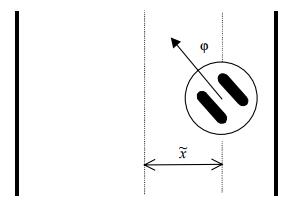
Figura 4: Robot intento a navigare un corridoio
Capite le equazioni generali (eq. 1) e particolari (eq. 2) che governano la dinamica del sistema, è possibile formulare l'algoritmo di controllo che varia le velocità degli attuatori seguire la linea della parete.
Il sistema di controllo
Per la realizzazione del sistema di controllo si è preso in considerazione il sistema rappresentato in Figura 5. Rispetto al caso precedente, le variabili di stato sono definite in relazione alla parete come φ e ᵭ, dove φ è la deviazione angolare relativa alla linea delle mura, mentre ᵭ rappresenta la distanza del robot da una linea immaginaria ad una desiderata distanza dwall.
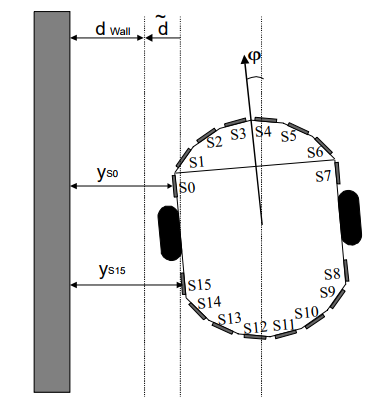
Figura 5: Schema del robot nel mentre insegue la parete
In Figura 5 sono rappresentati anche i sensori ad ultrasuoni, indicati con si (dove con i è indicato il sensore i-esimo), in grado di misurare la distanza ys0 e ys15. In questo caso la distanza ᵭ è calcolata come:
![]()
dove il segno più o meno è da tenersi a mente nel caso in cui il robot segua la parete dal lato destro (nel nostro caso la stiamo seguendo dal lato sinistro). Il robot è anche capace di rilevare la presenza di eventuali ostacoli, deviandoli. Per questo è dotato di un sensore aggiuntivo, posto sulla parte frontale, che conferisce la capacità, come suddetto, di evitare gli ostacoli che potrebbero eventualmente presentarsi davanti al robot intento a seguire la parete. A questo scopo, si considera un segnale di deviazione come una perturbazione ωp verso il sistema di controllo, come mostrato in Figura 6.
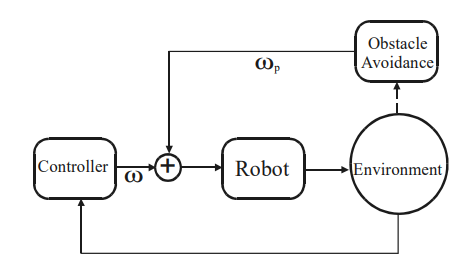
Figura 6: Schema sistema di controllo con rilevatore di ostacoli
Il segnale è calcolato sulla base della posizione ᵭ fornita dal sistema di controllo, descritta in precedenza. L'algoritmo di controllo è in grado, così, di guidare il robot dal punto iniziale a quello finale, l'obiettivo xd visto in Figura 3. Così come è strutturato, il rilevatore non influisce sulla guida del veicolo nel mentre è intento a seguire una parete. Quando viene rilevato un ostacolo, il sistema di controllo genera un segnale di comando ωp in grado di evitare la collisione puntando ad un nuovo obiettivo xr, così come descritto dall'equazione seguente:
![]()
e visibile in Figura 7, dove ψ rappresenta l'angolo di rotazione con cui il robot evita l'ostacolo. [...]
ATTENZIONE: quello che hai appena letto è solo un estratto, l'Articolo Tecnico completo è composto da ben 2392 parole ed è riservato agli ABBONATI. Con l'Abbonamento avrai anche accesso a tutti gli altri Articoli Tecnici che potrai leggere in formato PDF per un anno. ABBONATI ORA, è semplice e sicuro.