I microcontrollori general-purpose spesso non dispongono di un coprocessore matematico integrato per svolgere i più comuni algoritmi di calcolo in virgola fissa o mobile come avviene invece in dispositivi specializzati come i Digital Signal Processors o nelle Cpu dei moderni Pc. Per questo motivo nasce l’esigenza di creare routines adatte alla particolare architettura hardware che si sta utilizzando; tali algoritmi devono essere ottimizzati al fine di rendere minimo il tempo di calcolo e dunque vanno realizzati in Assembler, ricorrendo ad istruzioni specifiche dei micro destinati alla loro esecuzione. Oltre ad essere interessanti di per sé, questi argomenti sono di importanza fondamentale poiché toccano alcuni aspetti fondamentali di un sistema di elaborazione, inteso nel senso più specifico come macchina per svolgere calcoli.
Somma e sottrazione
L’operazione di somma con i numeri interi positivi va effettuata in binario con la stessa modalità con cui viene effettuata in decimale. Partendo dalla colonna più a destra si calcola, per ogni colonna, la somma delle cifre corrispondenti degli addendi, più un eventuale riporto generato dalla colonna precedente. Per realizzare questo algoritmo bisogna conoscere il valore della cifra di somma e quella di riporto che vengono generate da tutte le possibili combinazioni delle cifre nella base scelta. Per la base 2, per esempio si hanno i seguenti casi possibili:
0 +0 +0 = 0 con riporto di 0
1+0+0 = 0+1+0 = 0+0+1 = 1 con riporto di 0
1+1+0 = 1+0+1 = 0+1+1 =0 con riporto di 1
Per esempio utilizzando quattro bit si considerino i casi seguenti delle somme
3+7 e 9+7

Nell’esempio di destra si può notare come la somma produca un riporto generato nella colonna dei bit più significativi, che deborda a sinistra dalla rappresentazione tramite nibble. Questo riporto in uscita a sinistra indica che si è prodotto un overflow, ovvero il risultato è talmente grande che non può più essere rappresentato con il numero di bit prescelto: il massimo numero consentito sarebbe infatti 15 e il risultato errato è indicato chiaramente dalla presenza dei 4 zeri all’interno delle posizioni utili. Situazioni di questo genere vanno tenute in considerazione durante la stesura delle routine. Per poter essere sicuri di non incorrere in situazioni di overflow, bisogna garantire che la rappresentazione della somma abbia almeno 1 bit in più rispetto a quella dell’operando più lungo. In generale se sommo K numeri di N bit, la minima lunghezza della rappresentazione del risultato che garantisca dall’overflow è N + log(2) K. Per quanto riguarda la sottrazione le regole cambiano leggermente: si procede sempre da destra verso sinistra, a ogni colonna va sottratto al bit del primo operando quello del secondo e anche un eventuale prestito usato nella colonna precedente.
0 - 0 - 0 = 1 - 1 - 0 = 1 -0 -1 = 0 con prestito di 0
0 - 1 - 0 = 0 - 0 – 1 = 1 -1 -1 = 1 con prestito di 1
1 - 0 - 0 = 1 con prestito di 0
0 - 1 - 1 = 0 con prestito di 1
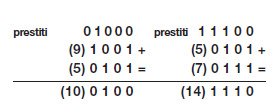
Anche in questo caso l’esempio di destra mostra un errore dovuto ad un prestito uscente dalla colonna più a sinistra. Il risultato sarebbe negativo ma la rappresentazione utilizzata considera solamente numeri positivi in rappresentazione binaria diretta. Per i numeri negativi vediamo qualche esempio in complemento a due, utilizzando come formato il byte. Come già ricordato, con questa rappresentazione non è necessario trattare il caso della sottrazione poiché essa si riduce alla somma del complemento.

L’esempio 1 mostra un’operazione corretta, mentre l’esempio 2 dà un risultato sbagliato poiché si è verificato un overflow dato da un uno entrante nella posizione destinata al bit di segno e nessun carry uscente. Si vedano gli altri due esempi.

Questa volta l’esempio 2 mostra un risultato corretto anche se c’è un riporto entrante nel bit di segno, perché contemporaneamente vi è un riporto uscente (carry). L’esempio 1 presenta invece un risultato errato poiché si ha un riporto uscente (carry) ma non un bit di riporto entrante nel bit di segno: in questo caso si verifica un underflow: due numeri negativi sommati danno un risultato positivo. Dagli esempi visti si possono trarre alcune considerazioni riguardo ai possibili overflow nelle somme (sottrazioni) in complemento a due. Per due numeri di segno diverso non è possibile overflow; per due numeri positivi, l’overflow è rilevato da un carry nel bit di segno; per due numeri negativi, l’overflow è rilevato da nessun carr y nel bit di segno ma da un carr y fuori dal bit di segno. In generale non ci sarà overflow e quindi errori nel caso si abbia contemporaneamente un bit entrante e uno uscente dal bit di segno. Se si sa che il risultato di una certa operazione rientra nel range della rappresentazione, allora non ci può essere overflow, altrimenti sarà necessario controllare direttamente i carry in corrispondenza del bit di segno.
Moltiplicazione
Anche nel caso della moltiplicazione gli algoritmi adottati ricalcano le operazioni che si svolgono con i calcoli manuali. Iniziamo a considerare i numeri senza segno. Il meccanismo della moltiplicazione consiste nel partire dalla cifra meno significativa del moltiplicatore, moltiplicare tutto il moltiplicando per quella cifra e ottenere un primo risultato parziale; si passa poi a moltiplicare tutto il moltiplicando per la successiva cifra del moltiplicatore e il risultato viene sommato a quello parziale spostandolo di una posizione a sinistra. Si continua in questo modo sino ad esaurire tutte le cifre del moltiplicatore e sommando tutti i risultati parziali. Gli algoritmi potranno essere più o meno ottimizzati in base ai registri della Cpu utilizzata, ma si baseranno sul meccanismo appena visto. Anche nel caso della moltiplicazione si può avere overflow: quest’ultimo si può evitare utilizzando, per salvare il risultato, un registro di lunghezza pari almeno alla somma (m+n) delle cifre binarie di moltiplicatore (m) e moltiplicando (n). Questo vale per interi senza segno. Nel caso di due numeri in rappresentazione modulo e segno, il segno del risultato si ottiene semplicemente tramite un EXOR dei due bit di segno dei fattori e l’overflow si evita salvando il risultato in un registro di lunghezza pari alla somma delle cifre dei due operandi meno uno (m+n-1). Nel caso della rappresentazione in complemento a due, la moltiplicazione può avvenire come quella per i numeri senza segno, tenedo conto del fatto che il bit più significativo del moltiplicatore (il più a sinistra) ha un peso negativo, per cui, se questo bit vale 1, bisogna sottrarre il moltiplicando (o sommare il suo complemento a due) anziché sommarlo. Ci si potrebbe aspettare che, come per i numeri in modulo e segno bastino m+n-1 cifre per salvare il risultato e non incorrere in overflow; in realtà vi è un‘unica combinazione dei due fattori che richiede appunto m+n bit, ed è quella in cui entrambi sono composti di tutti 1 e valgono perciò -2(n-1) e -2(m-1): il prodotto +2(m+n-2) richiede m+n bit per essere rappresentato. Vediamo un esempio di moltiplicazione in complemento a due in cui si esegue il prodotto (-6) per (-3) con fattori su 4 bit e risultato dunque su 8 bit.

Si noti come nei risultati parziali si è effettuato un allungamento della rappresentazione ripetendo a sinistra dei risultati il bit di segno tante volte in modo da ottenere il formato a 8 bit.
Divisione
Ci si limiterà qui a considerare il caso della divisione intera, dal momento che l’algoritmo per il caso generale di divisione con un risultato che presenta un numero illimitato di cifre differisce solo perché ad un certo punto si interrompe il calcolo dei bit del quoziente. Nella divisione intera, il dividendo A, il divisore B, il quoziente Q e il resto R, tutte quantità intere, sono legate dalla relazione A = B*Q + R dove 0 < mod(R)< mod(B) (con mod si intende il modulo) con l’ulteriore vincolo che il resto R abbia lo stesso segno del dividendo. La meccanizzazione della divisione binaria può anche in questo caso ricalcare quello della divisione manuale in base dieci, adattandolo alla base due. In questo caso siamo in presenza di un algoritmo di tipo restoring, dal momento che bisogna ripristinare il valore del resto parziale nel caso una delle sottrazioni intermedie dia risultato negativo. Per migliorare la velocità di esecuzione si utilizzano algoritmi di tipo non-restoring, i quali permettono ad una sottrazione intermedia di dare un risultato negativo: in tal modo non si disfa mai un risultato parziale tornando indietro di un passo, ma, al passo successivo, bisognerà tener conto del risultato negativo ottenuto. Viene di seguito riportato l’algoritmo di divisione in cui si suppone che il dividendo A sia rappresentato da 2n bit, il divisore (B) anche ma occupi solo gli n bit meno significativi e così anche per quoziente e resto. I risultati assunti dai resti parziali sono indicati con Wi, mentre i qi rappresentano i valori successivi del quoziente. Si noti come il divisore (B) viene traslato di n posizioni a sinistra (con la moltiplicazione B*2n, in modo da “allinearsi sotto le cifre del dividendo”: a questo punto inizia l’algoritmo con le sottrazioni successive e il salvataggio dei qi come 0 in caso di risultato della sottrazione negativo e 1 in caso di risultato positivo. Si noti il diverso modo di trattare questi risultati parziali a seconda del segno che hanno, in modo da non dover rieffettuare una nuova sottrazione in caso di risultato negativo. I risultati parziali sono di volta in volta scalati a sinistra tramite una moltiplicazione per 2, anziché far scalare a destra di una posizione la quantità da sottrarre come avviene manualmente:
L’ultimo “if” aggiusta il resto (Wn) in caso di segno negativo. Nella prossima sezione vedremo alcuni di questi algoritmi tradotti in Assembler e specializzati secondo le istruzioni specifiche per i microprocessori della serie Holtek.

Algoritmi di calcolo in Assembler
Le seguenti istruzioni sommano i due numeri data0 (8 bit) e data4 (8 bit), entrambi senza segno, salvando i risultati nei due registri to1-to0 (16 bit). In questo esempio e anche nei successivi “a” rappresenta un generico registro accumulatore. L’ultima istruzione aggiunge semplicemente il valore del carry nella posizione meno significativa di to1.
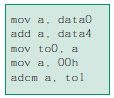
Le seguenti istruzioni sommano due numeri con segno, data0 e data4, salvando il risultato in to1-to0.
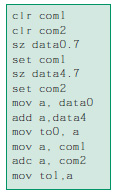
Si noti come in tutte le possibili combinazioni dei segni dei due addendi il segno del risultato viene riprodotto correttamente nel primo bit (il meno significativo) del registro to1. Vediamo il perché: se data0 e data4 sono entrambi positivi (il loro bit 7 è = 0) allora com1 e com2 valgono 0, dunque to1 è anche 0 e il segno è corretto (positivo). Se i due addendi sono negativi (bit 7 = 1), allora com1 e com 2 hanno i bit tutti uguali a 1, la loro somma produce nel primo bit di to1 0; a questo viene però sommato il carry dell’addizione precedente di data0 e data4, e questo sarà sicuramente uguale a 1: ancora una volta il risultato è corretto (negativo). Se i due addendi hanno segni opposti, allora la somma di com1 e com2 produrrebbe un 1 nel primo bit di to1; come prima a questo va aggiunto il carry dell’addizione precedente, il quale è 0 se l’addendo negativo è in modulo maggiore di quello positivo e invece 1 in caso contrario: in entrambi i casi il primo bit di to1 conterrà ancora una volta il segno corretto dell’operazione. Vediamo un esempio di sottrazione di due numeri binari senza segno in formato a 8 bit.
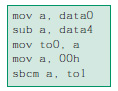
Anche in questo caso il primo bit di to1 contiene il segno del risultato; infatti con l’istruzione “sub” il carry viene settato a 1 se la sottrazione produce un risultato positivo, a 0 altrimenti. Con l’istruzione “sbcm” a 00…00 viene sottratto 00….00 e il complemento del carry (cioè il suo valore negato): in tal modo il primo bit di to1 varrà 0 in caso di risultato positivo e 1 se negativo. Il caso della sottrazione di numeri con segno si può ridurre ad un’addizione sommando il complemento a due del sottraendo e non verrà trattata. Vediamo invece un esempio di moltiplicazione senza segno: l’algoritmo presentato ricalca quello visto in precedenza nell’articolo. Ancora una volta il risultato, a 16 bit, viene salvato in to1-to0.
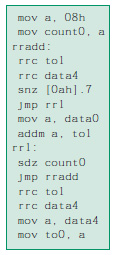
Si noti come nella routine “rradd” viene testato ciascun bit del moltiplicatore (data4):
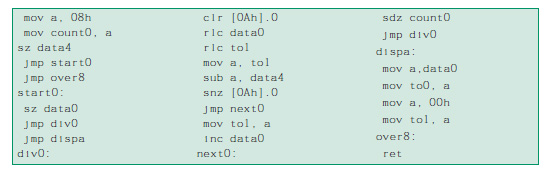
nel caso questo sia 1 si esegue una somma parziale, altrimenti si passa al bit successivo fino ad esaurire tutti i bit (quando count0 = 0). L’algoritmo è ottimizzato dalle due istruzioni consecutive “ rrc to1” “ rrc data4”: esse fanno si che il bit più basso di ogni somma parziale venga di volta in volta caricato nel bit più alto di data4 (si noti che non si ha la perdita del valore precedente di tale bit perché data4 è gia stata traslata a destra e quindi il bit più alto si è già “liberato”); alla fine, così, si ha che data4 contiene il byte più basso del risultato finale, poi trasferito in to0 con i due “mov” consecutivi della routine “rr1” mentre to1 contiene il più alto. Per quanto riguarda la moltiplicazione di numeri con segno in complemento a due si può procedere in questo modo: si fa il complemento a due dei fattori negativi, si esegue una moltiplicazione secondo la routine appena vista valida per numeri senza segno e in questo modo si trova il modulo del risultato; se il segno del prodotto è negativo allora si rifà il complemento a due del modulo appena trovato, altrimenti questo rappresenta già il risultato corretto. Vediamo ancora la divisione senza segno “data0/data4” a produrre to0 (data0). Si noti come il dividendo venga fatto scorrere attraverso il registro to1, partendo dalla cifra più significativa e traslandolo ad ogni ciclo verso sinistra di una posizione: ad ogni passo gli viene sottratto il divisore “data4”; se il risultato della sottrazione è positivo, allora viene prodotto un 1 attraverso il registro “data0”, altrimenti il medesimo percorso viene riservato al bit 0. L’istruzione che discrimina i due casi è quella di controllo del carry “snz [0Ah].0”. In questo modo vengono prodotte in otto cicli tutte le cifre del quoziente, che andranno ad accumularsi in “data0”. In caso di sottrazione con risultato negativo non è necessario ripristinare il valore del sottraendo poiché questo rimane inalterato, dal momento che il risultato (negativo) viene salvato nel registro accumulatore “a” di appoggio tramite l’istruzione “sub a; data4”. Tutti gli esempi visti trattano il caso di dati
ad 8 bit; il caso di formati a 16 e a 32 bit, a parte qualche complicazione dovuta al maggior numero di cifre binarie si può sempre ricondurre ai casi visti.