
Da diversi anni, le cosiddette tecniche soft-computing si stanno affiancando ai più tradizionali approcci di programmazione. La loro diffusione in ambito embedded, sta via via crescendo in conseguenza dei notevoli risultati ottenuti anche sul campo.
La progettazione dei sistemi embedded è ormai molto diversa dalla programmazione dei calcolatori. I programmatori per PC sono abituati a standard di memoria quasi illimitata e a comodi ambienti di interfaccia e di debug; al contrario, un programmatore embedded deve far fronte a microcontrollori che devono funzionare con risorse limitate: basse potenze, piccole dimensioni, della memoria di programma e di lavoro, sono fattori comuni a questo tipo di sistemi.
L’evoluzione del mercato richiede tuttavia una gamma sempre più ampia di dispositivi “intelligenti”, intesi come sistemi in grado di reagire in modo adeguato al mutare delle situazioni, senza l’input dell’utente. Per esempio, ai sistemi elettronici di controllo, si richiede sempre più spesso di essere “fault-tolerant”, ovvero di essere grado di fornire il loro servizio in situazioni estreme, come, nel caso di avaria o di perdita di prestazioni di un elemento del sistema stesso. Attualmente, la maggior parte dei sistemi embedded utilizza metodologie di elaborazione hard computing, cioè algoritmi e modelli computazionali deterministici. La capacità decisionale di tali sistemi dipende strettamente da quanto, nella fase di sviluppo, il progettista sia stato capace di includere nel firmware la tolleranza alla variabilità dei dati cui il sistema risulterà sottoposto quando funzionerà in campo. Negli ultimi decenni, a questo tradizionale paradigma di programmazione, si stanno affiancando in modo sempre più massiccio, le cosiddette tecniche Soft Compuntig. Con questo termine si designano tecnologie per la modellizzazione di sistemi complessi: reti neurali, sistemi fuzzy e algoritmi genetici, attraverso le quali è possibile affrontare in modo efficiente problemi in vari domini applicativi come routing, controllo, scheduling, allocazione ottimale di risorse, identificazione di sistemi, analisi di immagini, etc... Soft computing è in sostanza un termine coniato per distinguere una vasta serie di metodologie ispirate a modelli biologici, come il cervello (reti neurali) e suoi meccanismi decisionali (logica fuzzy), o i meccanismi evolutivi (algoritmi genetici), imitandone il funzionamento e soprattutto le peculiarità, da quelle metodologie a base matematica e logica (algoritmi), contrassegnate con il termine hardcomputing.
Il punto di forza delle implementazioni soft computing, è rappresentato dalla capacità di apprendere e dalla capacità di generalizzare: queste due peculiarità, sono particolarmente interessanti per lo sviluppo di sistemi embedded, in quanto consentono di soddisfare uno dei requisiti fondamentali di tali sistemi: operare senza essere assistiti dall’uomo. Il soft computing si distingue inoltre dalle tecniche convenzionali hard computing per il fatto di tollerare l’imprecisione, l’incertezza e le verità parziali. Il suo principio guida è quello di sfruttare questa tolleranza per ottenere trattabilità, robustezza e contenimento delle risorse computazionali necessarie per risolvere i problemi affrontati. L’approccio soft computing è infatti in grado di gestire anche situazioni non previste nella fase di sviluppo, grazie alla sua capacità intrinseca di generalizzare la conoscenza acquisita alla stessa maniera di come un essere umano è capace di reagire più o meno efficacemente rispetto a situazioni che non aveva mai affrontato prima (di cui cioè non aveva esperienza pregressa). Le altre esperienze immagazzinate concorrono a derivare una soluzione che meglio si adatta al problema sconosciuto. In particolare, le metodologie soft computing conferiscono al sistema embedded caratteristiche di autonomia, facilità di modellazione, economicità funzionale: grazie a queste caratteristiche, i sistemi non solo risultano più versatili e affidabili, ma consentono anche di ridurre i costi di sviluppo e progettazione. C’è infine da dire, che per una vasta tipologia di problemi, spesso non vi è alcun approccio di tipo tradizionale per giungere (in tempi ragionevoli!) ad una soluzione: questo “costringe” per così dire, all’applicazione di soluzioni “intelligenti”. Risolvere infatti alcune tipologie di problemi utilizzando i metodi classici, basati su algoritmi di tipo esaustivo, può essere molto difficile, se non a volte del tutto impossibile. L’approccio migliore consiste allora nell’impiegare le tecniche cosiddette euristiche, ovvero non convenzionali, di soft computing. La particolarità di queste tecniche è che non garantiscono con certezza dei buoni risultati, ma anzi potrebbero addirittura in alcuni casi non trovare affatto delle soluzioni; in generale però, si rilevano più efficienti e semplici da implementare delle tecniche classiche. Nel seguito di questo articolo, ci soffermeremo su uno dei tre pilastri del soft computing: quello degli Algorimi Genetici. Queste tecniche, per le loro caratteristiche, ben si prestano (con opportuni adattamenti) ad essere implementati anche su piccoli microcontrollori.
Algoritmi Genetici
Verso l’inizio degli anni ‘60, molti ricercatori si interessarono dei sistemi naturali, convinti che l’evoluzione della specie sia una guida robusta e ben verificata per modellare i fenomeni che si auto-organizzano. Gli organismi viventi sono, infatti, ottimi risolutori di problemi e le loro abilità sono il risultato dell’evoluzione naturale. Partendo da questi presupposti, J. Holland , propose ed elaborò i cosiddetti Algoritmi Genetici, con lo scopo di cercare di copiare gli strumenti ed il funzionamento dell’evoluzione delle specie. Nelle specie biologiche, gli individui più idonei, sono favoriti per la sopravvivenza e la riproduzione; l’evoluzione di una specie è regolata essenzialmente da due processi fondamentali: la selezione naturale e la riproduzione sessuale. La selezione naturale determina quali individui di una popolazione sopravvivono abbastanza per riprodursi (per esempio quelli in grado di riconoscere i predatori e di sfuggirgli), mentre la riproduzione sessuale determina la ricombinazione del materiale genetico dei genitori. Basandosi sull’analogia biologica, negli algoritmi genetici si assume che una possibile soluzione di un problema possa essere rappresentata con un set di parametri, detti geni, i quali formano una stringa di valori detta cromosoma (figura 1).

Figura 1: cromosoma digitale, l’elemento base di un algoritmo genetico.
In breve, un algoritmo genetico è un algoritmo iterativo che opera su una popolazione di individui. I membri della popolazione, che codificano soluzioni candidate di un dato problema, sono valutati tramite una funzione denominata fitness, che determina quanto bene essi risolvano il problema e i migliori individui sono selezionati per la riproduzione. Gli individui della nuova popolazione sono creati utilizzando semplici operatori random, ispirati alla riproduzione sessuale e alla mutazione. Il ciclo di valutazione, selezione, riproduzione sessuale e mutazione è iterato per un certo numero di generazioni, fino al raggiungimento di un dato criterio di arresto.
Come è strutturato di un algoritmo genetico?
Il primo passo per implementare un algoritmo genetico è quello di schematizzare il problema che dobbiamo affrontare, trovando una rappresentazione per le possibili soluzioni che utilizzi una stringa di simboli, in genere binaria. In un algoritmo genetico per un certo problema, si ha un popolazione di soluzioni: questa popolazione subisce un’evoluzione sotto forma di selezione naturale. Ad ogni generazione le soluzioni relativamente buone sopravvivono e si riproducono, mentre le soluzioni relativamente cattive, muoiono per essere poi sostituite dai figli delle soluzioni buone. La valutazione dei singoli individui (ossia delle soluzioni) viene effettuata mediante una funzione obiettivo che gioca il ruolo che in natura è ricoperto dall’ambiente. Esaminiamo nel dettaglio un algoritmo genetico facendo riferimento al diagramma di flusso di figura 2.
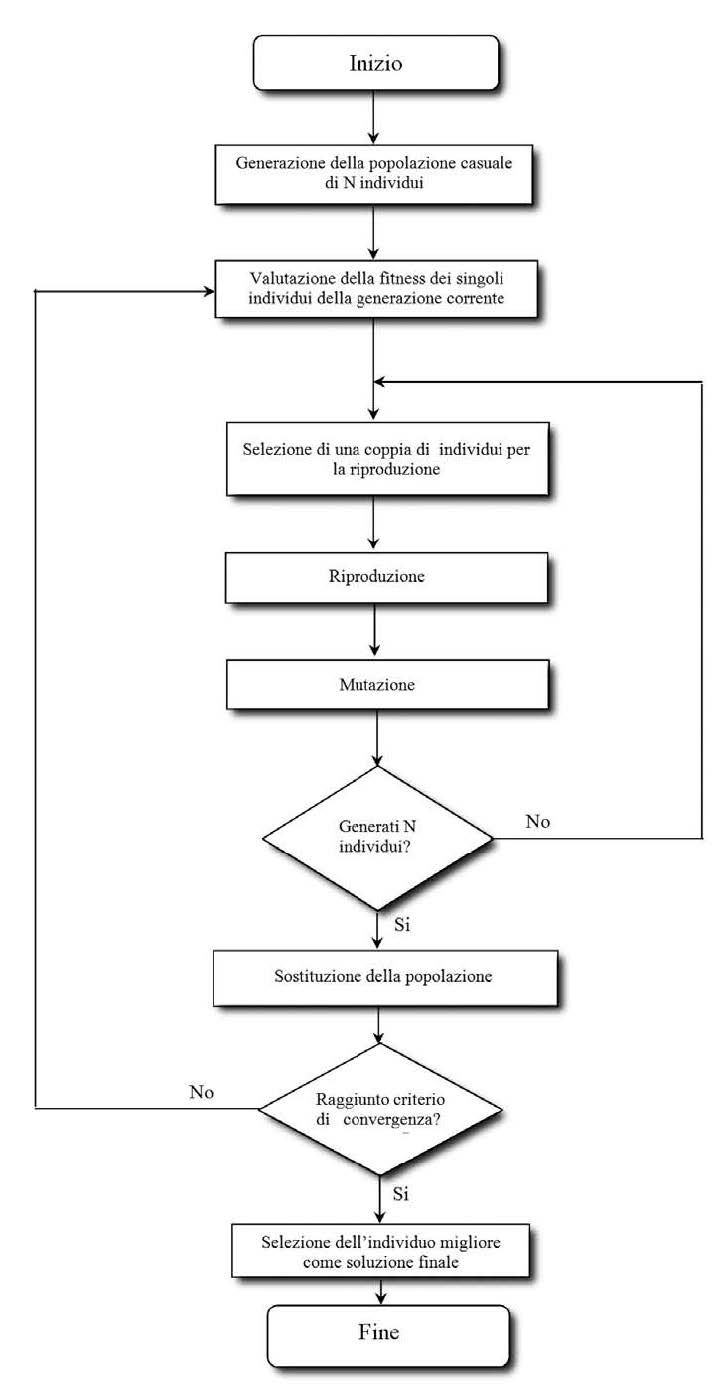
Figura 2: un algoritmo genetico.
Dapprima viene generata una popolazione, ovvero un gruppo di possibili soluzioni candidate; ogni soluzione è chiamata individuo. In generale la popolazione iniziale è un gruppo di possibili soluzioni che vengono generate in maniera casuale. Successivamente inizia un processo iterativo che applica un gruppo di operatori genetici: l’operatore selezione, l’operatore di crossover, l’operatore mutazione. Un algoritmo genetico gestisce una popolazione p(t) di N individui. In generale, il processo iterativo si ferma, quando viene raggiunto il numero massimo di generazioni che si vogliono prendere in considerazione o quando viene soddisfatto un opportuno test di convergenza. Durante l’iterazione t, ogni individuo, viene valutato mediante il calcolo di una funzione che fornisce una misura della bontà della soluzione: questo fatto permette di valutare se una soluzione sia migliore di un’altra. Durante questa fase, viene deciso quali soluzioni-individui sopravvivranno e si riprodurranno. Ovviamente, poiché vorremmo trovare la soluzione migliore, la scelta della funzione obiettivo è molto importante. La fase di selezione è basata sulla analisi della funzione obiettivo: infatti la selezione viene fatta in modo che gli individui con una fitness migliore abbiano più probabilità di riprodursi. In questo modo, poiché un nuovo individuo viene generato da un altro scelto nella popolazione precedente P(t), gli individui con basso valore della fitness (se il nostro scopo è quello di minimizzare la funzione obiettivo), generano un numero maggiore di figli: la ricerca della soluzione migliore avviene così in maniera più decisa nell’intor no delle soluzioni buone, piuttosto delle soluzioni cattive. L’operatore selezione colloca nella nuova popolazione P(t+1) un numero sempre maggiore di copie degli individui con fitness sotto la media degli individui della popolazione P(t) (se l’obiettivo fosse stato quello di massimizzare la funzione obiettivo, si sarebbero scelti gli individui con valori della fitness sopra la media , naturalmente). Proporzionalmente al valore di fitness fi, agli individui sono associate le probabilità di selezione:
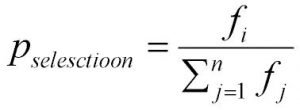
utilizzate per costruire una sorta di “roulette” di probabilità. Per esempio, se la popolazione è composta da 4 individui A1, A2, A3 e A4, con le rispettive probabilità di selezione psA1 = 0,14, psA2 = 0,16, psA3 = 0,2 e psA4 = 0,5 la corrispondente roulette avrà la forma mostrata in figura 3.
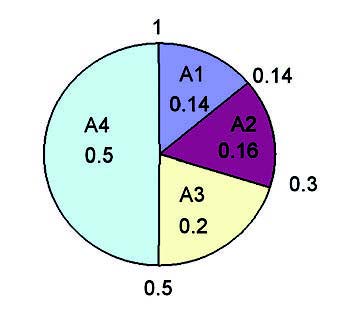
Figura 3: la roulette delle probabilità.
L’operatore di selezione c genera un numero casuale compreso tra 0 e 1 e seleziona l’individuo la cui fetta di roulette ne contiene il valore. Per esempio se c = 0,7, con riferimento alla figura 3, l’individuo selezionato è A4 poiché la fetta di roulette relativa ad A4 specifica i valori dell’intervallo [0,5; 1] e il valore di c ricade in tale intervallo. Quando un individuo è selezionato ne viene creata una copia e quest’ultima viene inserita nel cosiddetto, mating pool (piscina di accoppiamento). Una volta che il mating pool è riempito con n copie di individui della popolazione P(t=0), gli individui della nuova popolazione P(t+1) sono ottenuti come loro discendenti attraverso gli operatori di crossover, e mutazione. L’operatore di selezione determina, dunque, quali individui della vecchia popolazione hanno la possibilità di generare dei discendenti e gioca, nel contesto dell’algoritmo genetico, il ruolo della selezione naturale per gli organismi viventi. Dopo la fase di selezione, vi è una fase di ricombinazione; durante questa fase, vengono introdotti due nuovi operatori: crossover e mutazione. Esistono in letteratura diversi tipi di operatori di crossover: i più noti sono il crossover sessuato e il crossover asessuato. Il primo operatore (figura 4) è attivo con una probabilità ps, indipendente dall’individuo specifico su cui è applicato.
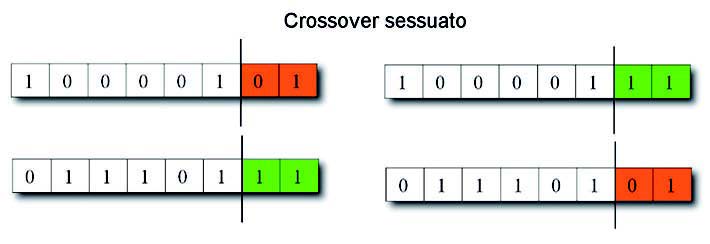
Figura 4: un esempio di crossover sessuato.
Esso prende come ingresso due individui (genitori), scelti casualmente e li combina per generare due figli. La combinazione viene effettuata mediante la scelta con probabilità uniformemente distribuita, di un punto di crossover nelle stringhe dei due genitori e poi scambiando tutti i valori a destra di questo punto: in questo modo si ottengono due nuovi cromosomi a cui corrispondono figli diversi dai genitori, anche se somiglianti. Chiaramente se i genitori sono identici, i figli saranno a loro volta identici ai genitori e proprio questo garantisce la convergenza della popolazione verso la configurazione migliore. L’operatore viene fatto agire finché non si ottiene un numero di figli sufficienti a rimpiazzare tutti i genitori, ottenendo così una nuova generazione. La probabilità ps è generalmente minore di 1 (in genere è compresa tra 0,7 e 0,9) in modo tale che non sempre i genitori creino dei figli diversi: questo dovrebbe garantire la sopravvivenza nella generazione futura di alcuni individui della generazione attuale. La tendenza attuale, tuttavia, è quella di applicare sempre l’operatore di riproduzione e salvare comunque nella generazione futura alcuni individui: i migliori di quella attuale. L’operatore di crossover asessuato (figura 5) scambia invece parti di stringhe dello stesso individuo.
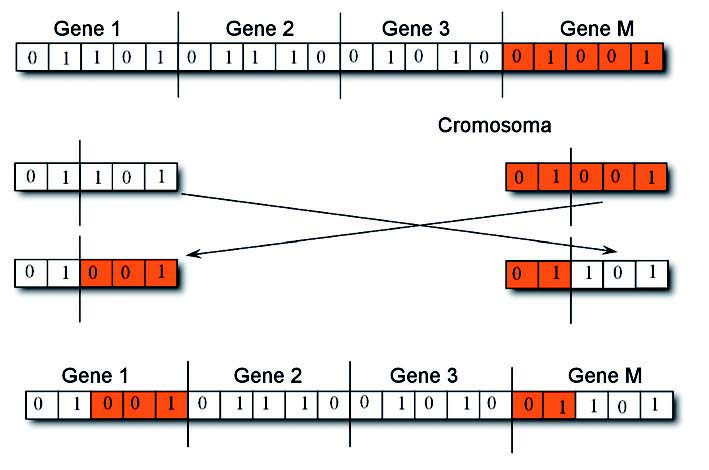
Figura 5: un esempio di un crossover asessuato.
Una volta che due geni di un unico cromosoma siano stati selezionati (si scelgono due geni a caso come nel caso dell’operatore di crossover sessuato erano stati scelti due cromosomi) viene poi individuato il punto di crossover con distribuzione uniforme. Utilizzando l’operatore di crossover asessuato, le porzioni di gene tra il punto di crossover e la fine del gene vengono scambiate. Nel caso dell’operatore asessuato non esiste più il concetto di stretta somiglianza dei figli ai genitori. In particolare, se è vero che con il crossover sessuato, da genitori identici si ottengono figli uguali ai primi, in questo caso da un genitore si ottiene generalmente un figlio diverso. Quindi, nel caso della riproduzione sessuata, quando la popolazione tende a convergere si ottengono poche o nessuna soluzione diversa da quella verso cui sta convergendo, limitando così la ricerca durante le ultime generazioni. Al contrario, con la riproduzione asessuata si ottengono sempre e comunque numerose soluzioni diverse, permettendo così una ricerca più completa sfruttando al meglio anche le ultime generazioni. L’operatore mutazione (figura 6) infine provoca, con una percentuale pm il cambio di un valore di un allele (cioè un bit) in un gene scelto casualmente.
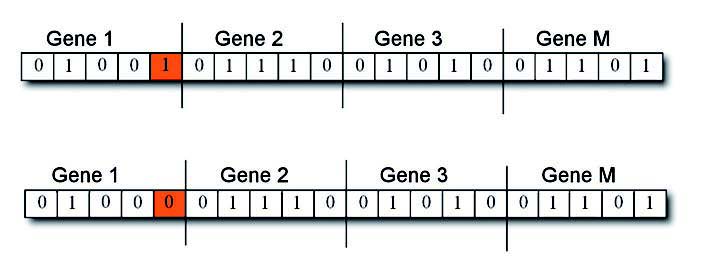
Figura 6: operatore mutazione applicato ad un cromosoma.
Questo operatore introduce le variazioni fondamentali nella popolazione per garantire la possibilità di esplorare l’intero spazio di ricerca indipendentemente dalla popolazione iniziale.
Un esempio di algoritmo genetico
A titolo esplicativo, supponiamo di voler massimizzare la funzione (figura 7):
![]()
con n compreso tra 0 e 63 - tramite un algoritmo genetico. Il primo passo da fare è la codifica del parametro n: ad esempio è possibile codificare n con una stringa di 6 bit coincidente con la sua rappresentazione in binario.
000000
000001
000010
000011
………
111111
L’algoritmo genetico parte generando una popolazione di N individui, ognuno dei quali è rappresentato da un diverso valore della variabile n.Ad esempio si può considerare una popolazione casuale di 5 individui; per ciascuno degli individui considerati si calcola la fitness in base al modello del problema da risolvere. Nel caso in esame la fitness può essere definita in modo semplice attraverso il valore assunto dalla funzione in corrispondenza del valore n associato all’individuo.
000000 f(0) = 0
000111 f(7) = 399
000011 f(3) = 183
011100 f(28) = 1008
010000 f(16) = 768
Il passo successivo consiste nella scelta degli individui da riprodurre, scelta che deve essere effettuata in modo tale da favorire individui con più alto fitness senza però escludere completamente gli altri per garantire uno sfruttamento ottimale del materiale genetico della popolazione. Un modo molto semplice per fare ciò è assegnare a ciascun individuo una probabilità di riproduzione pari al rapporto percentuale tra il suo fitness e la somma dei fitness di tutti gli individui della generazione.
000000 0 f(0) = 0 p1 = 0%
000111 7 f(7) = 399 p2 = 16.92%
000011 3 f(3) = 183 p3 = 7.76%
011100 28 f(28) = 1008 p4 = 42.75%
010000 16 f(16) = 768 p5 = 32.57%
somma = 2358
A questo punto possiamo passare alla fase di crossover sessuato, che in pratica consiste nello scambio di parti delle stringhe dei genitori per formare gli individui figlio. Ipotizzando un single point crossover, si tagliano le stringhe in una posizione scelta a caso per produrre due segmenti testa e due segmenti coda. I segmenti coda sono poi scambiati per produrre due nuovi cromosomi di lunghezza completa. Il crossover non è abitualmente applicato a tutte le coppie di individui selezionati per l’accoppiamento, ma con una certa probabilità (compresa tra 0,7 e 0.9). Se il crossover non è applicato i figli sono generati semplicemente duplicando i genitori. Supponiamo di selezionare per la riproduzione il quarto ed il quinto individuo e di incrociarli per esempio sul terzo bit. Per la seconda iterazione di riproduzione potranno essere selezionati il secondo e terzo individuo i cui cromosomi possono essere scambiati per esempio dal quarto bit:
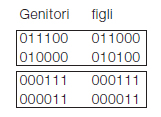
Notiamo che, nell’accoppiamento tra secondo e terzo individuo,siccome le parti a sinistra del punto di taglio sono identiche,il crossover non ha alcun effetto. Questa eventualità è più comune di quanto si possa immaginare, specialmente quando, avanti con le generazioni, la popolazione sia piena di individui tutti buoni e quasi identici tra di loro, ovvero quando la popolazione sta convergendo. In ogni caso il cromosoma dei figli è successivamente soggetto a mutazione, ovvero ogni gene è modificato con una probabilità bassa (tipicamente 0.001). La mutazione serve ad inserire un po’ di casualità nella ricerca per assicurare che nessun punto nello spazio abbia probabilità nulla di essere esaminato. Nell’esempio in esame facendo riferimento alla prima copia di figli generati si supponga di mutare solo il primo bit del primo figlio
111000
010100
Il processo di generazione dei figli continua fino a quando il numero di individui generati uguaglia il numero iniziale di individui nella popolazione. In questo modo si completa la nuova generazione e il processo si ripete attraverso le fasi di valutazione, selezione, incrocio, mutazione, fino a che non si raggiunge il criterio di stop desiderato. In generale, ad ogni nuova generazione la fitness media della popolazione dovrebbe subire un incremento. Iterando lo stesso processo più volte,si arriva ben presto a un punto in cui fa la sua comparsa un individuo associato alla soluzione ottima del problema. Si può decidere di fermare l’algoritmo, quando si raggiunge un determinato grado di idoneità della fitness oppure quando è stato analizzato un numero prefissato di generazioni. In alternativa si può interrompere il GA quando l’incremento di fitness tra una generazione e la successiva è inferiore ad una predeterminata quantità.
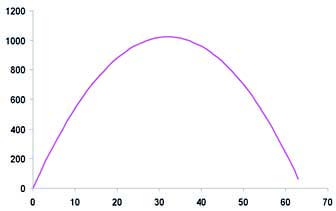
Figura 7: la funzione -m2+64m.




