
Negli ultimi anni le tecniche di controllo predittivo, basate su modello, hanno suscitato interesse crescente nel settore del controllo di processo poiché possono consentire un miglioramento di prestazioni rispetto alle tecniche convenzionali. In questo articolo sono trattati alcuni algoritmi di controllo predittivo non lineare di cui sono state confrontate le prestazioni tramite test degli stessi su di un sistema non lineare costituito da un robot planare a due link.
Le tecniche di controllo predittivo fanno uso di un modello del sistema per pianificare la legge di controllo. Questa viene determinata tramite minimizzazione di un indice di costo che esprime in maniera formale gli obiettivi da conseguire sul sistema controllato. Tale indice si compone di una parte che valuta l’errore quadratico tra uscita futura desiderata e uscita predetta e una parte che tiene conto dello sforzo di controllo dell’ingresso. La minimizzazione dell’indice può tener conto anche di eventuali vincoli sul processo o sulle variabili di controllo.
Il presente articolo tratta il controllo predittivo di sistemi non lineari, per i quali occorre risolvere in tempo reale un problema di ottimizzazione non lineare vincolata. La complessità del problema è legata alla dinamica del sistema, al numero di variabili di decisione ed al tipo di vincoli imposti. Si rende necessario derivare la legge di controllo predittivo basandosi su un modello non lineare del sistema. Questo approccio richiede elevate potenze di calcolo per risolvere in tempo reale problemi di ottimizzazione vincolata non lineare. Il Controllo Predittivo Basato sul Modello (Model-based Predictive Control, MPC) si differenzia dal controllo convenzionale (ad esempio, di tipo PD) perché è più adatto per inseguire una traiettoria di riferimento (target), in particolare consente di prevederne l’andamento. Nel caso del controllo convenzionale, infatti, il sistema di regolazione è in grado di rispondere a una variazione del target solo dopo che questa si è manifestata. Il controllo predittivo, invece, riesce a vedere la variazione del target prima che si manifesti e quindi reagisce ad essa in anticipo. Le caratteristiche che rendono il controllo predittivo interessante per gli impieghi pratici sono le seguenti [1]:
- il controllo predittivo non è ristretto a sistemi single-input, single-output (SISO), ma può essere applicato a sistemi multi-input, multi-output (MIMO);
- il controllo predittivo può essere messo a punto sia per processi lineari che non lineari;
- il controllo predittivo è una metodologia che può manipolare vincoli (constraints) sul processo in modo sistematico durante il progetto del Poiché nelle applicazioni pratiche i vincoli sul processo sono molto comuni, questa caratteristica è molto importante ed è uno degli aspetti più interessanti del controllo predittivo;
- il controllo predittivo è una metodologia “aperta”: all’interno di questo campo ci sono vari modi di progettare un controllore predittivo;
- il controllo predittivo può essere usato per controllare una grande varietà di processi, senza che il progettista debba prendere speciali precauzioni:
può essere usato per controllare processi con dinamica semplice così come processi con dinamica complessa, per processi a fase non minima e per processi instabili ad anello aperto.
Poiché i controllori predittivi appartengono alla classe di metodi di progetto basati sul modello, nel progetto di un sistema di controllo si distinguono la fase di modellazione del processo e quella di progetto del controllore. Il controllo predittivo fornisce una soluzione solo per la parte di progetto del controllore; il modello del processo deve essere ottenuto con altri metodi.
CONTROLLO PREDITTIVO NON LINEARE
Negli ultimi anni, grazie allo sviluppo della tecnologia informatica, il controllo predittivo non lineare (Nonlinear Model-based Predictive Control, NMPC) è diventato una tecnica popolare per affrontare problemi di controllo complessi.
I concetti fondamentali su cui si basa il controllo predittivo, in particolare quello non lineare, sono i seguenti ([2], [3]):
- l’uso di un modello per la predizione dell’evoluzione futura del sistema reale;
- il calcolo on-line della sequenza di controllo ottima ottenuta minimizzando un indice di prestazione definito che quantifica il comportamento desiderato;
- l’applicazione dell’orizzonte mobile (Receding Horizon, RH): solo il primo valore della sequenza ottima calcolata
viene applicato al processo; quindi l’orizzonte viene traslato di un campione nel futuro e viene calcolata una nuova sequenza.
IL MODELLO E IL SISTEMA
Nel controllo predittivo il modello del sistema è espressamente usato per calcolare la legge di controllo, per cui il modello dovrebbe essere il più accurato possibile. Se si ha una conoscenza fisica approfondita del funzionamento del sistema, il modello può essere espresso in forma di spazio di stato per mezzo di equazioni, altrimenti si devono acquisire informazioni su di esso basandosi sui dati sperimentali. Lo schema a blocchi del controllo predittivo è riportato in figura 1 dove:
- r(k) rappresenta l’andamento di uscita desiderato (setpoint o target);
- y(k) rappresenta l’andamento di uscita ottenuto;
- u*(k) rappresenta la sequenza di ingresso ottima;
il blocco “sistema” rappresenta la dinamica ad anello aperto del sistema reale.
LA LEGGE DI CONTROLLO OTTIMA
La sequenza di controllo ottima u*(k) (figura 1) è determinata come risultato di un problema di ottimizzazione vincolato ad ogni istante di campionamento.
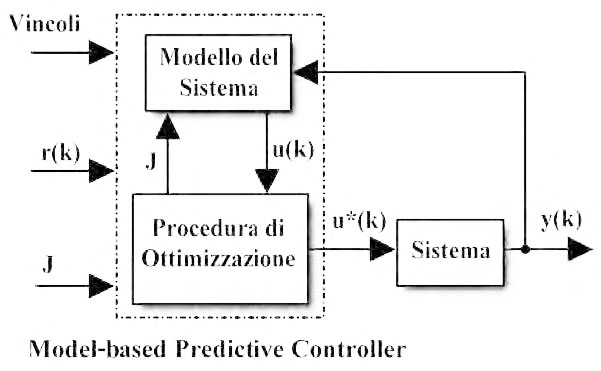
Figura 1: la sequenza di controllo ottima
Tutte le specifiche sono quantificate tramite un indice di costo (J) composto da un termine che valuta l’errore quadratico tra l’uscita futura desiderata e quella predetta all’interno di un orizzonte di predizione definito (che è una finestra di P campioni) e un secondo termine usato per pesare lo sforzo di controllo quantificato dalla sequenza degli incrementi di ingresso all’interno di un orizzonte di controllo (che è una finestra di M campioni). Il controllo predittivo è usato, soprattutto, quando sono presenti dei vincoli (constraints) sul processo. Questi vincoli sono legati ai valori massimo e minimo e al tasso di variazione delle variabili di ingresso (variabili manipolate) e di uscita (variabili controllate). I vincoli sulle variabili di ingresso tengono conto delle limitazioni pratiche degli attuatori, mentre quelli sulle variabili di uscita possono servire per evitare che il sistema lavori in prossimità di regioni indesiderate. Il tuning di un controllore predittivo si effettua scegliendo la lunghezza dell’orizzonte di predizione P, quella dell’orizzonte di controllo M e i coefficienti di normalizzazione che compaiono nell’espressione dell’indice di costo. I valori di tali parametri vanno scelti seguendo delle linee guida generali (come proposto ad esempio in [1], [4]) e, per tentativi, fino ad ottenere una risposta ragionevole del sistema.
L’ORIZZONTE MOBILE
Un aspetto chiave nel controllo predittivo è l’applicazione della strategia dell’orizzonte mobile (Receding Horizon, RH). In questo approccio solo il primo campione della sequenza ottima calcolata u*(k+j) è applicato al sistema, successivamente l’orizzonte è traslato un campione avanti nel futuro e l’ottimizzazione è ripetuta sulla base dell’informazione di retroazione misurata. La strategia dell’orizzonte mobile è illustrata in figura 2.
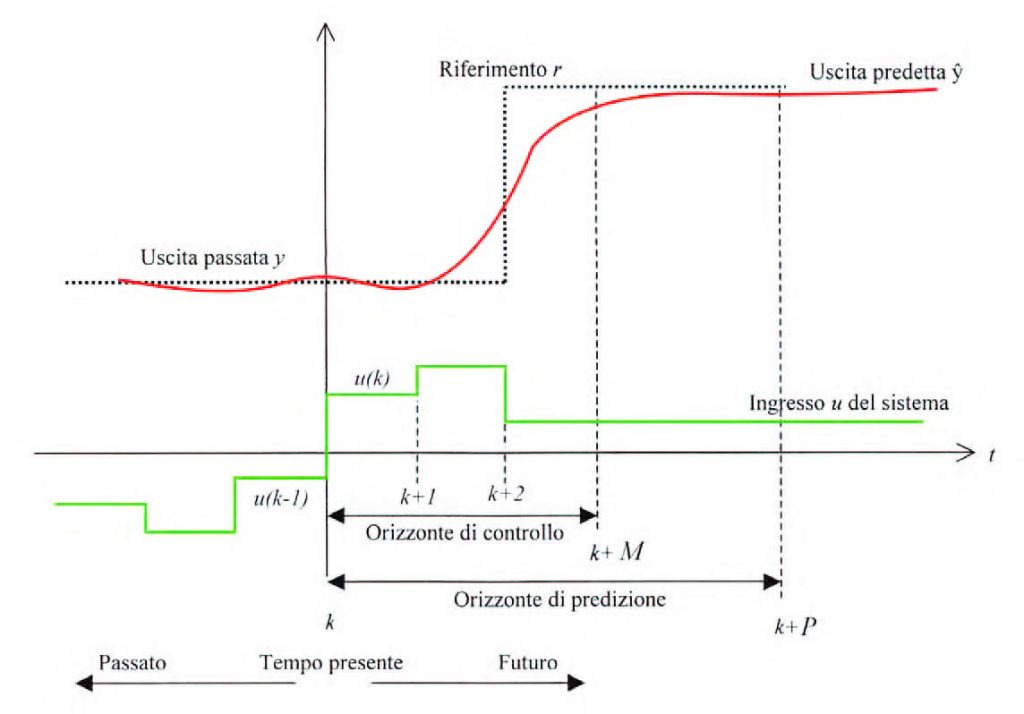
Figura 2: la strategia dell’orizzonte mobile
Le uscite future del processo sono predette all’interno di un orizzonte di predizione di lunghezza P usando il modello del processo. I valori di uscita predetti dipenderanno dall’evoluzione del processo nei vari istanti e dai segnali di controllo futuri che saranno forniti al sistema. Con l’approccio dell’orizzonte mobile, il segnale di controllo viene manipolato solo all’interno dell’orizzonte di controllo M, successivamente viene mantenuto costante al valore assunto alla fine dell’orizzonte di controllo, fino al raggiungimento dell’orizzonte di predizione P. L’approccio dell’orizzonte mobile permette di compensare disturbi futuri o errori di modello. A causa di disturbi o errori di modello l’uscita y(k+1) predetta all’istante t, può essere anche molto diversa dall’uscita y(k) misurata all’istante successivo t+1. All’istante t+1 conviene, quindi, fare una predizione a partire dall’uscita misurata in quest’istante anziché da quella predetta all’istante di campionamento precedente. In tal modo è attivo un meccanismo di retroazione che consente di compensare i problemi derivanti dalla presenza di disturbi o da variazioni parametriche del modello. L’orizzonte al l’interno del quale l’uscita del processo è predetta, di conseguenza, trasla di un campione nel futuro ad ogni istante di campionamento e viene effettuata una nuova ottimizzazione.
ALGORITMI DI CONTROLLO PREDITTIVO NON LINEARE
Gli algoritmi di controllo predittivo non lineare implementati e confrontati sono di seguito descritti. Il primo (indicato con l’acronimo NMPC1) è applicato dagli autori ([5], [6]) al controllo dell’impianto ad energia solare della Plataforma Solar de Almerìa (Spagna). Il secondo (indicato con l’acronimo NMPC2) sfrutta il metodo di ottimizzazione branch-and-bound ed è stato applicato dagli autori ([7], [8], [9]) a vari sistemi, tra cui il controllo di forza di un robot. Il terzo (indicato con l’acronimo NMPC3) sfrutta come tecnica di ottimizzazione un algoritmo evolutivo ed è stato applicato dagli autori ([3], [10], [11], [12]) a diversi sistemi, tra cui una camera climatica.
ALGORITMO NMPC1
La strategia può essere schematizzata con i seguenti passi:
- Inizializzare a zero gli ingressi, calcolare P valori futuri di y usando il modello e calcolare il corrispondente indice di costo
- Per ogni campione futuro i che giace nell’orizzonte di controllo (0 < i < M), aggiungere all’ingresso attuale il massimo valore uMAX ammesso per la variazione dell’ingresso e calcolare la corrispondente funzione di costo J1 (tenere conto dei vincoli sull’ingresso, ossia tosare il segnale relativo nel caso in cui si violi un vincolo). A partire dallo stesso ingresso iniziale sottrarre uMAX e calcolare la corrispondente funzione di costo J2 tenendo conto dei vincoli. Per i campioni con M £ i < P, mantenere il valore attuale dell’ingresso.
- Se la funzione di costo J calcolata al puto precedente (ossia la J1 oppure la J2) è minore del valore attuale di J, sostituire il valore dell’ingresso con quello corrispondente al minimo e assumere il valore della funzione di costo corrispondente come valore attuale. Tornare al passo 2.
- Se l’attuale incremento di ingresso non permette di ottenere una ulteriore minimizzazione di J, moltiplicarlo per un fattore a<1. Se il valore di u è ancora maggiore del minimo consentito umin, tornare al passo 2, altrimenti stop.
La procedura va ripetuta per tutti i campioni della sequenza. I parametri che devono essere scelti dall’utente sono:
- gli orizzonti di controllo e di predizione M e P;
- i coefficienti di normalizzazione;
- il fattore a;
- i valori uMAX e umin usati per variare l’ingresso.
Il diagramma di flusso di questo algoritmo è riportato in figura 3.
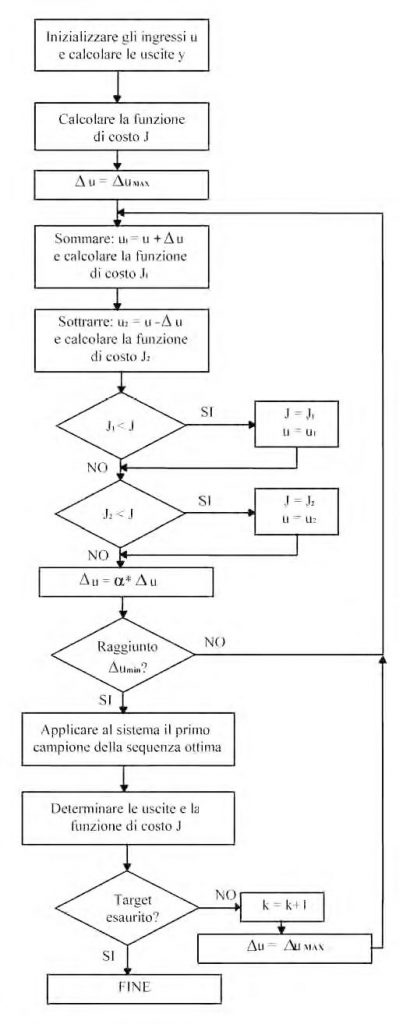
Figura 3: L'algoritmo NMPC1
Tra i parametri che devono essere scelti dall’utente c’è il coefficiente a. La sua scelta è molto importante in quanto una discretizzazione grossolana potrebbe produrre risultati insoddisfacenti (come oscillazioni indesiderate delle variabili di ingresso - chattering), mentre una troppo fine potrebbe richiedere un tempo proibitivo per determinare la soluzione ottima. Un modo per risolvere questi problemi è far variare a in funzione dell’errore di predizione: per errore piccolo conviene mantenere piccolo il valore di a per limitare la ricerca nell’intorno dell’origine mentre per errore grande, il valore di a dovrebbe essere grande per consentire un recupero veloce.
ALGORITMO NMPC2
L’algoritmo è basato sul metodo di ottimizzazione branch-and-bound (B&B). La procedura di ottimizzazione esplora solo un sub-set delle possibili alternative di controllo riducendo, quindi, il tempo necessario alla determinazione della sequenza di controllo ottima. Le due operazioni di base del metodo sono:
- branching: consiste nel dividere il set delle soluzioni in sub-set;
- bounding: stabilire dei limiti sul valore dell’indice di costo in relazione al sub-set delle possibili soluzioni. Questi limiti eliminano quei sub-set che non contengono una soluzione Quando le azioni di controllo sono discretizzate, il metodo B&B può essere applicato al controllo predittivo, come mostrato in figura 4. L’indice di costo viene calcolato per i diversi nodi che vengono esplorati. Si applica la strategia dell’orizzonte mobile: ad ogni passo di campionamento gli orizzonti vengono spostati di un passo e si ripete l’ottimizzazione. All’interno dell’orizzonte di controllo, gli ingressi vengono variati per determinare la sequenza ottima, mentre oltre tale orizzonte sono mantenuti al valore precedente fino a che non si raggiunge l’orizzonte di predizione. Pertanto saranno esplorati nuovi rami solo all’interno dell’orizzonte di controllo.
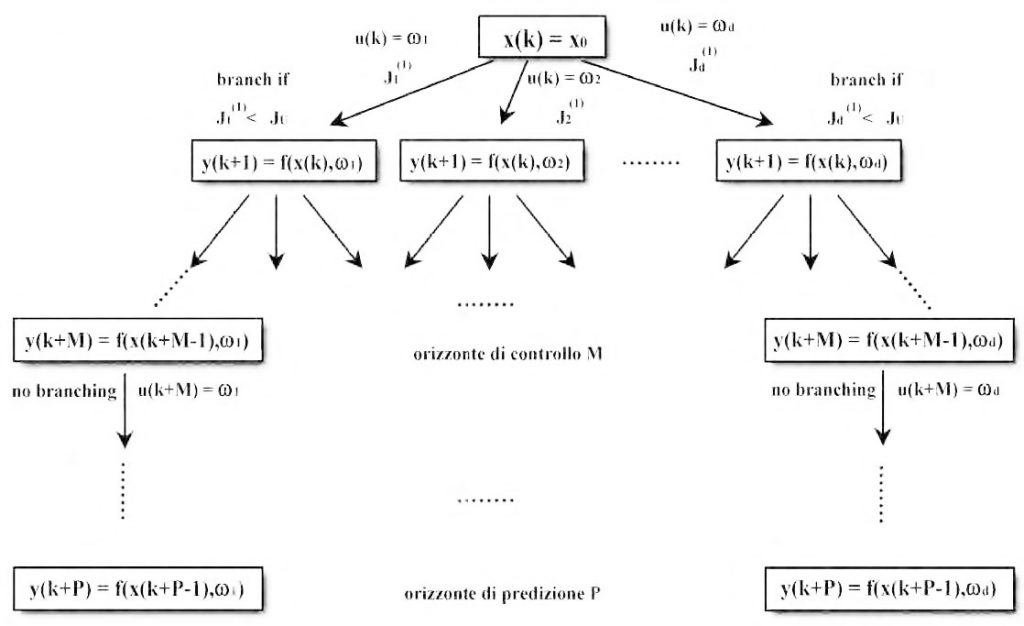
Figura 4: applicazione del B&B al Controllo Predittivo.
L’applicazione del branching da solo comporterebbe l’esplorazione dell’intero albero, cosa proibitiva dal punto di vista computazionale. Per ridurre il numero di alternative si applica il bounding: un particolare ramo viene esplorato solo se il costo cumulativo relativo ad esso è minore di un upper bound del costo totale. Questa tecnica ha tre vantaggi principali sugli altri metodi di ottimizzazione non lineare:
- si trova sempre un minimo globale;
- l’algoritmo non ha bisogno di ipotesi sullo stato iniziale del sistema, quindi le sue prestazioni non sono influenzate negativamente da un’errata inizializzazione;
- il metodo B&B gestisce implicitamente i vincoli, infatti in presenza di vincoli migliora l’efficienza del bounding.
Oltre alla complessità computazionale, il più grande inconveniente dell’approccio descritto è la restrizione delle possibili azioni di controllo a un set di alternative discrete molto ridotto. Questa discretizzazione può causare oscillazioni dell’uscita (chattering). Per evitare quest’effetto indesiderato si può adottare una strategia in cui le alternative di controllo sono spaziate in maniera variabile, utilizzando un fattore moltiplicativo 0 £ a £ 1. Esso deve essere tale che quando il sistema è in condizioni di regime le alternative di controllo devono avere ampiezza ridotta per facilitare la convergenza al valore ottimo, mentre quando sono predette grosse variazioni, le alternative di controllo devono essere ben spaziate per consentire una risposta veloce. Il calcolo di a è stato effettuato, come proposto in [7], sulla base dell’errore predetto tra il riferimento e l’uscita del sistema e sulla base della variazione dell’errore. Quando questi parametri sono entrambi piccoli, il sistema è vicino alla condizione di regime e a dovrebbe tendere a zero per ridurre le oscillazioni; quando sono entrambi grandi, è necessario che a tenda a 1.
ALGORITMO NMPC3
L’algoritmo sfrutta come tecnica di ottimizzazione un Algoritmo Evolutivo (Evolutionary Algorithm, EA) ossia una tecnica che implementa il principio biologico dell’evoluzione della specie in una popolazione, combinata con i meccanismi biologici di incrocio (crossover) e mutazione, per guidare una popolazione di potenziali soluzioni di un problema di ottimizzazione verso la regione più promettente dello spazio di ricerca. Un EA lavora con una popolazione di individui: ogni individuo è chiamato cromosoma. Un cromosoma rappresenta una soluzione potenziale al problema e comprende una stringa di variabili che rappresentano le variabili decisione del problema di ottimizzazione. Un EA mantiene una popolazione di cromosomi e usa, per generare le successive generazioni di popolazione, gli operatori genetici di selezione (rappresenta l’attitudine alla sopravvivenza degli individui migliori ed è quantificata da una misura di fitness che rappresenta la funzione obiettivo), crossover (rappresenta lo scambio di materiale genetico (mating)), mutazione (rappresenta l’introduzione casuale di nuovo materiale genetico). Dopo alcune generazioni l’EA produce una popolazione di soluzioni di alta qualità per il problema di ottimizzazione. L’implementazione di un EA può essere riassunta nei seguenti passi:
- inizializzazione casuale di una popolazione di soluzioni;
- calcolo della funzione fitness per ogni soluzione;
- selezione delle soluzioni migliori per la riproduzione;
- applicazione di crossover e mutazione;
- creazione di una nuova popolazione;
- ripetizione dal passo 2 finché non si raggiunge un certo criterio di La procedura di cui sopra è illustrata in figura 5 [13]. Nella letteratura degli EA è molto comune riferirsi all’ottimizzazione di una funzione fitness anziché alla minimizzazione di un indice di costo per cui, per applicare gli EA al controllo predittivo, si definisce una funzione di fitness pari all’inverso dell’indice di costo. Un cromosoma è generato attraverso la giustapposizione delle sequenze codificate degli incrementi di ingresso. I meccanismi di selezione e riproduzione sono attivi a due diversi livelli dell’ottimizzazione on-line. L’azione a più basso livello riguarda l’ottimizzazione della funzione fitness all’interno dell’intervallo di campionamento k. Avendo a disposizione un tempo di calcolo limitato, dato dal periodo di campionamento, è necessario che le soluzioni buone trovate durante la precedente evoluzione non vadano perse, ma siano usate come punti di partenza per la prossima generazione.
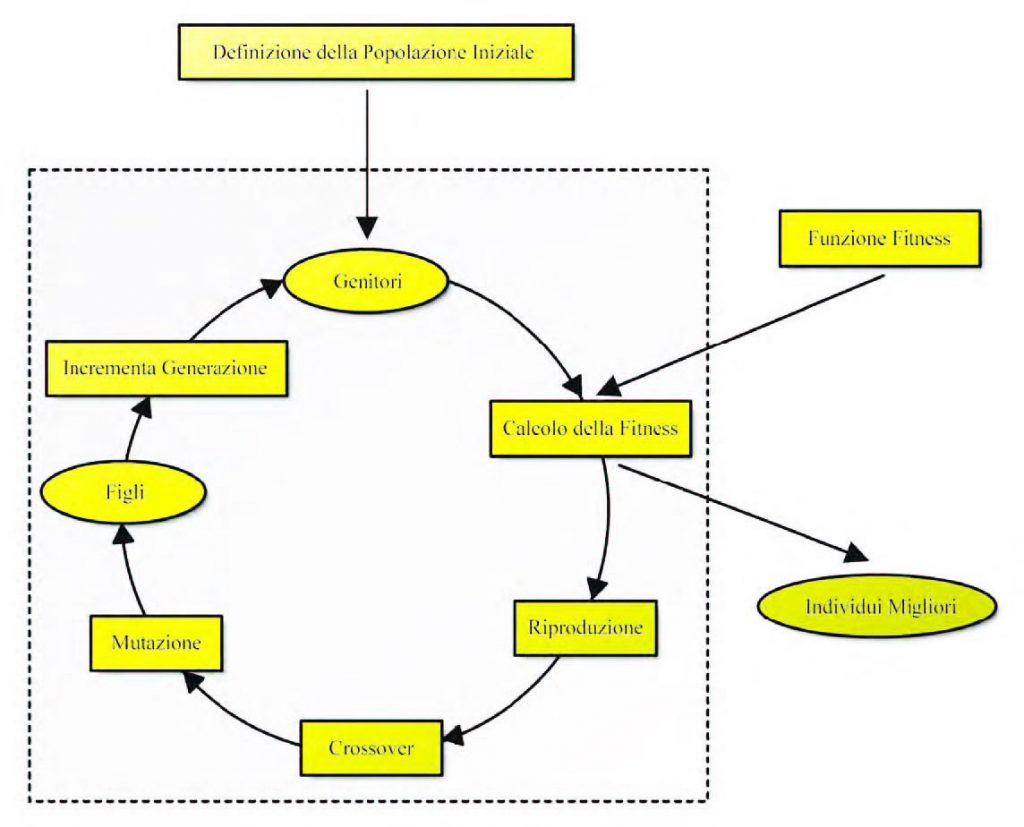
Figura 5: evoluzione artificiale negli algoritmi genetici.
Pertanto i migliori cromosomi della generazione corrente passano invariati alla prossima, assicurando una funzione fitness non decrescente per i migliori individui della popolazione. La parte rimanente della popolazione è generata tramite un meccanismo di rank selection: data una popolazione, gli individui meglio classificati costituiscono un mating-pool, cioè l’insieme dei genitori meritevoli di riprodursi. All’interno del mating-pool sono selezionati casualmente due genitori e vengono creati due figli tramite gli operatori di crossover e mutazione. L’operazione di riproduzione va avanti fin quando non si è generata una nuova intera popolazione. Il secondo livello del meccanismo di selezione agisce come operatore di eredità tra gli intervalli di campionamento k e k+1. I migliori cromosomi calcolati durante il k-esimo intervallo di campionamento possono essere utilizzati come soluzioni di partenza per il prossimo intervallo di campiona- mento. All’inizio del (k+1)-esimo intervallo di campionamento, poiché l’orizzonte è traslato un campione nel futuro, i geni dei migliori cromosomi sono traslati all’indietro di una locazione: in questo modo il primo valore di ogni cromosoma è rimpiazzato dal secondo, il secondo dal terzo e così via. Il valore dell’ultima posizione è mantenuto al valore precedente. I cromosomi traslati rappresentano le soluzioni di partenza nel (k+1)-esimo intervallo di campionamento, i rimanenti sono generati casualmente. Ai cromosomi viene applicato un crossover uniforme con probabilità pc: dati due cromosomi nella generazione corrente, due variabili corrispondenti sono scambiate con probabilità pc. Viene applicata inoltre una mutazione casuale con probabilità pm ad ogni variabile del cromosoma selezionato. La mutazione si applica per evitare una convergenza prematura dei geni verso una soluzione che potrebbe essere un minimo locale e per introdurre delle perturbazioni casuali che consentano l’esplorazione di nuove regioni dello spazio di ricerca. Occorre stabilire un criterio per fermare l’ottimizzazione che tenga conto dei limiti legati all’elaborazione in tempo reale. Il numero massimo di generazioni è, quindi, limitato dal soddisfacimento di questi vincoli. Fissare a priori la durata dell’evoluzione potrebbe ridurre l’efficienza dell’algoritmo, dato che è difficile fissare a priori il numero di generazioni necessarie per trovare soluzioni soddisfacenti. Si è scelto di operare nel modo seguente: l’algoritmo effettua normalmente l’esplorazione di un certo numero di generazioni; se, durante questa esplorazione, il primo gene resta inalterato per un determinato numero di generazioni, l’evoluzione viene fermata. Le prestazioni di un EA sono influenzate dalle dimensioni della griglia in cui può variare la popolazione delle soluzioni. Questo aspetto è molto rilevante nelle applicazioni in tempo reale, dove il tempo di calcolo è limitato. Una discretizzazione troppo grossolana, infatti, genera risultati insoddisfacenti e chattering, mentre una troppo fine richiede un tempo proibitivo per trovare la soluzione soddisfacente. Il problema può essere notevolmente ridotto applicando un fattore di scala alle dimensioni della griglia di ricerca. Il modo di procedere è analogo a quelli visti per i due algoritmi illustrati precedentemente: occorre un fattore di scalatura che sia prossimo a zero per errore piccolo e che sia prossimo a uno per errore grande.
MODELLO DEL ROBOT
Il sistema su cui testare gli algoritmi implementati è un robot planare a due link, la cui struttura è riportata in figura 6 [11].

Figura 6: struttura del robot planare a due link.
Le variabili manipolate sono le coppie applicate ai giunti mentre quelle controllate sono gli angoli ai giunti che definiscono univocamente (per mezzo della convenzione di Denavit- Hartenberg [14]) le coordinate nello spazio operativo px e py dell’utensile applicato all’end-effector. Il controllo del sistema si effettua impostando una certa traiettoria desiderata per l’utensile nello spazio operativo (coordinate xd, yd), dalla quale si determinano gli angoli ai giunti desiderati e da questi il sistema di regolazione ricava le coppie da applicare ai giunti. Applicando tali coppie si ottengono i valori degli angoli ai giunti dai quali poi si risale alla posizione dell’utensile ottenuta nello spazio operativo (px, py).
SIMULAZIONI E RISULTATI
Si riportano ora i risultati ottenuti simulando il funzionamento del robot planare con regolatori PD classici e con controllori predittivi realizzati tramite gli algoritmi illustrati (potete richiedere tutti i grafici delle simulazioni attraverso il servizio MIP indicando il codice MIP che trovate a fine articolo). Nel caso del controllo PD si usano due regolatori indipendenti per le coppie ai giunti secondo gli schemi di controllo decentralizzato nello spazio dei giunti [14]. Nel caso del controllo predittivo l’errore di posizione ai giunti sarà sfruttato per calcolare i parametri a per l’adattamento della griglia di ricerca mentre le coppie da applicare ai giunti saranno calcolate in funzione degli errori di posizione nello spazio operativo. Nelle simulazioni si devono tener presenti le saturazioni degli attuatori che operano sul sistema. Esse corrispondono ai valori massimi, positivi e negativi, delle coppie ai giunti (variabili di ingresso) e del tasso di variazione delle stesse. Nel caso del controllo predittivo tali vincoli vengono gestiti dagli algoritmi, mentre per il controllo PD classico questo non avviene e, per fare in modo che quest’ultimo e il controllo predittivo lavorino nelle stesse condizioni, si possono tosare le coppie quando violano i vincoli sul valore massimo. Il sistema è stato testato supponendo di far muovere il robot in modo che l’utensile disegnasse un rettangolo nello spazio operativo. Con il controllo PD ci si aspettano problemi in corrispondenza dei vertici del rettangolo perché il sistema di regolazione sarà in grado di vedere il cambiamento di direzione solo dopo che si sarà manifestato, pertanto in questi punti si verificheranno delle oscillazioni nell’intorno della traiettoria di riferimento. Con il controllo predittivo questo non avverrà, o avverrà in maniera molto ridotta, in quanto questo tipo di controllo è in grado di vedere la variazione del target prima che essa si manifesti. I risultati saranno confrontati sulla base della qualità delle risposte ottenute e sulla base del costo computazionale valutato in funzione della durata delle diverse simulazioni.
IMPLEMENTAZIONE DELL’ALGORITMO NMPC1
Sono state implementate due versioni di quest’algoritmo: quella con griglia di ricerca a spaziatura fissa (algoritmo NMPC1-A), e quella con griglia adattativa, cioè con parametri adattativi (algoritmo NMPC1-B). Nel caso dell’algoritmo NMPC1-B, i valori di sono stati scelti variabili in funzione dell’errore medio di predizione relativo agli angoli ai giunti, come precedentemente descritto.
IMPLEMENTAZIONE DELL’ALGORITMO NMPC2
Per questo algoritmo si è scelto di applicare ad ogni ingresso tre possibili valori, il che comporta un massimo di 9 possibili coppie di valori. Anche in questo caso sono stati implementati sia l’algoritmo con parametri costanti (algoritmo NMPC2-A), sia quello con parametri a adattativi (algoritmo NMPC2B). Relativamente al NMPC2-B il valore di per ognuna delle coppie ai giunti è legato al minimo tra errore predetto alla fine dell’orizzonte di predizione e variazione dell’errore.
IMPLEMENTAZIONE DELL’ALGORITMO NMPC3
Relativamente all’algoritmo genetico (di seguito indicato con NMPC3) sono stati definiti: il numero di individui che compongono la popolazione, il numero di genitori che compongono il matingpool, il numero delle migliori soluzioni trasmesse all’interno dello stesso intervallo di campionamento, il numero delle migliori soluzioni trasmesse da un intervallo di campionamento al successivo, il numero massimo di generazioni in un intervallo di campionamento, il numero massimo di generazioni in caso di estinzione, la probabilità di crossover e quella di mutazione. Il fattore a per la scalatura della griglia di ricerca è stato calcolato in funzione dell’errore di predizione medio ai giunti.
SIMULAZIONE E DISCUSSIONE DEI RISULTATI OTTENUTI
Effettuando simulazioni utilizzando un orizzonte di controllo M=2 e un orizzonte di predizione P=50 per i vari algoritmi, è stato riscontrato che nel caso del controllo PD la risposta ottenuta si avvicina abbastanza al target quando si è lontani dai vertici del rettangolo desiderato. In corrispondenza di questi punti, invece, si verificano notevoli oscillazioni. La variazione del target viene vista dal sistema di controllo solo dopo che si è manifestata. Per l’algoritmo NMPC1-A la risposta ottenuta coincide con il riferimento quasi per tutta la durata del target. C’è uno scostamento in corrispondenza dei vertici del rettangolo dovuto al fatto che il controllore predittivo vede le variazioni del riferimento prima che si manifestino per cui le variabili di ingresso vengono opportunamente calcolate in anticipo. L’algoritmo NMPC1-B presenta una risposta molto simile a quella ottenuta con NMPC1-A. Le variabili di ingresso presentano, rispetto a quelle dell’algoritmo NMPC1-A, nella parte iniziale della simulazione delle oscillazioni. Nel caso dell’algoritmo NMPC2-A la traiettoria ottenuta oscilla intorno a quella desiderata per tutta la durata della simulazione. Questo comportamento è dovuto all’impiego di un set discreto di alternative di ingresso che fa sì che le coppie ai giunti abbiano un andamento a gradini. Anche in questo caso le variazioni del target, dovute alla presenza dei vertici del rettangolo, sono viste in anticipo dal controllore. Per l’algoritmo NMPC2-B si ha un miglioramento rispetto a NMPC2-A, dovuto all’impiego di uno spazio di ricerca adattativo. Le oscillazioni intorno al riferimento, infatti, risultano meno evidenti rispetto al caso non adattativo. Anche le coppie ai giunti presentano andamenti più regolari. Infine, per l’algoritmo NMPC3 la risposta ottenuta è soddisfacente per tutta la durata della simulazione e le coppie ai giunti presentano un andamento senza variazioni troppo repentine. In tabella 1 è riassunto il confronto tra i diversi algoritmi, in termini di: durata in secondi di ogni simulazione, numero medio di prove fatte dall’algoritmo, in un intervallo di campionamento, prima di trovare la sequenza d’ingresso ottima, errori medi percentuali lungo gli assi x e y, valori quadratici medi degli incrementi delle coppie ai giunti (sforzo di controllo), indice di costo.
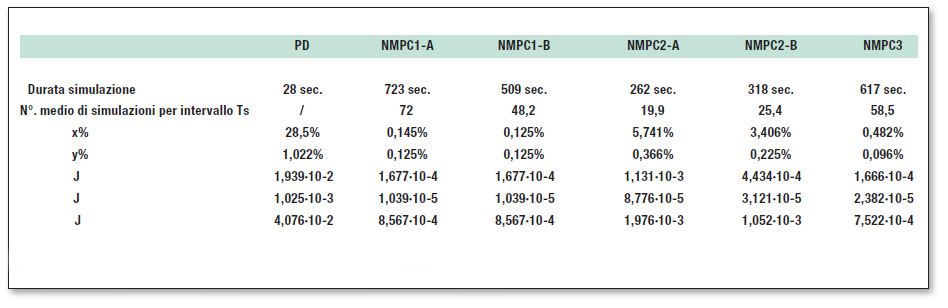
Tabella 1: confronto tra i controllori applicati al robot planare.
Il controllo predittivo fornisce prestazioni di gran lunga superiori rispetto al controllo PD. I due algoritmi NMPC2-A e NMPC2-B sono i meno costosi dal punto di vista computazionale, ma sono i peggiori dal punto di vista dell’errore percentuale lungo gli assi x e y. L’algoritmo NMPC3 si rivela il migliore dal punto di vista dell’errore lungo l’asse y, ma non lungo l’asse x. Gli algoritmi NMPC1-A e NMPC1-B presentano errori percentuali lungo x e y abbastanza piccoli, ma questo si paga con l’aumento del costo computazionale. Per quanto riguarda lo sforzo di controllo, il più costoso relativamente al primo giunto è NMPC2-B mentre il più costoso relativamente al secondo giunto è NMPC2A, ma gli stessi non riescono a fornire prestazioni soddisfacenti in termini di errore. I meno costosi sono NMPC1-A e NMPC1-B i quali riescono a fornire errori piccoli sia su x sia su y. L’algoritmo NMPC3, invece, presenta costo intermedio e consente di ottenere il minimo errore su y, ma non su x.
VARIAZIONE DEGLI ORIZZONTI DI CONTROLLO E DI PREDIZIONE
Analizzando le prestazioni dei diversi algoritmi al variare degli orizzonti di predizione e di controllo, emerge che il costo computazionale aumenta in maniera pressoché lineare con l’allungarsi dell’orizzonte di predizione per gli algoritmi NMPC1-A, NMPC1-B, NMPC3. Per gli algoritmi NMPC2-A e NMPC2-B, invece, si ha un comportamento diverso in quanto il costo computazionale dipende in maniera pesante dal numero di rami da esplorare nell’albero delle soluzioni. In generale l’algoritmo NMPC1-A risulta il più costoso, tranne nel caso di orizzonte < 20, in quanto in questo caso prevale il costo computazionale dei due algoritmi NMPC2-A e NMPC2-B. Questi ultimi risultano i meno costosi per orizzonte >30. Tra i due il meno costoso è ovviamente NMPC2-A in quanto presenta un numero molto limitato di soluzioni da provare.
CONCLUSIONI
Lo studio condotto ha confermato la superiorità del controllo predittivo sui controllori convenzionali sia in termini di errore sulla traiettoria di riferimento che di sforzo di controllo. Il confronto tra gli algoritmi ha portato alla conclusione che un inseguimento accurato della traiettoria di riferimento si paga in termini di potenza di calcolo richiesta per determinare soluzioni sub-ottime accurate. La prima tecnica analizzata è relativamente economica dal punto di vista computazionale e fornisce prestazioni abbastanza soddisfacenti. Tutto dipende dalla discretizzazione dei possibili valori delle variabili di ingresso: una discretizzazione fine, infatti, migliora le prestazioni dal punto di vista dell’errore, ma fa aumentare notevolmente il tempo di calcolo. Una discretizzazione grossolana, invece, permette di ridurre il tempo di calcolo ma fornisce prestazioni inferiori dal punto di vista dell’errore e delle oscillazioni di ingresso. Le procedure di ottimizzazione basate su Algoritmi Evolutivi portano a un errore sulla traiettoria piccolo, ma richiedono elevato costo computazionale rispetto alle altre, specialmente per orizzonti di controllo corti. In questa situazione si rivelano convenienti le procedure basate sulla tecnica branch-and-bound che presentano in rapporto a questi un più basso costo computazionale, ma errore più grande sulla traiettoria. Per queste procedure, però, il costo computazionale aumenta in maniera esponenziale all’allungarsi dell’orizzonte di controllo. Per orizzonti di controllo più lunghi, quindi, queste tecniche non sono consigliabili per il controllo in tempo reale.




