Un’introduzione ai concetti di base dei metodi Fast Fourier Transform per il calcolo della trasformata di Fourier discreta.
Uno degli strumenti più importanti per quanti si occupano di elaborazioni di segnali è certamente la trasformata di Fourier discreta (Discrete Fourier Transform) che consente l’analisi delle proprietà dei sistemi nel dominio della frequenza. La DFT equivale infatti al campionamento su N punti equamente spaziati sul cerchio unitario nel piano z della trasformata di Fourier di una sequenza finita di campioni. L’espressione esplicita per il calcolo della DFT di una sequenza x[n] di lunghezza N è:
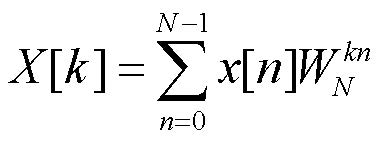
[1a]
In funzione dei coefficienti trasformati, la sequenza originaria può quindi essere ricostruita mediante l’espressione duale:
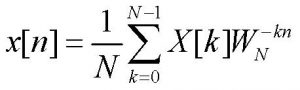
[1b]
Dalla (1) appare evidente che per il calcolo di ogni coefficiente della DFT occorrono N moltiplicazioni ed (N-1) addizioni complesse e, quindi, per l’intera sequenza trasformata rispettivamente N2 ed N(N-1) operazioni. Sfruttando le proprietà di simmetria delle funzioni di base la complessità del calcolo può ridursi di un fattore 2, risultando tuttavia ancora piuttosto elevata per la maggior parte delle applicazioni. FFT (Fast Fourier Transform) è il nome generico con il quale si indica un insieme di algoritmi piuttosto efficienti per il calcolo della DFT. Sebbene l’idea di fondo dei metodi FFT possa essere fatta risalire ai lavori di Gauss agli inizi dell’800, è solo con le pubblicazioni di Cooley e Tukey del 1965 che ne viene data una formulazione precisa. I metodi FFT si basano su una decomposizione della trasformata DFT in sotto-sequenze di lunghezza minore così da semplificare il calcolo dei coefficienti grazie anche alle proprietà di simmetria delle funzioni di base. Diverse implementazioni possono essere ottenute a seconda dei modi in cui questa decomposizione viene effettuata. Di seguito sono descritti i concetti di base di tali metodi attraverso un’introduzione agli algoritmi di decimazione in tempo ed in frequenza.
Algoritmi di decimazione in tempo
Gli algoritmi di decimazione in tempo derivano una decomposizione della trasformata a partire da una decomposizione in sotto-sequenze della sequenza originaria. Consideriamo il caso più semplice in cui N sia una potenza di 2 e decomponiamo x[n] nelle due componenti ottenute considerando, rispettivamente, i soli termini di indice pari e dispari. La (1a) può essere riscritta nel modo seguente:
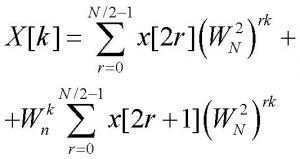
[2]
Ovvero
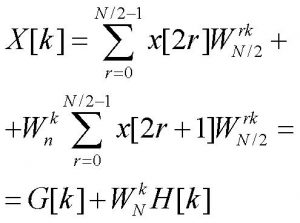
[3]
avendo usato appunto le proprietà di simmetria degli esponenziali complessi:
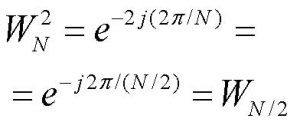
[4]
Le sequenze x[r] ed x[2r] sono funzioni periodiche di periodo N/2; G[k] ed H[k] ne rappresentano le rispettive trasformate DFT su N/2 punti. La complessità del calcolo di ognuna di tali trasformate, in base a quanto detto in precedenza, è dell’ordine di (N/2)2. Il computo della DFT mediante la (3) richiede ulteriori N moltiplicazioni ed N addizioni complesse ed ha quindi una complessità dell’ordine di N+N2/2 che per N>2 è sempre minore di quanto stimato nel caso di calcolo diretto mediante la (1a). Se N=2n, la procedura descritta può essere evidentemente iterata n volte. In figura 1a è mostrato come esempio, usando una notazione basata su grafi, il caso N=8; il grafico elementare mostrato in figura 1b viene chiamato diagramma a farfalla.
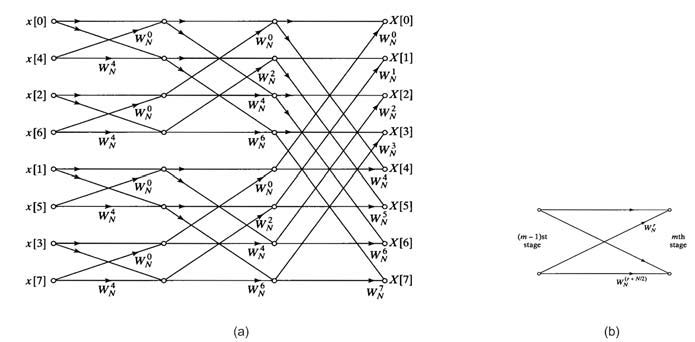
Figura 1: diagramma a farfalla per il calcolo della DFT mediante decimazione in tempo (a) caso N=8 (b) grafo elementare.
In tale grafo elementare, sono necessari per ogni coefficiente una sola moltiplicazione ed una sola addizione complessa; poiché per il calcolo della DFT occorrono Nlog2N passi, tale è pure la complessità dell’algoritmo. Rispetto al valore N della (1a), già per N=10, ad esempio, si ha una riduzione di due ordini di grandezza. Ulteriori semplificazioni possono essere ottenute sfruttando le proprietà di simmetria delle funzioni di base:
![]()
[5]
Usando queste, il grafo a farfalla della figura 1a per lo stadio m-simo può essere riscritto come mostrato in figura 2 riducendo in questo modo di un fattore 2 il numero complessivo di moltiplicazioni.
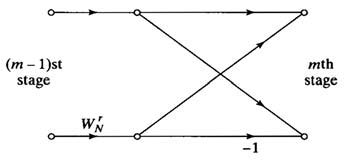
Figura 2: diagramma a farfalla semplificato.
Un aspetto interessante dei metodi di calcolo della FFT mediante decimazione in tempo è la possibilità di calcolare i coefficienti sul posto (in-place computation). Dalla figura 1 è immediato mostrare, infatti, che ogni passo della DFT trasforma un insieme di N numeri complessi in un altro insieme anch’esso di N numeri e che l’insieme di partenza non viene ulteriormente utilizzato nei calcoli successivi. Sono quindi necessari soltanto N registri (complessi) come elementi di memoria, memorizzando i risultati al posto degli ingressi al termine di ogni passo. L’unico problema è riconoscere dove memorizzare ogni termine in modo che si trovi correttamente in ingresso al successivo stadio. Analizzando sempre la figura 1, si scopre che i risultati devono essere memorizzati usando un ordinamento bit-reversed. In altri termini, se indichiamo, nel caso particolare, con (n2,n1,n0) la rappresentazione binaria della posizione p del registro Xm-1[p], il risultato dovrà essere memorizzato nella posizione (n0,n1,n2). Il motivo di questa inversione si spiega facilmente se si ripercorre il modo in cui si è giunti alla decomposizione del calcolo della DFT in grafi a farfalla. La sequenza x[n] è stata decomposta inizialmente nelle componenti di posto pari e dispari, il che equivale a discriminare in base al valore del bit n0 dell’indice di ogni campione. Ai campioni di posto pari (n0=0) sono stati associati i primi N/2 coefficienti trasformati, ovvero quelli aventi indice con bit di peso maggiore uguali a 0, mentre ai campioni di posto dispari i successivi N/2 coefficienti, ovvero quelli con indice da N/2 a N-1. Ad ogni passo e per ogni sotto-sequenza è quindi stata iterata la decomposizione in componenti di posto pari e di posto dispari, discriminando così i campioni in base al valore del bit (m-1)-simo dell’indice associato. Il grafo mostrato in figura 1 può, ovviamente, essere modificato variando la posizione dei nodi; finché la trasmittanza di ogni ramo resta la stessa, il risultato del calcolo non varia. Un’interessante variante della 1 è mostrata in figura 3, che corrisponde alla formulazione proposta da Singleton nel 1969.
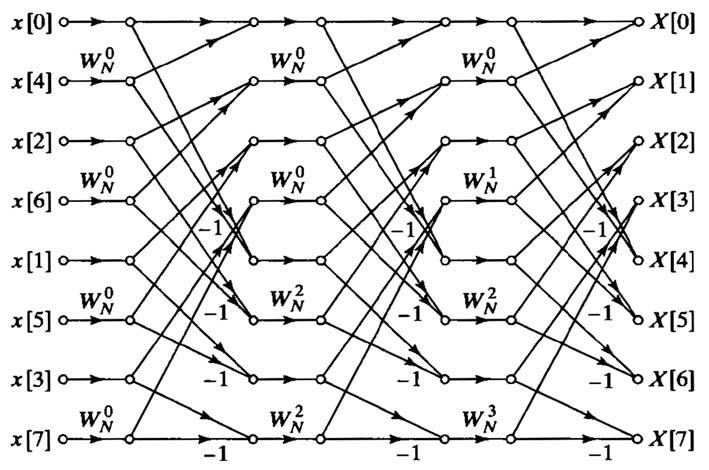
Figura 3: un metodo di decimazione in tempo con memorie ad accesso sequenziale.
Il metodo non consente il calcolo sul posto dei coefficienti ma in compenso è in grado di lavorare con memorie ad accesso sequenziale; gli algoritmi precedenti richiedono invece memorie ad accesso casuale. L’algoritmo di Cooley/Tukey descritto è il più semplice tra i metodi di calcolo della DFT mediante decimazione in tempo. Ne esistono diverse varianti (tra cui i metodi split-radix in cui la componente dispari è ulteriormente divisa nelle sequenze aventi indici con resto 1 e 3 modulo 4) come pure formulazioni alternative, che consentono di ridurre la complessità computazionale. Tra queste ultime vi sono, ad esempio: l’algoritmo Prime-Factor di Good-Thomas basato sul teorema cinese del resto ed utilizzabile nel caso in cui N sia fattorizzabile come prodotto di due numeri primi tra loro; l’algoritmo di Bruun che adotta invece una fattorizzazione polinomiale ricorsiva ma che sembra fornire minore accuratezza rispetto al metodo di Cooley/Tukey quando si tiene in conto la rappresentazione a lunghezza finita dei coefficienti; l’algoritmo di Winograd che utilizza metodi basati sul calcolo del prodotto di convoluzione nel computo delle DFT elementari in cui la trasformata è decomposta (per questo motivo non sempre viene considerato come un vero metodo FFT). Ampia documentazione è disponibile su questi metodi in bibliografia in rete; un buon punto di partenza, come spesso accade, è il sito di wikipedia.
Algoritmi di decimazione in frequenza
Se gli algoritmi di decimazione in tempo si basano, come abbiamo visto, sulla decomposizione della sequenza originaria, i metodi di decimazione in frequenza decompongono in sotto-sequenza la successione trasformata. Partiamo, come in precedenza, dalla definizione (1a) della DFT. I termini pari di tale successione possono essere espressi come segue:
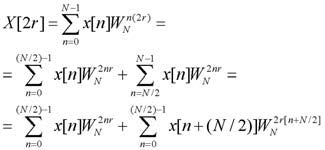
[6]
avendo operato una semplice sostituzione degli indici nella seconda sommatoria. Sfruttando le proprietà di periodicità delle funzioni di base:
![]()
[7]
e la seguente identità:
![]()
[8]
la (6) può essere riscritta come segue:
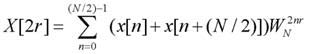
[9]
Da questa appare evidente, allora, come i termini di posto pari della successione trasformata possano essere visti come la trasformata su N/2 punti di una sequenza ottenuta sommando i termini n ed n+N/2 di quella originaria. E’ interessante osservare come tale nuova sequenza può essere considerata in realtà il risultato di un fenomeno di aliasing nel tempo, coerentemente con il fatto che deriva dalla ricostruzione in seguito a sotto-campionamento della trasformata di Fourier di x[n]. In maniera del tutto analoga a quanto esposto, possono essere calcolati i termini dispari della (1). Riportiamo di seguito per brevità solo l’espressione finale:
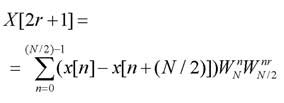
[10]
avendo sfruttato la (8) e le identità:
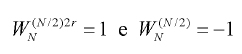
[11-12]
Anche in questo caso, sussiste un’interpretazione analoga a quella data in precedenza. I termini dispari della trasformata possono essere visti come la trasformata di una successione ottenuta da quella di partenza sottraendo i termini di posto n ed n+N/2. Come nella trattazione precedente per i metodi di decimazione in tempo, anche in questo caso si può pensare di iterare le (9) e (10) fino a ridursi al caso N=2. In figura 4 sono mostrati l’applicazione del metodo al caso N=8 ed il grafo a farfalla corrispondente al passo elementare.
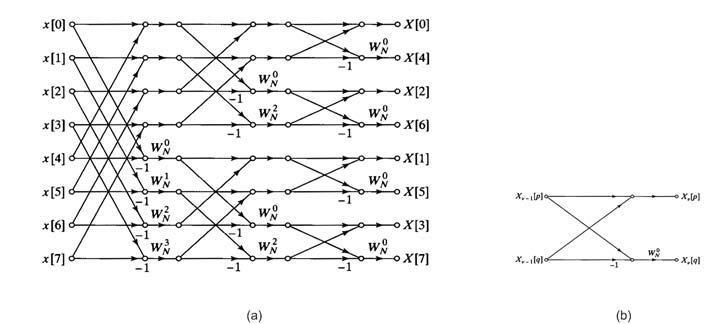
Figura 4: diagramma a farfalla per il calcolo della DFT mediante decimazione in frequenza (a) caso N=8 (b) grafo
elementare.
Da qui, generalizzando per N=2n, è immediato osservare che il numero di operazioni richieste è pari a (N/2)log2N moltiplicazioni e Nlog2N addizioni complesse come nel caso dei metodi di decimazione in tempo descritti in precedenza. Continua a valere inoltre un principio di calcolo sul posto dei coefficienti trasformati. In effetti, da questo punto di vista, è interessante osservare come i grafi nelle figure 2 e 4 siano l’uno il trasposto dell’altro. Nella teoria dei grafi, la trasposizione di un grafo si ottiene invertendo le direzione di tutti i rami nella rete mantenendo inalterati i valori di trasmittanza (ovvero i termini moltiplicativi associati ad ognuno) e trasformando nodi sorgenti in destinazioni e viceversa. Più in generale, si può dimostrare che per ogni algoritmo di calcolo della DFT mediante decimazione in tempo esiste un algoritmo equivalente basato su decimazione in frequenza che può essere ottenuto mediante semplice trasposizione del grafo del primo.






