Per quelli di noi che, prima che iniziasse una lezione all’università, si recavano compìti a depositare un modesto registratore a cassette sotto al naso del professore di turno, l’mp3 è stata una rivoluzione. Dentro una pennetta USB grande addirittura 128 Mbyte entravano anche una cinquantina di canzoni, e in breve non dovevamo più andare in giro con i pacchi di CD e il comunque ingombrante lettore portatile. Ma accanto all’evidente rivoluzione che l’mp3 ha portato nella fruizione della musica sempre, comunque e dovunque, altre più silenziose rivoluzioni hanno portato alla diffusione capillare dei cellulari. Il principio è sempre quello: prendiamo un segnale e comprimiamolo, così da poter far entrare più segnali nello stesso spazio. Siano canzoni su una chiavetta, siano segnali vocali su un canale wireless, la storia non cambia. Oggi vi presentiamo uno di questi algoritmi di compressione per segnali vocali: Speex.
DATEMI UN PO' DI BANDA
Da qualche anno a questa parte, sembra che il mondo di ingegneri e smanettoni si sia letteralmente trasformato nel Paese dei Balocchi: qualunque cosa cerchi, ti basta chiedere e la avrai. Ti serve più potenza di calcolo? Schede a basso costo? A bassissimo consumo? Sensori per misurare le cose più assurde? Hardware programmabile? Ambienti di sviluppo potenti e facili da usare? Non c’è problema. Cerca un pò su internet e troverai i "giocattoli" che fanno per te. Cerca un altro pò e troverai tutorial, guide, manuali e forum di ogni tipo per dubbi e difficoltà.
C’è però una cosa che è finita da un pezzo ed è veramente difficile procurarsene un pò: la banda. Non quella di paese, ovviamente, ma quel concetto arcano legato, per i profani, a “quanto veloce mi va internet” e, più in generale, a quanto velocemente possiamo scambiare dei dati. Siamo passati da un computer su ogni scrivania ad un computer in ogni tasca, e ogni giorno le tasche aumentano, e tutte le tasche vogliono essere collegate tra loro. Non è facile permettere lo scambio di tutti questi dati, perlomeno a velocità ragionevoli.
Gli ingegneri, come è loro natura, si sono ingegnati, e si sono resi conto che, alla fine della festa, poche sono le cose che si possono fare. Si può, ad esempio, cambiare portante, spostando i segnali da trasmettere in un range di frequenze auspicabilmente non occupato da nessuno e in cui si possa trasmettere a costi (tecnologici o energetici) tollerabili. Si può cambiare modulazione, passando, ad esempio, da un formato binario a uno M-ario, con il relativo aumento di data rate e l’associata suscettibilità al rumore, nell’ipotesi che si possano gestire gli errori in più dovuti a questa maggiore suscettibilità.
Oppure ci si può spostare più su nella pila protocollare, e lavorare direttamente sui dati da trasmettere. Se potessimo trasmettere meno dati per utente, potremmo trasmettere i dati di più utenti. Ovviamente non possiamo costringere gli utenti a trasmettere meno roba, ma possiamo fare in modo che la roba che intendono trasmettere occupi meno banda, ossia richieda meno bit al secondo per essere trasmessa. Possiamo cioè comprimere i dati, siano essi audio, video o semplice testo. Esiste un’infinità di algoritmi diversi per i vari ambiti (pensate all’mp3, al JPEG, all’mpg, al Lempel-Ziv, all’Huffman, e così via): qui vi parleremo di come sia possibile comprimere in maniera efficiente e con qualità sufficientemente buona un segnale vocale per trasmetterlo poi in real-time su un collegamento VoIP.
L’APPARATO VOCALE E' UN FILTRO LINEARE
Per quanto possa sembrare strano, è così. Siamo abituati a pensare ad un filtro come ad un oggetto che, preso in ingresso un segnale, ne restituisce un altro in uscita con diverso contenuto in frequenza, ma raramente ci preoccupiamo di che aspetto abbia il segnale nel dominio del tempo. Un segnale filtrato e ricostruito rappresenta una versione alterata in qualche modo del segnale di partenza, ma per quanto la parola “alterata” abbia un che di minaccioso, non è detto che alterare un segnale sia una cosa totalmente negativa. Chiunque abbia usato Photoshop sa che i suoi “filtri” sono strumenti che permettono di applicare un qualche effetto all’immagine che si sta “alterando”. Nel contesto dell’emissione di un segnale vocale, tutto l’apparato vocale (gola, lingua e labbra) altera le onde sonore emesse dalle corde vocali in modo da produrre una parola, e in questo senso può essere visto come un filtro.
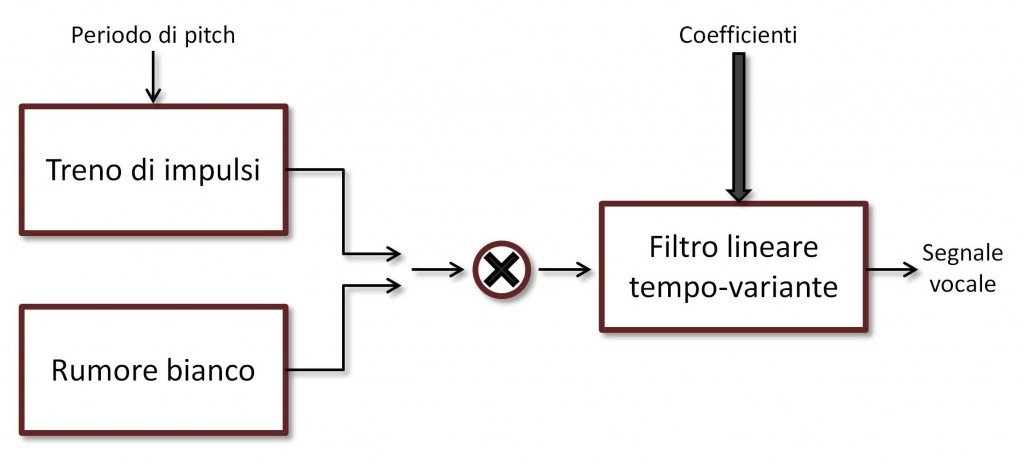
Osserviamo dunque la Figura 1. Gli impulsi sonori emessi dalle corde vocali, schematizzabili con un treno di impulsi periodico (il cui periodo viene comunemente detto “periodo di pitch”), vengono modificati dall’apparato vocale, e ciò che ne viene fuori sono le parole che ascoltiamo. Quando dalla gola risale aria senza una particolare regolarità temporale, ciò che viene prodotto dall’apparato boccale è uno di quell’ampia gamma di rumori che l’uomo è in grado di emettere. In questo caso, il segnale che entra nel filtro può essere schematizzato con un processo casuale di rumore bianco. In più, l’apparato vocale si modifica a seconda della lettera che vogliamo emettere, cambiando ad esempio la forma delle labbra o la posizione della lingua, perciò il nostro filtro è un filtro tempo-variante. Il filtro varia però lentamente, dal momento che, per le scale temporali caratteristiche dell’elaborazione digitale dei segnali (stiamo parlando di migliaia di campioni al secondo), le singole lettere vengono emesse con una certa lentezza. Su scale temporali ridotte, dunque, si può assumere che il filtro sia stazionario. Nel modello nella figura, poi, è presente anche un fattore di moltiplicazione, a ricordare il fatto che i suoni emessi non sempre avranno la stessa intensità, anche a parità di tutto il resto.
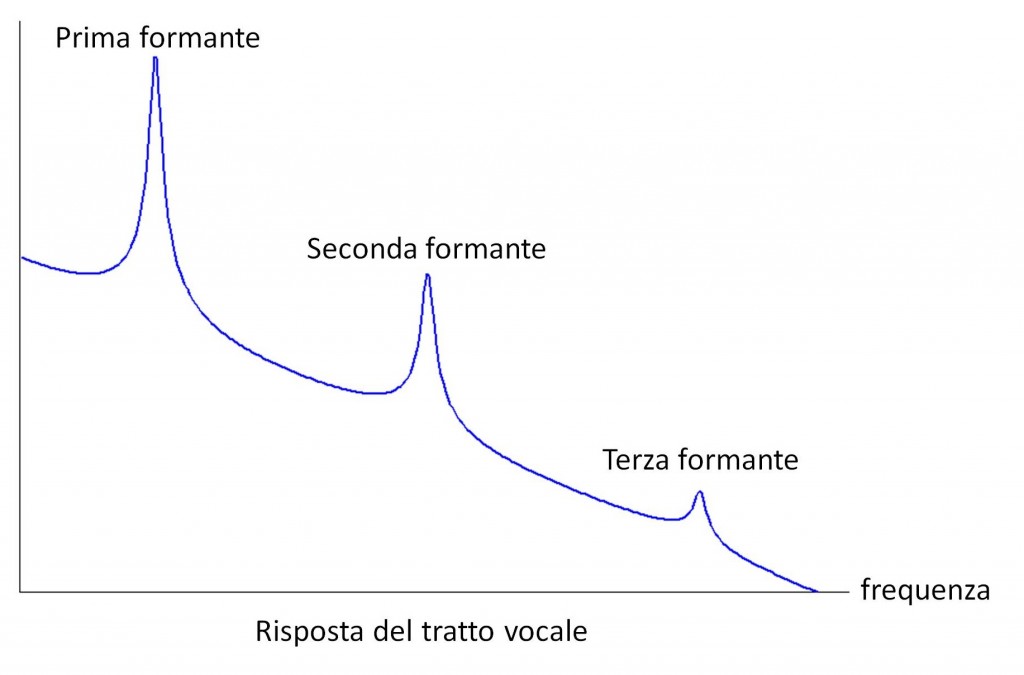
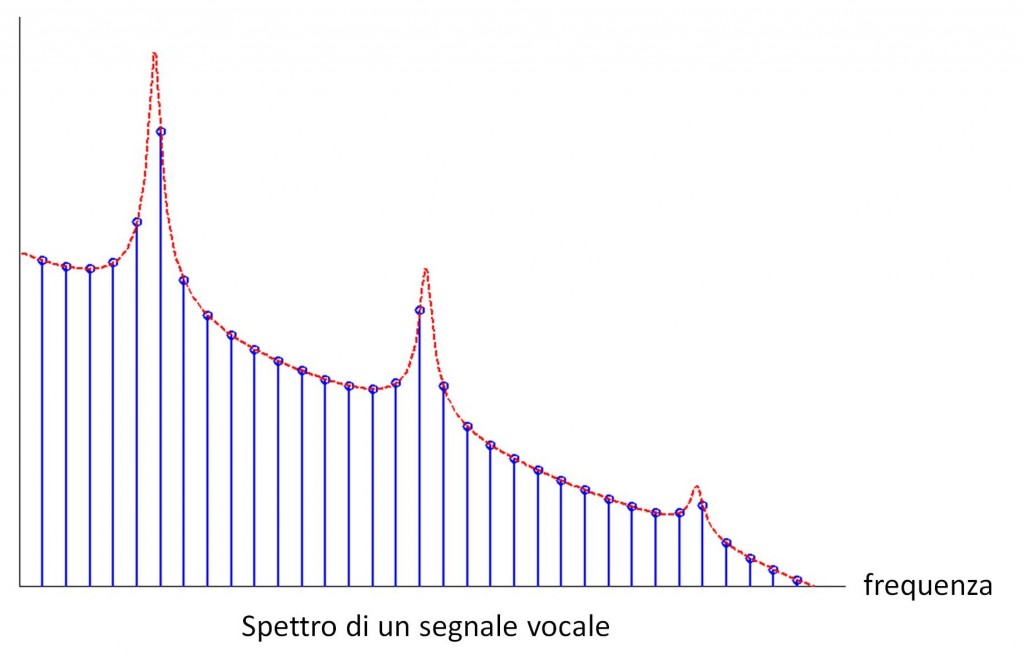
Ancora, il tratto vocale si comporta a tutti gli effetti come una cavità acustica, perciò la funzione di trasferimento del filtro sarà necessariamente di tipo risonante, con un certo numero di picchi di risonanza in corrispondenza di ben precise frequenze dette formanti, simili a quella mostrata nella Figura 1 (b). In questo modello, la risposta in frequenza del segnale vocale sarà data dal prodotto della risposta in frequenza del filtro e della trasformata di Fourier del treno di impulsi periodico, cioè un treno di delta di Dirac. Dunque, lo spettro del segnale vocale sarà simile a quello mostrato nella Figura 1 (c), ossia uno spettro il cui inviluppo rappresenta la risposta del filtro, e la cui struttura fine ricalca l’eccitazione al suo ingresso.
Molti sistemi di eliminazione del rumore si basano in misura più o meno maggiore su questo modello. Una strategia immediata consiste, ad esempio, nell’utilizzare un filtro passa-basso. L’orecchio umano non è sensibile allo stesso modo a tutte le frequenze, ma percepisce più distintamente le basse e meno le alte. L’idea dunque è che, se durante l’eliminazione del rumore in alta frequenza eliminassimo anche parte del segnale utile, probabilmente il peggioramento in termini di qualità sarebbe appena percepibile. Il problema di questo ragionamento è che molti segnali presentano contenuti considerevoli anche in alta frequenza. Se la maggior parte dello spettro associato ad un tipico segnale vocale giace al di sotto dei 4 kHz (circa), comunque la maggior parte degli strumenti musicali produce suoni con armoniche che si trovano ben al di sopra di questo limite. Una strategia di questo tipo può, ad esempio, essere usata per eliminare del rumore da una conversazione telefonica, e in questo contesto avrebbe anche l’indubbio vantaggio della semplicità e del basso costo, ma se applicata ad una canzone qualsiasi i risultati sarebbero inaccettabili.
Questa stessa tecnica si presta molto alla compressione dei segnali vocali. Pensateci un attimo: se il filtro è in grado di generare i fonemi a partire da un banale treno di impulsi, perché trasmettere i fonemi? Trasmettiamo i parametri del filtro, il periodo del treno di impulsi, il fattore di guadagno, e ricostruiamo il segnale in loco, generando un treno di impulsi dello stesso periodo e facendolo passare per un filtro con quei coefficienti. Il risparmio di banda è potenzialmente enorme, visto che ci basta trasmettere una manciata di coefficienti ogni tanto invece di ottomila campioni al secondo (supponendo di campionare il segnale vocale a 8 kHz) .
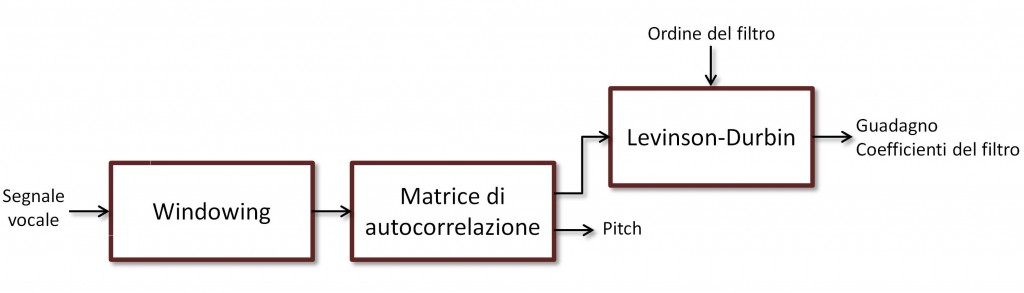
Ricavare coefficienti, guadagno e periodo di pitch non presenta particolari problemi. Esistono in letteratura una marea di algoritmi, ognuno con i suoi pro e contro, ma se volete potete accontentarvi anche del classico Levinson-Durbin per l’inversione della matrice di autocorrelazione del segnale (Figura 2). Visto che la matrice di autocorrelazione viene costruita a partire dai cosiddetti “coefficienti di predizione lineare” della risposta impulsiva del filtro, tutte le tecniche come questa vengono dette LPC, “Linear Predictive Coding”. In fin dei conti è una cosa abbastanza tranquilla. Se siete pratici di Matlab, potete buttare giù uno script per questo genere di compressione in men che non si dica. Forse la cosa più antipatica da fare è quel blocco davanti alla catena, che dice “windowing”. In effetti, non si può usare lo stesso filtro per tutto il segnale vocale, visto che, come abbiamo detto, la bocca e la lingua modificano forma e posizione a seconda di quello che vogliamo dire. Quello che dobbiamo fare è dividere il segnale in finestre sufficientemente lunghe da farci cadere dentro un fonema, ma non troppo lunghe da abbracciarne più di uno. Per ogni finestra estraiamo i nostri coefficienti, guadagno e periodo di pitch, e li trasmettiamo.
Se ancora non credete che un sistema di questo tipo possa ridurre di parecchio la banda occupata, facciamo due conti della massaia. Prendiamo un segnale campionato a 8 kHz e codifichiamolo con una PCM a 8 bit (tipico segnale telefonico): fanno 64 kbit/s. Prendiamo, invece, finestre da 20 ms, ossia 50 finestre al secondo. Per ogni finestra, immaginiamo di estrarre dieci coefficienti per il filtro, uno di guadagno e il periodo di pitch. Se avete mai progettato un filtro tempo-discreto saprete che i coefficienti tendono ad essere numeri con la virgola, per cui immaginiamo di usare numeri a 32 bit in virgola fissa; 12 numeri a 32 bit fanno 384 bit, che in 50 finestre diventano 19.2 kbit/s: più di un terzo della banda. La riduzione può essere ancora più consistente se usiamo un pò meno precisione nei coefficienti (magari 24 bit invece di 32), o se li quantizziamo in maniera più efficiente (con una quantizzazione vettoriale, ad esempio) e magari siamo disposti a tollerare una qualità leggermente inferiore.
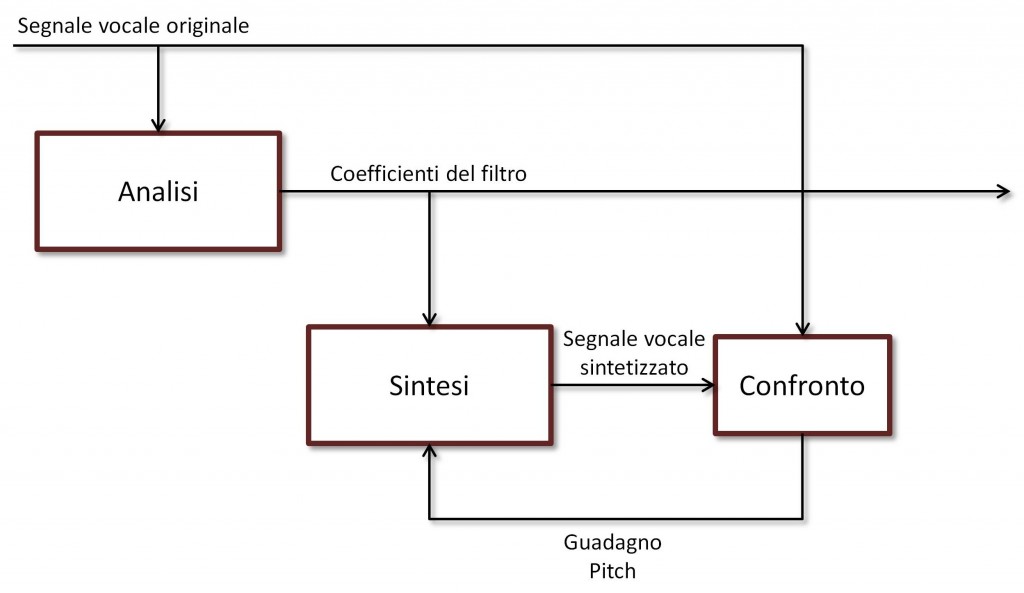
A partire da questo algoritmo di base, nel tempo sono state proposte tutte le varianti possibili e immaginabili. Una è la cosiddetta CELP (Codebook Excited Linear Prediction). Il cuore è sempre quello, ossia un LPC tramite il quale calcolare il filtro. Tuttavia, pitch e guadagno non vengono più calcolati a partire dalla matrice di autocorrelazione, ma vengono scelti da un “vocabolario” (codebook), da una memoria che contiene pitch e guadagni per i fonemi che più facilmente si possono incontrare nel parlato. Il pitch e il guadagno ottimali vengono scelti sintetizzando in loco il segnale che il filtro e il pitch scelti sono in grado di generare, e confrontandolo con il segnale originale. Si ripete l’operazione per tutti i pitch nel codebook e alla fine si sceglie quello che produce il segnale più simile all’originale.
Con il CELP ci sono un paio di seri problemi. Il primo è dato dalle dimensioni del vocabolario. Ovviamente, più sono i pitch e i guadagni, e più è facile che ne troveremo uno che dia buone prestazioni. Ma più sono i pitch e i guadagni, e più pesante sarà l’algoritmo di ricerca/confronto, oltre ad occupare più memoria. Il secondo è dato da quel “più simile all’originale”. Ovviamente, solo l’orecchio umano è in grado di dire se e quanto un segnale sintetizzato si avvicina a quello “vero”, ma non possiamo infilare un orecchio e il relativo cervello in un processore. Il massimo che possiamo fare è inventarci un qualche genere di misura che tenti di capire come giudicherebbe un certo suono un orecchio umano: in pratica, che stimi il giudizio che darebbe una persona e che scelga di conseguenza. Algoritmi di questo genere esistono, ma come potete immaginare sono piuttosto complicati, e in quanto tali pesanti computazionalmente. Se i confronti da fare sono tanti, la ricerca nel codebook potrebbe richiedere davvero tanta potenza di calcolo. [...]
ATTENZIONE: quello che hai appena letto è solo un estratto, l'Articolo Tecnico completo è composto da ben 3738 parole ed è riservato agli ABBONATI. Con l'Abbonamento avrai anche accesso a tutti gli altri Articoli Tecnici che potrai leggere in formato PDF per un anno. ABBONATI ORA, è semplice e sicuro.