
Questo articolo illustra il principio di funzionamento e i circuiti di riferimento, per la conversione della frequenza in tensione partendo dai concetti base fino all’implementazione circuitale.
Per poter comprendere l’utilità di questi convertitori, si consideri un circuito che genera un’onda quadra con duty-cicle costante e che l’unico parametro a variare sia la frequenza. In queste condizioni una variazione di temperatura produce una variazione di resistenza, quindi una variazione di frequenza. Facendo in modo che per piccole variazioni di resistenza si ottengano grandi variazioni di frequenza, si possono ottenere buone prestazioni in termini di risoluzione. In figura 1 è mostrato un semplice circuito di conversione implementato dall’integrato LM331, il circuito accetta in ingresso un treno di impulsi o un’onda quadra di ampiezza pari o superiore a 3V.
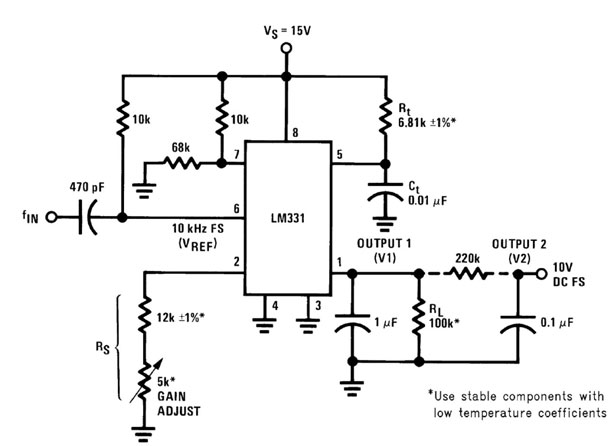
Figura 1: convertitore F/V.
La capacità di coupling di 470pF fa sì che sull’ingresso 6 si presenti un impulso negativo che porta la tensione da un valore di +15V ad un valore inferiore a +13V impostato dalla tensione di riferimento nel punto 7 del partitore resistivo. La presenza di questo impulso abilita un Flip-Flop interno che permette la carica della capacità Ct tra mite il resistore Rt. Il periodo di clock T=1.1*Rt*Ct in cui la corrente viene erogata sull’uscita del terminale 1 è pari a I1=Vref/Rs dove Rs è la resistenza totale all’ingresso 2. La tensione di uscita V1=I1*RL verrà mediata grazie alla presenza della capacità da 1uF in parallelo ad Rl. Come risultati pratici si può constatare che con un ingresso di 10kHz si ha una tensione di uscita, ai capi di Rl, pari a 10V DC. La progettazione del circuito richiede alcuni compromessi tra il ripple della tensione di uscita e il tempo di risposta del circuito. Infatti, minore è il ripple, grazie all’uso di un filtro aggiuntivo (R=220kOhm e C=0.1uF) e maggiore sarà il tempo di risposta a causa della carica del condensatore. Per ovviare a questo problema si ricorre ad un filtro attivo, figura 3 che nel caso specifico implementa un buffer di tensione con due poli: il primo è fissato dai componenti R2-C2 e il secondo dai componenti R3-C3.
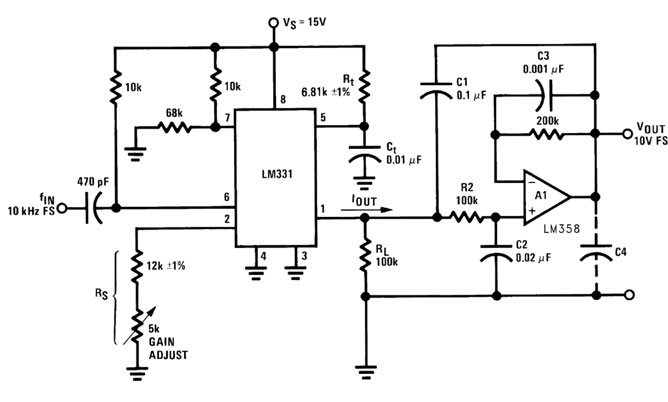
Figura 3: utilizzo di un filtro attivo con due poli in uscita.
Gli operazionali da utilizzare sono l’LM358 o l’LM324 che funzionano con singola alimentazione o, qualsiasi operazionale nel caso in cui fosse disponibile un’alimentazione negativa. Per ottenere una maggiore precisione in termini di bassa corrente di ingresso, è possibile utilizzare gli operazionali LF351B e LM308A. La funzione di trasferimento del circuito è Vo/Io=Rl/(1 + K1*ω + K2*ω2) dove K1 e K2 sono i due poli precedentemente indicati, mentre Rl è il guadagno in DC. Dalla figura 4 si possono analizzare le prestazioni delle varie tipologie di filtro andando a valutare il ripple in funzione della frequenza.
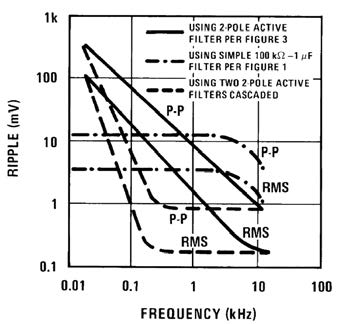
Figura 4: prestazioni dei vari filtri.
Usando un singolo polo (circuito di figura 1) si ottiene un ripple elevato ma costante in frequenza, con un doppio polo (circuito di figura 3) si ha un ripple che diminuisce linearmente in frequenza mantenendo un tempo di risposta maggiore di 30 volte rispetto al caso precedente. Per l’ultima categoria di filtri (due poli in cascata) che verranno analizzati in seguito, si avrà un ripple molto basso, costante nelle frequenze di interesse e con tempi di risposta elevati. Il filtro mostrato in figura 5 è di tipo invertente con due poli in cascata dove il filtro R5-C5 è utilizzato per ridurre l’errore in DC.
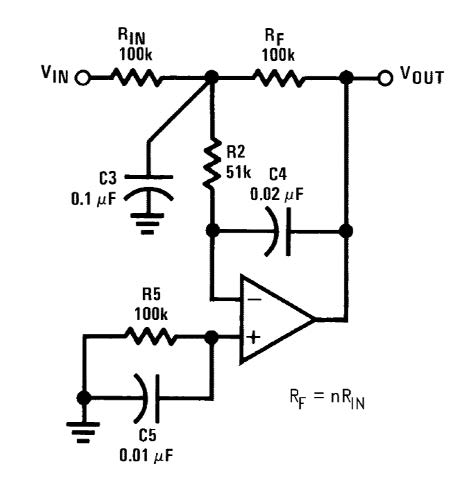
Figura 5: filtro in cascata di tipo invertente.
Da un punto di vista progettuale va scelto R5=R2+Rin//Rf, mentre la funzione di trasferimento vale:
Vo/Vin=-n/(1 + (Rf+R2+nR2)*C4*ω +Rf*R2*C3*C4*ω2) dove n è il guadagno in DC, per avere n=1, basta porre Rin=Rf.
Il circuito di figura 6 richiede, per una buona precisione, un CMRR molto elevato.
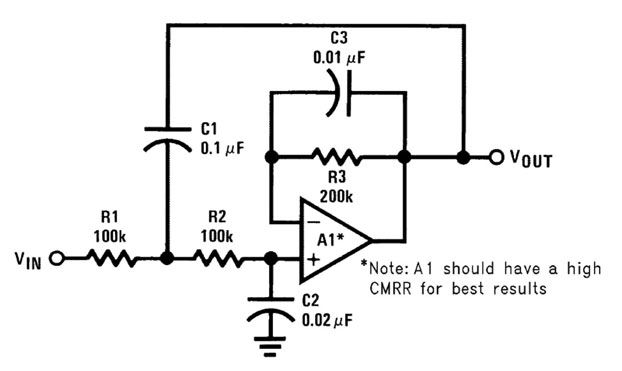
Figura 6: filtro in cascata di tipo non invertente.
Per l’integrato LM308A abbiamo un CMRR di 96dB, mentre con l’LM358B85dB. La funzione di trasferimento vale: Vo/Vin=1/(1 + (R1+R2)*C2*ω +
+R1*R2*C1*C2*ω2)
dove R3=R1+R2.
Da un punto di vista della stabilità dei componenti dalla temperatura, si può ricorrere ad alcuni accorgimenti come: l’utilizzo di un condensatore Ct in teflon o polystyrene saldato ad una temperatura non superiore a 75°C, l’utilizzo di integrati con bassa dipendenza dalla temperatura e l’inserimento di una rete di retroazione figura 7 composta da un resistore Rx di 360kOhm e due diodi 1N484.
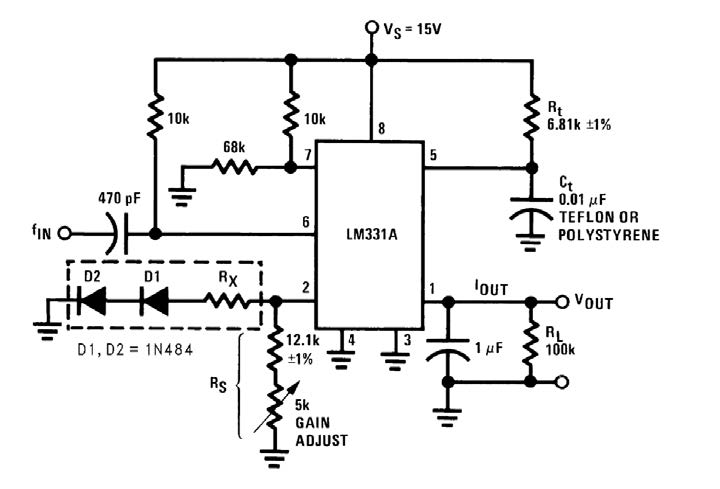
Figura 7: diodi e resistori per la riduzione del coefficiente di temperatura.





Buon giorno,
articolo molto interessante! Ho visto poche applicazioni dove viene utilizzato di questo tipo di conversione F/V o V/F. Questa conversione la trovo molto utile in applicazioni di controllo e monitoraggio remoto di un impianto con condizioni ambientali molto pesanti per problemi di interferenze EMI.
Dovendo trasmettere a distanza un segnale analogico è possibile convertirlo in frequenza ed
effettuare la conversione inversa alla ricezione, per ottenere nuovamente il segnale analogico.
Avendo a disposizione un segnale convertito in frequenza, a questo punto, è facile isolarlo galvanicamente tramite un’optoisolatore. Così da ottenere una connessione floating che consente di eliminare indesiderati loop tra le masse appartenenti a diverse apparecchiature. Prendendo in considerazione l’utilizzo di fibra ottica anzichè il rame, per realizzare i collegamenti,
si possono collegare tra loro, apparecchiature poste a differenze di potenziale di centinaia di kV. In tutta sicurezza.
Inoltre rende le connessioni totalmente immuni alle interferenze EMI.
Nelle mie specifiche applicazioni ho utilizzato l’integrato VFC32 con funzioni V/F e F/V.
Ho trovato questo integrato molto più duttile rispetto al’LM331, perchè consente con estrema facilità di cambiare tra loro le due funzioni di conversione.
Una volta calibrati i valori della costante di tempo (RC), non è più necessario cambiarli per ottenere gli stessi range di conversione tra V/F e F/V. C’è una perfetta simmetria.
Grazie.