
I microcontrollori della serie ST10 sono dotati di un coprocessore a 16 bit ottimizzato per le operazioni di elaborazione numerica e filtraggio dei segnali.
L’elaborazione numerica dei segnali trova oggi ampio utilizzo in un vasto insieme di applicazioni, che vanno dall’acquisizione dati, al progetto di regolatori industriali, al trattamento di suoni e immagini. Di particolare importanza sono quelle applicazioni che richiedono l’esecuzione in tempo reale degli algoritmi di calcolo (applicazioni real-time), come quelle del settore automotive (centraline di controllo iniezione, ABS, sospensioni…).
E’ comprensibile dunque lo sviluppo di algoritmi sempre più veloci (Fast Fourier Transform, convoluzioni, deconvoluzioni) in parallelo alla realizzazione hardware di unità di calcolo sempre più specializzate e performanti. I micro della famiglia ST10F2XX si inseriscono in quella classe di dispositivi che affiancano al la flessibilità propria dei controllori general-purpose la potenza dei DSP specializzati; essi dispongono di un coprocessore MAC 16X16 e di istruzioni di indirizzamento per la gestione dei buffers circolari dei samples di input. L’utilizzo poi del set di istruzioni Mac, realizzate specificatamente per le operazioni di convoluzione e di filtraggio e la gestione di vettori e matrici, unitamente all’efficienza del compilatore che permette di implementare istruzioni in C e Assembler, rende spesso trasparente al programmatore l’allocazione dei registri, per cui il codice diviene indipendente dal modello di memoria impiegato. Il presente articolo tratta brevemente nella prima parte alcuni principi teorici che sono alla base della realizzazione di vari tipi di filtri numerici, limitatamente al caso di strutture F.I.R.; nella seconda parte si vedrà invece l’implementazione pratica di un filtro ricorrendo alle istruzioni Mac.
Principi di filtraggio numerico
Si consideri un segnale continuo X(t), in forma complessa per poter includere l’informazione sull’ampiezza e la fase e con un’ampiezza di banda B. Si assuma che tale segnale venga filtrato con un filtro analogico le cui caratteristiche si traducono in una risposta all’impulso continua h(t) e in una risposta in frequenza H(w) (anch’essa limitata in banda). Il problema del progetto di tale filtro analogico poggia su tecniche molto progredite e collaudate, che ricorrono spesso a formule in forma chiusa relativamente semplici. Nelle applicazioni si incontra spesso il problema di trasferire il caso analogicocontinuo al caso digitale-discreto; in altri termini, dato un filtro analogico con particolari requisiti (espressi in ambito frequenziale tramite la risposta in frequenza o in ambito temporale tramite la risposta all’impulso), si presenta il bisogno di realizzare un filtro numerico che simuli il comportamento e le prestazioni del corrispondente filtro analogico. Sono due le classi di filtri numerici che rispondono a questo obiettivo: le strutture I.I.R., con risposta all’impulso infinita, e le strutture F.I.R. a risposta impulsiva finita. I pregi e i vantaggi delle due tipologie di filtri sono argomento affrontato in qualsiasi testo di elaborazione dei segnali: in prima approssimazione si può affermare che il primo tipo è di più facile implementazione, dal momento che esistono formule di progetto in forma chiusa che consentono di ricavare i coefficienti del filtro numerico partendo dai corrispondenti parametri analogici per sostituzione diretta in un certo insieme di equazioni (vedi la tecnica dell’invarianza all’impulso o quella della trasformazione bilineare). Al contrario per i filtri F.I.R. non esistono equazioni in forma chiusa, ma solo alcuni metodi iterativi che richiedono più potenza di calcolo; questi filtri offrono però l’indubbio vantaggio di avere una risposta in fase lineare e quindi l’assenza di distorsioni nel segnale estratto, oltre a prestarsi al filtraggio di segnali anche non limitati in banda (diversamente dai primi). L’articolo prenderà in considerazione il metodo delle finestre, tramite cui una risposta all’impulso infinita (derivata dalla risposta in frequenza desiderata del corrispondente filtro analogico) viene troncata in modo da ottenere un filtro numerico F.I.R. direttamente implementabile attraverso tipiche operazioni Mac.
Filtri F.I.R. tramite finestra
Uno dei metodi più immediati nel realizzare un F.I.R. (reale) partendo da un corrispondente analogico come suddetto, consiste nell’ottenere dapprima un filtro numerico ideale con risposta all’impulso infinita (e risposta in frequenza periodica) e poi troncare quest’ultima in un certo intervallo o “finestra” per realizzare il filtro digitale reale. Vediamo di formalizzare quanto espresso a parole. Indicando con Hd(ejω) la risposta in frequenza ideale desiderata del filtro numerico, ottenuta periodicizzando quella ideale analogica che chiameremo H(w) (detto in altri termini questo significa ricavare la risposta all’impulso ideale del filtro numerico tramite campionamento della risposta all’impulso del corrispondente analogico), si può scrivere:
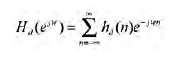
dove hd(n) è la sequenza che rappresenta la risposta impulsiva corrispondente (infinita e discreta), ovvero
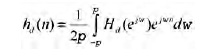
Si noti che gli estremi di integrazione coincidono con l’intervallo di periodicità della risposta in frequenza, tenendo conto che si è assunta una frequenza normalizzata w = 2πfT dove T è il periodo di campionamento della risposta h(t) da cui si ottiene hd(n). Le due uguaglianze precedenti si possono vedere come una rappresentazione mediante la serie di Fourier della risposta periodica Hd(ejω), in cui la sequenza hd(n) gioca il ruolo dei “coefficienti di Fourier”. Ricapitolando, dunque, la realizzazione del F.I.R passa attraverso la definizione di un filtro numerico ideale e poi il troncamento della risposta di quest’ultimo per avere il filtro reale. Quest’ultimo passaggio, ovvero l’approssimazione delle specifiche di un filtro ideale mediante troncamento della risposta all’impulso ideale, coincide con lo studio della convergenza delle serie di Fourier, i cui principi sono noti sin dalla metà del diciottesimo secolo. Uno dei concetti più noti di questa teoria riguarda proprio il problema della convergenza non uniforme della serie, legata al fenomeno di Gibbs. Vediamo cosa comporta troncare una risposta all’impulso infinita con una finestra. Se hd(n) ha durata infinita, un modo di ottenere una risposta all’impulso di durata finita hr(n) (fisicamente realizzabile) è il seguente:
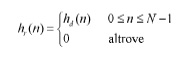
In generale, hr(n) può essere rappresentata come il prodotto della risposta desiderata e di una “finestra” w(n) di durata finita, ovvero hr(n)=hd(n)w(n). La finestra è stata scelta in modo che la risposta troncata sia nulla per tutti gli istanti minori di zero, in modo da avere un filtro causale.
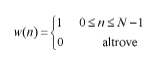
Di conseguenza il teorema della convoluzione dice che
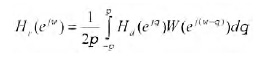
ovvero la risposta in frequenza reale, Hr, è la convoluzione continua periodica della risposta in frequenza voluta Hd con la trasformata di Fourier della finestra. Di conseguenza la risposta in frequenza del F.I.R. reale che otterremo sarà solo una versione “smussata” della risposta ideale: saranno inevitabili delle distorsioni in ampiezza nel segnale riprodotto (figura 1).
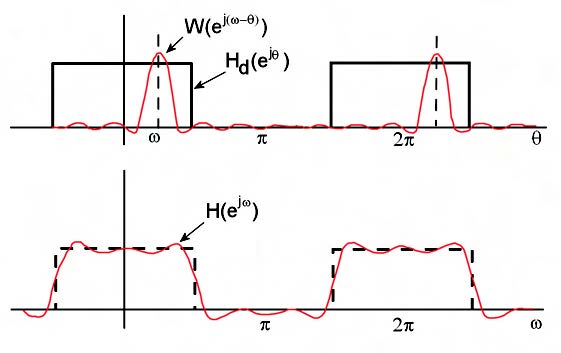
Figura 1: operazione di convoluzione corrispondente al troncamento della risposta all’impulso e risposta approssimata corrispondente all’applicazione della finestra.
Dalla figura 1 si vede che se la W è a banda stretta rispetto alle variazioni di Hd, allora la risposta reale ottenuta “assomiglierà” di più a quella ideale. Perciò i criteri di scelta della finestra sono, da una parte avere w(n) la più corta possibile in quanto a durata per ridurre la complessità dei calcoli negli algoritmi di filtraggio, e dall’altro, quella di avere la trasformata di questa finestra la più stretta possibile in frequenza, in modo da riprodurre il più possibile fedelmente la risposta desiderata. Questo perché la trasformata W di una finestra rettangolare è di questo tipo, cioè a parte un contributo di fase lineare è espressa da una funzione sinc().
Come si può vedere dalla figura 2 quando N aumenta, e quindi quando aumenta la larghezza della finestra di campionamento, i lobi principali della funzione sinc() diminuiscono di larghezza; così fanno anche i lobi secondari, ma entrambi aumentano d’altezza in modo da conservare la superficie sottesa.
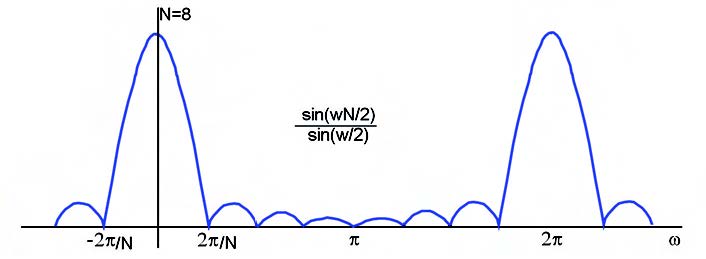
Figura 2: andamento del modulo della funzione sinc().
Il risultato di questo fatto è che quando W nell’integrale di convoluzione, incontra una discontinuità di Hd (come nelle transizioni di banda), l’integrale varia in modo oscillatorio mentre i singoli lobi della funzione sinc() si sovrappongono alla discontinuità. Anche aumentando N pertanto, restando costante l’area sotto i lobi, le oscillazioni aumentano di frequenza ma non diminuiscono in ampiezza; per ridurre quest’ultima si usano altri tipi di finestre (Hanning, Blackman, Bartlett) che realizzano un troncamento meno brusco della serie di Fourier, ovvero una transizione meno ripida in corrispondenza della discontinuità. La tabella 1 mostra in alto a sinistra la risposta in frequenza di un tipico passa-basso; a destra la risposta impulsiva ideale analogica (continua) e digitale (campionata).
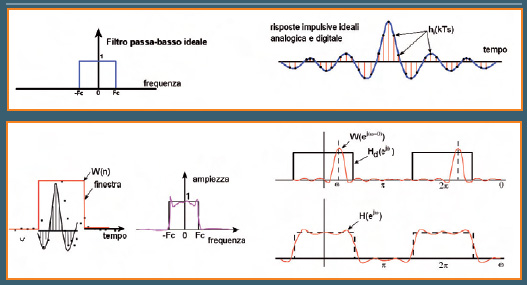
TABELLA 1: risposta in frequenza di un tipico passa-basso
In basso è riportato il disegno della finestra di campionamento della risposta ideale e a fianco gli andamenti periodici delle risposte in frequenza ideale e reale: sono evidenti le oscillazioni dovute al fenomeno di Gibbs. I passi che vanno seguiti nel progetto di un F.I.R. sono dunque: il campionamento di una risposta impulsiva ideale con una frequenza sufficientemente elevata da non creare aliasing nel segnale ricostruito e un successivo troncamento dei campioni, realizzato in modo da ottenere un filtro numerico reale e causale. Una volta ottenuti i campioni nella finestra scelta, questi diverranno i coefficienti del filtro. L’uscita di quest’ultimo a ingressi generici sarà poi data dalla convoluzione discreta tra ingresso e coefficienti e il relativo calcolo sarà eseguito come un’operazione Mac. Vediamo alcuni esempi. Nel caso di un passa basso come quello riportato in tabella la risposta impulsiva ideale analogica sarà una funzione sinc(); la risposta ideale del filtro numerico corrispondente sarà data dal campionamento di tale funzione, con una frequenza tale da rispettare la condizione di Nyquist. A questo punto abbiamo ancora un filtro non-causale: considerando solo i campioni corrispondenti ad istanti positivi e, troncandoli con una finestra come suddetto, si realizza un F.I.R. reale, con una risposta che assomiglia a quella ideale voluta pur con le limitazioni viste. Così i coefficienti del passa-basso numerico di ordine N (dove il grado coincide col numero dei campioni considerati) saranno dati da:
![]()
in cui Fc è la frequenza di cut-off e Fs quella di campionamento della risposta impulsiva ideale. Nella formula hr(n) assume valori diversi da zero per n compreso tra 0 e N-1 e nulli al di fuori di questo intervallo (figura 3).
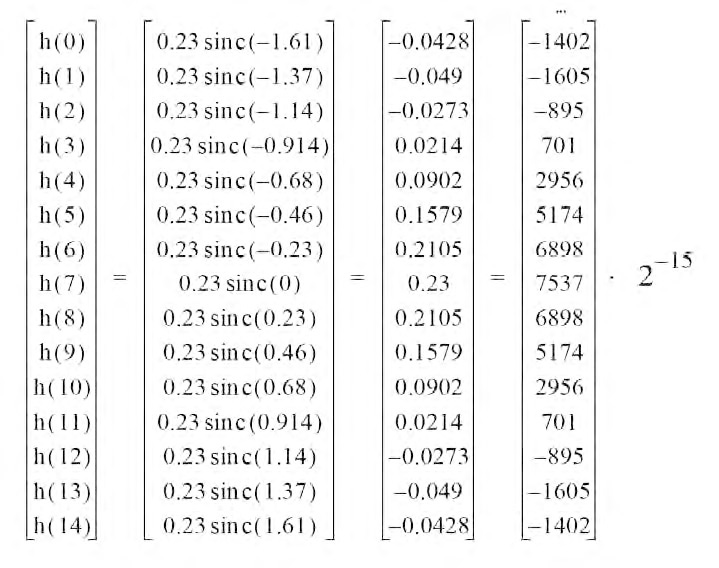
Figura 3: coefficienti F.I.R. ricavati dalla funzione sinc().
La tabella 2 mostra la relazione tra alcuni tipi di filtri e i coefficienti del F.I.R. corrispondenti.
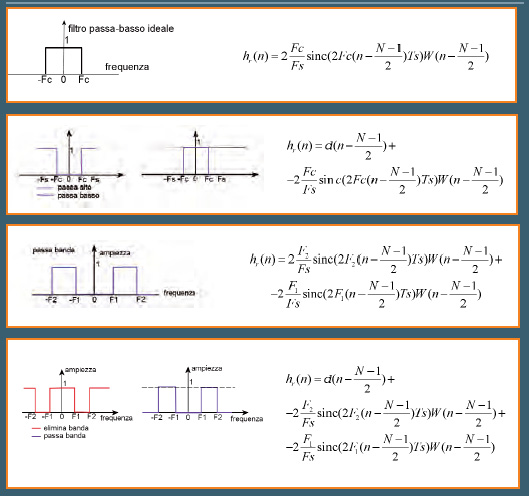
TABELLA 2: relazioni di alcuni filtri
Implementazione del F.I.R. con operazioni MAC
La figura 4 riporta lo schema tipico di implementazione del F.I.R. tramite un ST10.
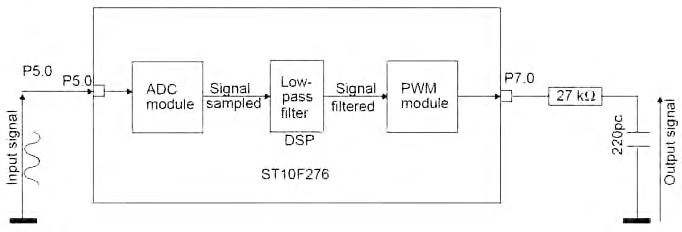
Figura 4: schema a blocchi di implementazione del F.I.R..
L’esempio si riferisce ad un filtro passabasso con una frequenza di cut-off di 2 KHz e un ordine N di 14. I vari passi di cui si compone il set-up del micro consistono in:
1- Inizializzazione del modulo PWM: questo, col filtro RC, realizza il DAC che ricostruisce il segnale filtrato. I registri del modulo devono essere settati in modo da avere una frequenza generata di 158 kHz; la cella RC ha un cut-off di 26 kHz e permette di rimuovere la componente ad alta frequenza del PWM. Il sample in uscita dal DSP viene utilizzato per impostare direttamente la larghezza d’impulso del segnale PWM.
2- Inizializzazione della struttura che realizza il F.I.R. (vedi paragrafo successivo): questa trasforma il sample di input X(n) nel sample d’uscita Y(n) tramite la convoluzione Y(n) = X(n) x Hr(n) (dove Hr(n) sono i coefficienti del filtro, ovvero i campioni della risposta impulsiva visti nel paragrafo precedente). Tutti i calcoli sono eseguiti in aritmetica intera, coi valori di input, output e i coefficienti salvati nel formato Q1.15, ovvero nell’intervallo [-1,1[ con segno. I valori forniti dal DAC, a 10 bit, vanno normalizzati in questo formato, a16 bit, mediante shift a sinistra.
3- Inizializzazione dell’ ADC e del buffer circolare d’ingresso (vedi paragrafo successivo). Quando la conversione è finita il valore memorizzato nel registro ADDAT (X(n)) viene passato alla routine che realizza il F.I.R. (vedi diagramma in figura 5).
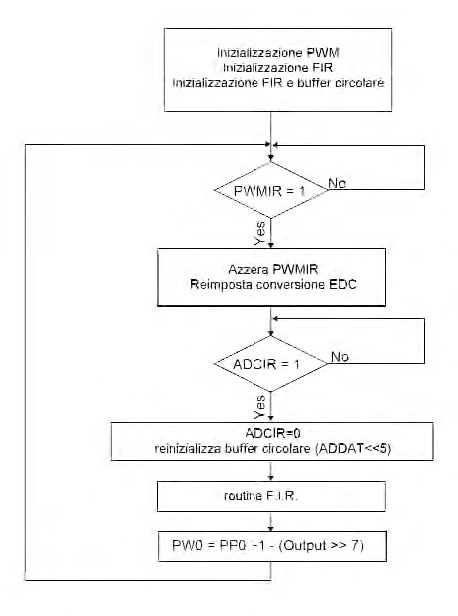
Figura 5: schema a blocchi del firmware.
Si noti come i valori in ingresso dall’ADC e quelli per il PWM devono essere normalizzati mediante shift a sinistra (ADDAT <<5) e a destra (Output >>7).
Operazione di convoluzione
Si esamina in questo paragrafo l’operazione di convoluzione che implementa la struttura FIR. X(n) è il sample di input (16 bit), h(k) il kesimo coefficiente del filtro (32bit) e Y(n) il sample d’uscita (16bit). In pseudo-codice l’operazione di convoluzione tra l’ingresso e la risposta all’impulso è la seguente:
y(n)=0;
for (k=0 to L-1) {y(n) = y(n) + h(k)*x(n-k)}
La figura 6 illustra la mappa di memoria del DSP: IDX0 contiene l’indirizzo del sample di input x(n-L+1), R9 contiene l’indirizzo della parte bassa del coefficiente Hl(L-1), R10 l’indirizzo della parte alta dello stesso coefficiente (il coefficiente è a doppia precisione).
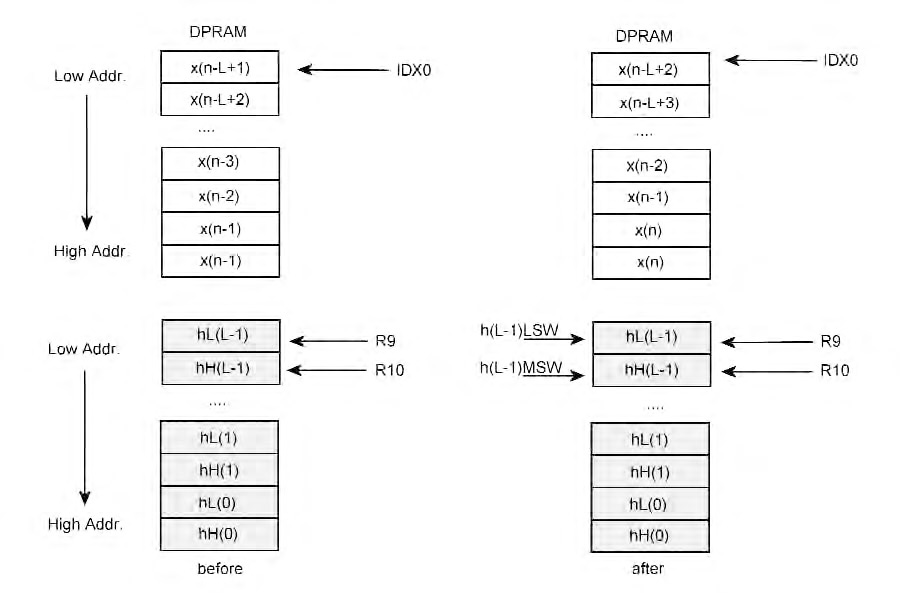
Figura 6: mappa di memoria con input e coefficienti del F.I.R. prima e dopo un’operazione CoMul.
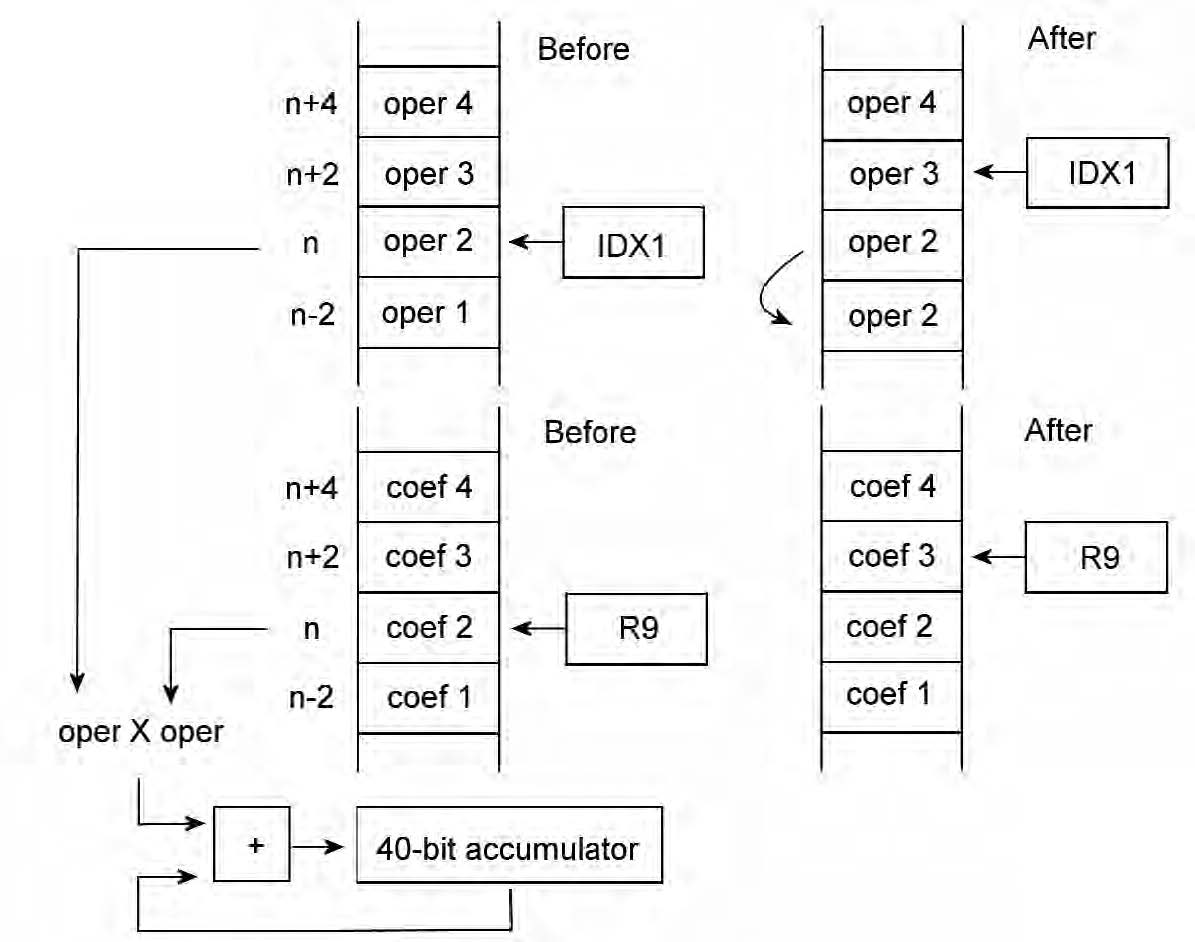
Figura7 : mappa della memoria del micro prima e dopo
un’operazione CoMACM.
Durante la routine di calcolo, ad ogni moltiplicazione (ad ogni incremento di K) l’indirizzo IDX0 viene incrementato di 2 byte (perché i sample di input sono words), mentre R9 ed R10 vengono incrementati di 4 byte poiché i coefficienti sono a 32 bit. La routine moltiplica prima tutte le parti basse dei coefficienti con i sample di input, li somma e poi fa la stessa operazione con le parti alte; alla fine somma insieme i risultati a produrre il sample d’uscita. Le costanti che compaiono nella routine sono:
R0 = 0000h, QX0 = 2*(L-1), QR0 = 4, QR1 = 4*(L-1), MRW è un contatore di ciclo caricato in modo da eseguire tutte le moltiplicazioni. L’operazione CoMUL è propria del coprocessore matematico e oltre ad eseguire la moltiplicazione, incrementa simultaneamente gli indirizzi degli operandi (vedi Listato 1).
Mov mrw #L-4 //inizializzazione del contatore//
Mov @x(n) ADC_sfr //nuovo sample di input//
CoMULsu [IDX0+] [R9+QR0] //moltiplica hl(l-1)*x(n-L+1) e incrementa gli indirizzi di IDX0 di 2 e R9 di 4//
(da ripetere mrw volte) CoMACsu [IDX0+] [R9+QR0] (operazione di MAC)
CoMACsu [IDX0-QX0] [R9-QR1] //ultima moltiplicazione;ripristino degli indirizzi iniziali del buffer circolare//
Mov mrw #L-4 //si salvano solo i 16 bit più significativi dell’accumulatore, aggiungendo solo
l’eventuale resto di quelli meno significativi e si ripete il ciclo
delle moltiplicazioni e delle somme con i bit più significativi dei coefficienti del filtro//
CoRND
CoASHR 8
CoASHR 8
CoMAC [IDX0+] [R9+QR0]
(da ripetere mrw volte) CoMACM [IDX0+] [R10+QR0] //questa operazione è simile alla CoMACsu,
ma incrementa anche l’indirizzo di x(n-i),
in modo da far posto al nuovo sample di input.//
CoMACM [IDX0-QX0] [R10-QR1]
Nop //operazione necessaria perché non c’è sincronismo tra l’unità DSP che si è usata finora
e la CPU che esegue il Mov successivo//
Mov DAC_sfr MAH //invia i 16 bit più significativi dell’accumulatore,
che contengono il sample d’uscita y(n) al DAC//
| Listato 1 |





A proposito di segnali vi segnalo questo link https://it.emcelettronica.com/portento-della-matematica-trasformata-di-fourier 😉