Filtri PLL per rfPIC

I dispositivi microchip delle famiglie RFPIC e RFHCS sono dotati di un trasmettitore RF integrato in grado di operare su diverse bande di frequenza a seconda della versione. Questi dispositivi possono trasmettere dati con una veloità massima di 40 Kbps, utilizzando una modulazione ASK o FSK della portante RF generata tramite un PLL. Ecco come calcolare i componenti di un filtro PLL, in modo di garantire le proprietà di stabilità dell'oscillatore e la qualità dell'emissione RF.

Il PLL degli rfPIC/rfHCS

In figura 1 è raffigurato lo schema a blocchi del PLL degli rfPIC. Nel seguito supporremo di usare una frequenza di trasmissione pari a 433.92 MHz, tipica dei dispositivi operanti nella banda permessa per i sistemi di controllo e sicurezza.

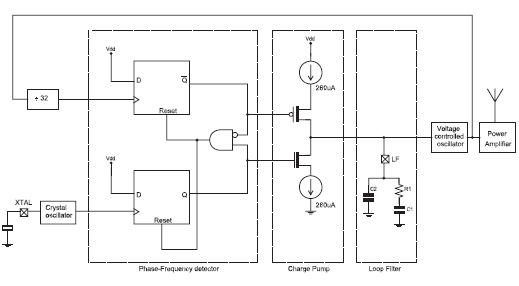
Figura 1: schema a blocchi del PLL degli rfPIC/rfHCS.

L’oscillatore a quarzo genera la frequenza di riferimento di 13.56 MHz, mentre il VCO genera la frequenza di trasmissione. Tale frequenza viene divisa per 32 e riportata ad uno degli ingressi del comparatore di fase-frequenza per essere confrontata con la frequenza di riferimento. Se il segnale generato dal VCO è in ritardo rispetto al segnale di riferimento, la pompa di carica fornisce un impulso di corrente che carica il condensatore C2, aumentando così la tensione di pilotaggio del VCO per riportare la sua uscita in fase. Al contrario se il segnale del VCO è in anticipo, C2 viene scaricato dalla pompa di carica diminuendo così la tensione del VCO. Si noti che la frequenza di riferimento corrisponde alla frequenza massima con la quale il segnale generato dal VCO può essere corretto. Lo scopo del filtro consiste, oltre che nel generare la tensione di controllo del VCO, nel controllare la larghezza di banda del loop, come vedremo più avanti. Un PLL è un esempio di sistema di controllo ad anello chiuso: secondo la teoria del controllo viene descritto tramite la sua funzione di trasferimento W(s) nel dominio della variabile complessa s:

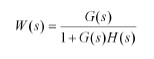
dove G(s) è la funzione di trasferimento della catena diretta, mentre G(s)H(s) è la funzione di trasferimento ad anello aperto (open loop). La funzione G(s)H(s) determina le caratteristiche di precisione e stabilità del sistema. Nel nostro caso specifico avremo che:

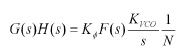
dove K_Φ rappresenta il guadagno del comparatore di fase-frequenza, espresso in A/rad, F(s) è la funzione di trasferimento del filtro, K_VCO è il guadagno del VCO espresso in (rad/s)/V. La costante N è il rapporto di divisione ed il fattore 1/N corrisponde ad H(s). Tutte queste grandezze sono note, tranne la F(s) che è proprio ciò che dobbiamo determinare. Notiamo che il termine K_VCO è diviso per s: la divisione per s infatti corrisponde alla trasformata di Laplace della integrazione nel tempo. Questa operazione è necessaria per ottenere la grandezza fase (che viene confrontata con la fase di riferimento) a partire dalla frequenza in uscita dal VCO.
Deriviamo la F(s) considerando che la rete è costituita dal parallelo di C1 e del gruppo R1-C2, ed evidenziando gli zeri ed i poli:

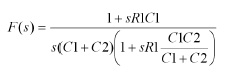
F(s) presenta quindi uno zero la cui costante di tempo è

un polo in zero ed un altro polo con costante di tempo

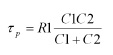
La funzione di trasferimento ad anello aperto diventa, sostituendo la F(s):

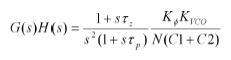
Il PLL degli rfPIC risulta essere quindi del tipo II, in quanto il comparatore permette l’aggancio sia in frequenza che in fase: da ciò deriva il polo in zero del 2° ordine. La sintesi di un sistema di controllo può essere effettuata considerando la risposta armonica ad anello aperto, ricavata sostituendo jω alla variabile s nell’equazione precedente, ottenendo così l’equazione seguente [eq. 1]:

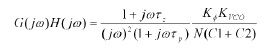
Vedremo nel prossimo paragrafo come determinare i valori dei componenti in funzione di alcune caratteristiche prefissate che vogliamo ottenere dal sistema.

Requisiti da ottenere con il filtro PLL

Vediamo quali sono i requisiti di base che vogliamo ottenere dalla progettazione del filtro. La trattazione che segue è basata sull’application note AN846 di Microchip, scaricabile dal sito www.microchip.com.

Larghezza di banda e rumore di fase

Una delle caratteristiche più importanti dei PLL è il rumore di fase (phase noise): questo comporta un’emissione di rumore intor no alla frequenza nominale del VCO. Il filtro diminuisce tale rumore all’interno della larghezza di banda. All’aumentare della larghezza di banda tuttavia, aumenta l’emissione di rumore dovuto al comparatore: questo compare sotto forma di spurie in corrispondenza della frequenza portante più o meno i multipli in teri della frequenza di riferimento (nel nostro caso di 13.56 MHz). Un compromesso tra queste due esigenze di mantenere il rumore di fase basso e controllare l’emissione di spurie, viene raggiunto con una larghezza di banda di circa 1 MHz. Ancora, una larghezza di banda di 1 MHz risulta un buon compromesso considerato che la modulazione FSK negli rfPIC viene ottenuta forzando l’oscillatore di riferimento ad una frequenza diversa da quella nominale del quarzo, e ciò limita di per sé il data rate.

Il calcolo dei componenti del filtro

I componenti del filtro R1, C1 e C2 vengono calcolati con l’ausilio di un foglio elettronico Excel. A causa di alcune imprecisioni nell’esposizione fatta nell’AN846 e per maggiore chiarezza, ritengo opportuno specificare nel seguito come vengono derivate le formule per il calcolo. Il margine di fase (vedi riquadro alla pagina seguente) è la differenza tra 180° (π radianti) ed il ritardo di fase della risposta armonica ad anello aperto (Eq. 1), alla frequenza per la quale il guadagno della stessa è pari ad 1. Il margine di fase viene fornito dal polo e dallo zero corrispondenti rispettivamente a τ_p e τ_z [eq.2]:

Il nostro scopo è quello di imporre un certo margine di fase m_Ø ed una data larghezza di banda, collegata alla pulsazione di transizione del filtro ω_t. Poichè l’Eq.2 ha il massimo per

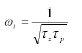
cioè per

sostituendo ω_ττ_z con la precedente nella Eq.2, imponiamo che l’anticipo di fase max sia raggiunto in corrispondenza della ω_τ voluta. Risolvendo per τ_p otteniamo infine [eq.3]

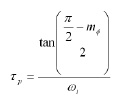
mentre sarà [eq.4]

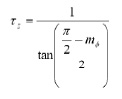
Possiamo ora determinare i valori dei componenti R1, C1 e C2 utilizzando valori che abbiamo derivato per τ_p e τ_z. Dalla risposta ad anello aperto (Eq. 1), imponendo che il guadagno sia pari ad 1 alla pulsazione ω_t, otteniamo che [eq.5]

Ricaviamo allora i valori di C1 e C2:

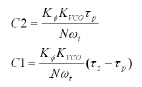
Infine ci dà il valore di R1

Uso dello spreadsheet per il calcolo del filtro

Come detto, il calcolo dei componenti del filtro è semplificato dall’uso del foglio elettronico di Excel, visibile in figura 2.

Figura 2: lo spreadsheet con i valori dell’esempio di calcolo del filtro PLL.

Lo spreadsheet è suddiviso in tre settori corrispondenti alle fasi di sintesi ed analisi del filtro. Nel primo settore vengono immessi i requisiti richiesti dal nostro sistema: frequenza del VCO, larghezza di banda e margine di fase desiderati. Si noti che K_VCO varia leggermente al variare della frequenza nominale del VCO: lo spreadsheet ricava K_VCO interpolando i valori di una tabella di look-up incorporata. Quindi vengono calcolati i valori delle costanti di tempo e da queste i componenti del filtro R1, C1 e C2, utilizzando le formule che abbiamo derivato in precedenza. Notiamo che c’è un errore nel calcolo della ω_n del filtro nello spreadsheet, che comunque non pregiudica i calcoli successivi. Nel secondo settore è possibile sostituire i valori calcolati con i valori normalizzati più vicini: vengono quindi ricalcolate le prestazioni del filtro considerando anche le tolleranze dei componenti. Nel terzo settore dello spreadsheet, vengono immessi i risultati di alcune misure sperimentali per verificare se il margine di fase e la larghezza di banda ottenute si avvicinano a quelle volute. Le tolleranze dei componenti attivi e passivi e le capacità parassite chiaramente influenzano le prestazioni ottenute.

L’analisi del transitorio

L’analisi della risposta al transitorio viene effettuata rilevando con un oscilloscopio il segnale sul pin LF del dispositivo e procedendo nel modo seguente: ponendo a livello logico alto il pin RFEN si abilita l’oscillatore a quarzo di riferimento ed il VCO. A causa della differenza iniziale di fase tra i due oscillatori, la pompa di carica emette una serie di impulsi che caricano velocemente i condensatori C1 e C2 facendo aumentare il livello sul pin LF. Quando il PLL è agganciato il livello sul pin LF raggiunge un livello pressocchè costante che è quello necessario per mantenere il VCO sulla frequenza voluta. Analizzando questo transitorio possiamo derivare il margine di fase ottenuto tramite il filtro, misurando le tensioni di picco, finale e di minimo (dopo il picco). Il margine di fase viene in realtà calcolato in base al fattore di smorzamento ζ derivato dalle misure suddette e utilizzando quindi la formula seguente (indichiamo il margine di fase in gradi anziché radianti) [eq.6].

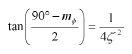
Per i più curiosi, l’Eq. 6 è ricavata dall’equazione caratteristica della W(s) (è il denominatore della W(s) ), da cui risulta, dalla definizione di ζ [eq.7]:

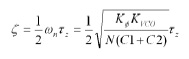
Utilizzando l’Eq. 5 per ricavare ω _t e confrontandola con l’Eq. 7 otteniamo [eq.8]:

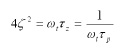
e finalmente, sostituendola nell’equazione che ci dà τ_p (Eq. 3) otteniamo l’Eq. 6. Il legame tra le misure di tensione effettuate ed il fattore di smorzamento ζ, può essere invece ricavato dall’antitrasformata di Laplace della risposta al gradino della W(s), cioè da

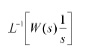
Risparmiamoci pure il calcolo e facciamo riferimento alle formule usate nello spreadsheet per ulteriori chiarimenti. Notiamo che il valore verificato del margine di fase risulta essere di 33°, di molto inferiore ai 50° voluti: questo deriva da un fattore di smorzamento ζ pari a 0.68, mentre quello calcolato, ricavabile dall’Eq. 8, è pari a circa 0.83. Volendo possiamo anche ricavare la pulsazione naturale ω_n immettendo il tempo che intercorre tra il punto di picco ed il minimo.