Chiunque utilizzi sensori o trasduttori di diverso genere ha senz’altro verificato quanto la loro precisione venga condizionata dalle variazioni termiche; ha anche constatato come la deriva, ben lontana dall’essere una funzione lineare della temperatura, sia alquanto difficile da compensare. Ancora una volta i microcontrollori possono dimostrarsi degli alleati preziosi nel risolvere il problema.
In questo articolo vedremo come, in particolari condizioni, il fattore temperatura possa condizionare l’accuratezza dei sensori elettronici, di conseguenza elaboreremo una strategia di compensazione a queste eventuali derive nelle misure, utilizzando un software di calcolo per interpolare la curva di caratterizzazione del sensore e un microcontrollore per la compensazione in tempo reale delle misure. In particolare, prenderemo in considerazione i sensori di temperatura descrivendo brevemente il loro funzionamento, per poi vedere, tramite un esempio pratico, come compensare le incertezze sulle misure tramite un generico microcontrollore. Ovviamente la tecnica di compensazione che andremo a sviluppare si potrebbe applicare ad un qualsiasi sensore che abbia una curva di caratterizzazione non lineare.
FUNZIONAMENTO DEL SENSORE
I sensori di temperatura generalmente utilizzano un transistor PNP in saturazione per la misura della temperatura ambiente. Generalmente, infatti, i transistor non sono altro che due diodi con un terminale comune (la base), la tensione delle due giunzioni che costituiscono il transistor, ed in particolare quella tra la base e l’emettitore, è funzione della temperatura, quindi conoscendo tutti i parametri presenti nell’espressione della tensione di giunzione, si ricava la temperatura alla quale si trova il transistor. Partendo dall’espressione della tensione di giunzione:
vf = (kTA/q)ln(IF/IS), IF>>IS
dove:
k = 1.3807 x 10-23 J/K = Costante di Boltzmann
q = 1.6020 x 10-19 Coulomb = Carica dell’Elettrone
TA = Temperatura Ambiente
IF = Corrente Diretta
IS = Corrente di Saturazione
e considerando che le correnti che appaiono nell’espressione sono entrambe costanti ed in particolare IS dipende dalla grandezza del transistor, mentre IF è la corrente di bias del diodo, la temperatura ambiente è l’unica incognita dell’espressione, quindi, una volta misurata la tensione di giunzione, la temperatura viene facilmente ricavata. Per ottenere una misura più precisa, spesso vengono utilizzati due transistor, infatti, la corrente di saturazione del transistor, oltre a dipendere dalle dimensioni di quest’ultimo, spesso dipende anche dalla temperatura in cui si trova. L’introduzione di un secondo transistor, quindi, permette la creazione di un match tra le due correnti presenti nei due transistor con la conseguente eliminazione della corrente di saturazione nell’espressione della tensione di giunzione. Infatti, considerando due giunzioni con due correnti dirette diverse (IF1, IF2 ) e tali che (IF2/IF1) = N si definisce la “tensione proporzionale alla temperatura assoluta” V PTAT come VPTAT = ΔVF = VF1-VF2.
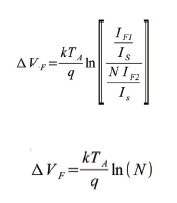
Quindi, con due transistor la misura della temperatura diventa funzione del rapporto tra le due correnti sulle due giunzioni, è importante avere una buona misura di quest’ultimo in quanto un piccolo errore di misura sulla stima del rapporto potrebbe causare errori non trascurabili nel calcolo della temperatura.
INTERPOLAZIONE DELLA CURVA D’ACCURATEZZA DEL SENSORE
In matematica per interpolazione si intende un metodo per il calcolo di una funzione y = f(x), dati una serie di valori per x ed y, ovvero partendo da un insieme di punti (x,y) ottenuti da misure sperimentali o da campionamenti, l’interpolazione permette di ricavare la funzione o la famiglia di funzioni che passano per questi punti, o nelle loro vicinanze (curve di fitting). In questa sede trascureremo le procedure matematiche che portano al calcolo delle varie curve di fitting ed interpoleremo la curva d’accuratezza del sensore utilizzando un programma di calcolo numerico, ovvero Scilab. Scilab è un programma di computazione numerica, è liberamente basato sul linguaggio di programmazione C, ed è molto simile nelle sue funzionalità al ben più noto MATLAB, il programma è totalmente gratuito ed è possibile scaricarlo direttamente dal proprio sito (http://www.scilab.org/). All’apertura, il programma dà subito accesso alla console, in cui l’utente può facilmente scrivere i comandi da dare al calcolatore, il programma viene installato con le librerie base che contengono i comandi e le funzioni matematiche può comuni, nel caso in cui una determinata funzione non è presente nelle librerie, l’utente può includere altre librerie o creare la funzione desiderata scrivendo passo dopo passo l’algoritmo della funzione. Nel nostro caso useremo la funzione Polyfit la quale purtroppo non è presente nelle librerie standard e che quindi creeremo. Selezionando dal menù applicazioni SciNotes, si aprirà un editor di testo nel quale scriveremo le istruzioni che compongono la nostra funzione, per quanto riguarda queste ultime ho leggermente modificato un listato trovato in rete, trascurando i dettagli dell’algoritmo ci soffermeremo invece sulle caratteristiche comuni a tutte le funzioni ovvero la prima e l’ultima riga le quali delimitano l’inizio e la fine di ogni funzione. Nella prima riga è contenuto il nome della funzione (polyfit), è buona norma dare lo stesso nome al file ed alla funzione, che sarà quindi il nome da richiamare poi dalla console, inoltre sempre nella prima riga vengono definiti gli argomenti della funzione (x, y, n), nonché i valori d’uscita di quest’ultima (p). Adesso, una volta scritta la funzione, basta salvarla nella directory di lavoro per poi poterla comodamente richiamare dalla console o all’interno di un’altra funzione. Ritornando agli argomenti di polyfit, sono tre, (x, y) che rappresentano le coordinate ordinate dei punti che si vuole interpolare ed (n) che rappresenta il grado del polinomio d’interpolazione desiderato. Le curve di fitting, infatti, vengono restituite in forma di polinomi di grado n scelto dall’utente, così se n=1 la funzione restituirà i coefficienti (a e b) della retta y = ax + b, passante in prossimità dei punti dati, se n = 2 si avranno i coefficienti della parabola y = ax² + bx + c, se n=3 della cubica e così via, maggiore è il valore di n, maggiore sarà il grado di accuratezza della curva di fitting. In questa sede vedremo un esempio pratico della tecnica di interpolazione della curva di accuratezza e della tecnica di compensazione considerando un comune sensore di temperatura, ovvero l’integrato MCP9700. Dal foglio specifiche di quest’ultimo, prendiamo in considerazione la curva d’accuratezza (Figura 1), sull’asse delle ascisse viene riportato il valore reale della temperatura in gradi, mentre sull’asse delle ordinate viene riportato l’errore presente sulla misura a quella temperatura, ad esempio, ad una temperatura reale di 25° il sensore restituirà una lettura di 24.5° in quanto l’errore a 25° è -0.5°, mentre ad una temperatura reale di 110° il sensore restituirà una temperatura di 110°.
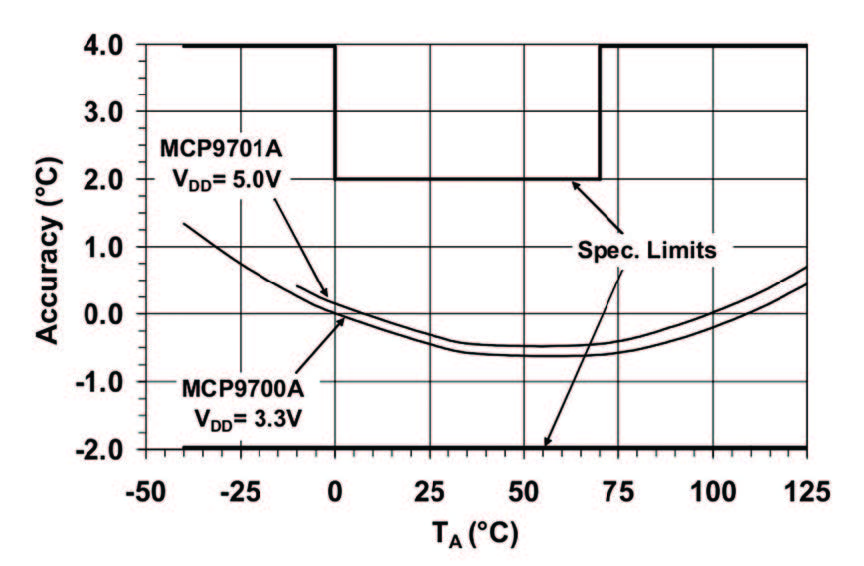
Figura 1: Curva di Accuratezza del Sensore
Per interpolare la curva mostrata in figura vengono considerati alcuni punti di quest’ultima e sistemati ordinatamente in due vettori (X e Y), che verranno poi riutilizzati su Scilab, quindi ad esempio considerando 6 generici punti della curva X = [-25, 0, 25, 50, 75, 100]; Y = [0.7, 0.05 , -0.3, -0.35, -0.2, 0.25] ed interpolando con un polinomio del primo grado la funzione ci restituirà una retta, (Figura 2). Questa soluzione è molto lontana dalla reale curva, mentre interpolando con un polinomio di secondo grado la funzione restituirà una parabola, la quale ha un andamento (Figura 3) abbastanza simile alla curva reale.
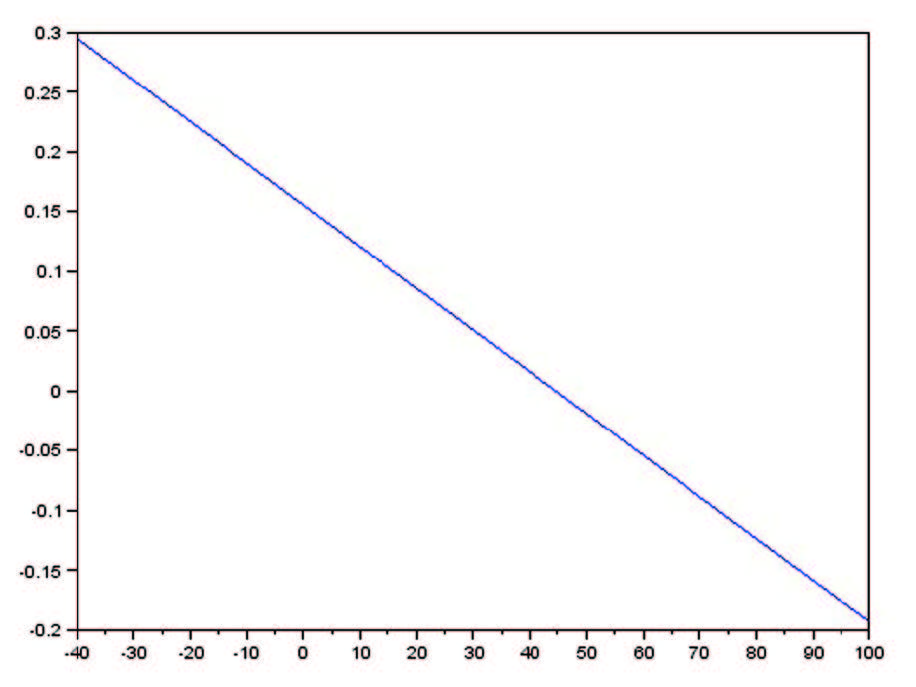
Figura 2: Interpolazione Tramite Retta
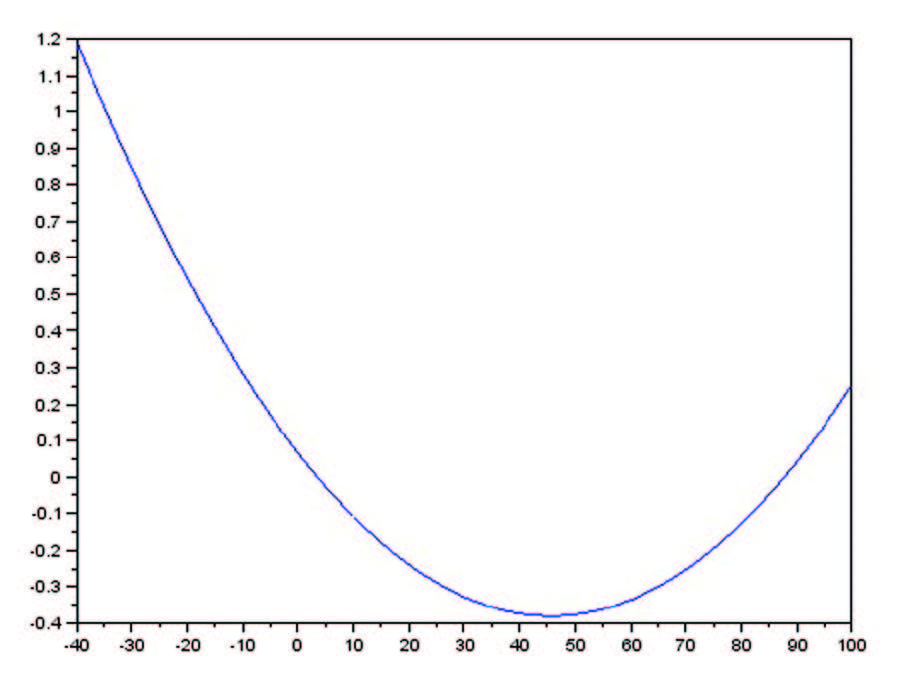
Figura 3: Interpolazione Tramite Parabola
Quindi, indicando con x il valore reale della temperatura, il valore y letto dal sensore sarà dato dalla temperatura reale meno un fattore d’errore (precedentemente interpolato come una curva del secondo grado funzione della temperatura reale), ad esempio nel nostro caso il sensore restituirà y = x-Errore = x-0.0002x2+0.0196x-0.0664 dove, come già detto, i coefficienti dell’errore sono stati ottenuti dall’interpolazione della curva d’accuratezza. A questo punto il calcolo della temperatura reale si riduce alla semplice soluzione di un'equazione di secondo grado:
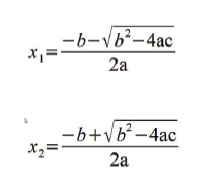
nel nostro caso i coefficienti dell’equazione di secondo grado sono:
a = -0.0002
b = 1+0.0196= 1.0196
c = y-0.0664
quindi, leggendo un valore di temperatura e utilizzando la soluzione generica dell’equazione di secondo grado si ottiene la temperatura reale, va notato che trattandosi di un'equazione di secondo grado, le soluzioni saranno due, ma soltanto una si troverà all’interno del campo delle temperature realmente misurabili dal sensore.
function p = polyfit(x,y,n) m = lenght(x) if lenght(y) <> m error(‘x and y must have same lenght’), end v = ones(m,n+1) for i=2:n+1, v(:,i) = x.^v(:,i-1),end p = (v/y)‘ end
| Listato 1 |
COMPENSAZIONE MEDIANTE UN MICROCONTROLLORE
Trovata la funzione che descrive al meglio la curva di accuratezza del nostro sensore, vediamo un semplice esempio di pseudo-codice da implementare sul microcontrollore per la compensazione della temperatura, supponendo di aver salvato il valore letto dal sensore, in gradi centigradi, nella variabile lettura, per il sensore MCP9700, l’algoritmo di compensazione sarà del tipo illustrato nel listato 2:
tmax = 125; //temperatura massima nel range del sensore
tmin = -50; //temperatura minima nel range del sensore
a = -0.00021; //a,b,c coefficienti della curva d’accuratezza
b = 0.01956;
c = -0.06643;
x1 = (-(1+b)-sqrt((1+b)*(1+b)-4*a*(-lettura+c)))/2*a;
x2 = (-(1+b)+sqrt((1+b)*(1+b)-4*a*(-lettura+c)))/2*a;
if ((x1<tmax) && (x1>tmin) { temperatura = x1;}
else { temperatura = x2;}
| Listato 2 |
Questo listato dal punto di vista computazionale è molto semplice, l’operazione più complessa è una radice quadrata e quindi si può implementare su quasi tutti i tipi di microcontrollore disponibili in commercio. In figura viene riportata la curva d’accuratezza del sensore usato in assenza di compensazione (curva blu) e dopo la compensazione (curva verde), si vede bene che in caso di compensazione la curva si riduce ad una retta prossima all’asse delle ascisse, maggiore è il grado di precisione dell’interpolazione maggiore sarà la compensazione.
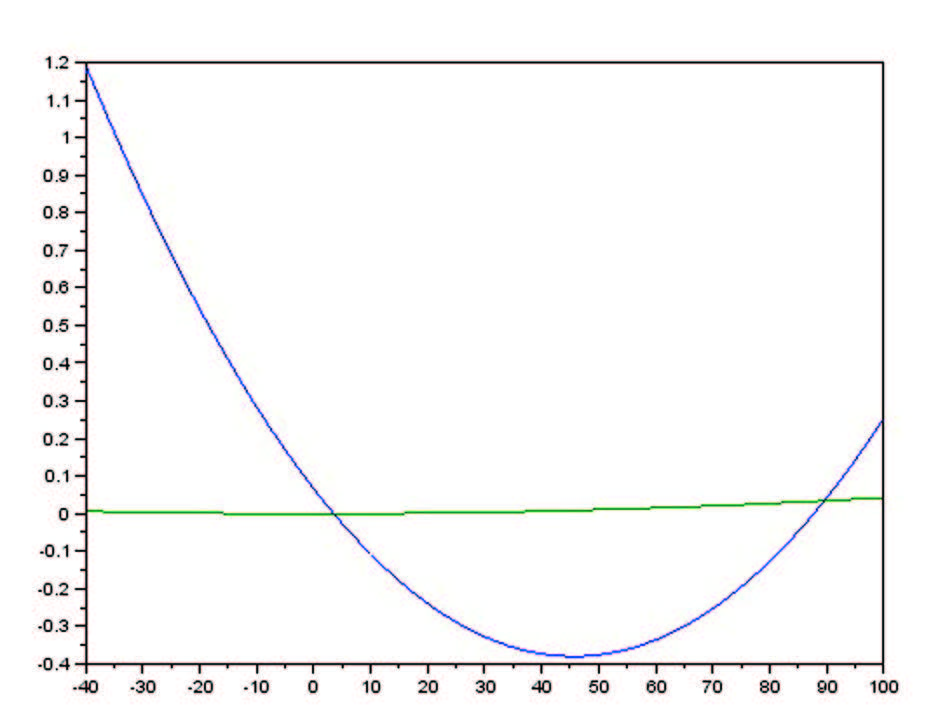
Figura 4: Confronto fra le Curve
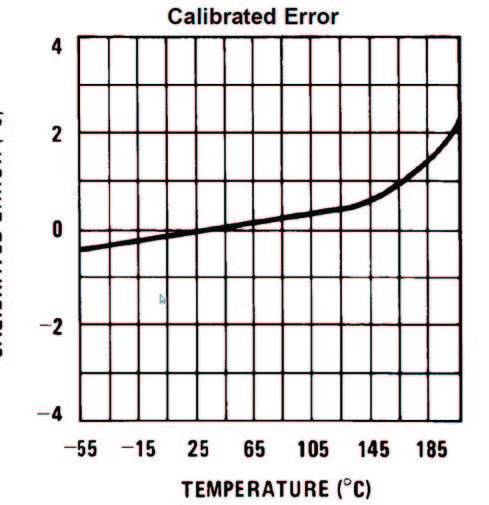
Figura 5: Curva di Errore vs. Temperatura
CONCLUSIONI
Lo scopo di questo articolo era quello di definire delle strategie per la compensazione dell’accuratezza dei sensori partendo dalle apposite curve presenti nei fogli delle specifiche dei sensori stessi. In questo articolo ci siamo occupati dei sensori di temperatura, ma è chiaro che le tecniche di interpolazione valgono per qualsiasi insieme di punti e che, una volta compreso come ottenere i coefficienti dei polinomi che approssimano le curve, con un piccolo sforzo computazionale si può compensare qualsiasi effetto indesiderato presente sulla lettura del sensore.