
Da qualche anno a questa parte le reti neurali sono passate da pura curiosità accademica, a settore di intensa ricerca, a santo Graal per qualsiasi applicazione. Chi non sa cosa siano come minimo ne ha sentito parlare, e chi ha una vaga idea di a che cosa servano le vuole per la sua particolare applicazione. E anche a ragione: a fronte di richieste hardware tutto sommato al giorno d’oggi tollerabili (che vuoi che sia una GPU in più?), le reti neurali si sono dimostrate molto efficaci nella soluzione di parecchi tipi di problemi. Uno dei settori in cui si sono dimostrate particolarmente in gamba è quello del riconoscimento di oggetti (sì, sono loro che disegnano il rettangolino attorno alla macchina su quel video che YouTube ti ha consigliato l’altro giorno) e oggi vi parleremo di uno dei top player di questo mercato: YOLO.
DAL PARTICOLARE AL GENERALE
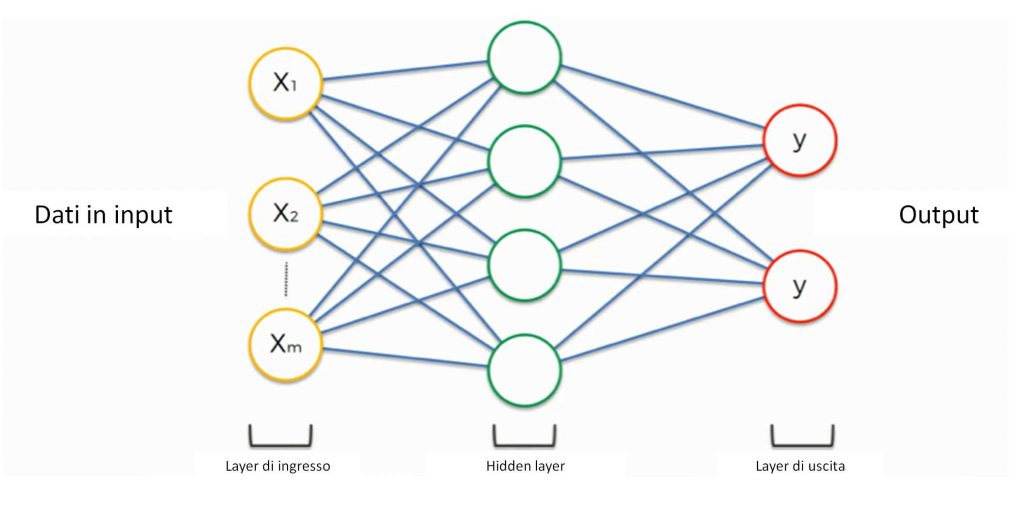
Figura 1: Una generica rete neurale
Una rete neurale è un oggetto concettualmente molto semplice: come il nome suggerisce, si tratta di una rete fatta di neuroni (d’ho!) Detta in maniera meno banale, si tratta di una serie di unità di calcolo (i neuroni) collegati tra loro in una rete, come nella Figura 1. Ogni pallino rappresenta un neurone, e ogni neurone esegue qualche calcolo. A seconda di quanti strati di neuroni ci possono essere nella rete, parleremo di “deep” neural network (DNN, se di strati ce ne sono tanti) o di “shallow” neural network (se non ne abbiamo più di uno o due). Dunque, per progettare una rete neurale bisogna sia decidere che calcoli deve fare il singolo neurone, sia come connettere i neuroni tra loro. Attenzione: “che calcoli” significa più precisamente “che tipo di calcoli”, ad esempio una scalatura o un’arcotangente; di quanto si scali o se l’arcotangente ha qualche coefficiente davanti non sta al progettista deciderlo - sarà la rete stessa a sceglierseli da soli durante la fase di addestramento.
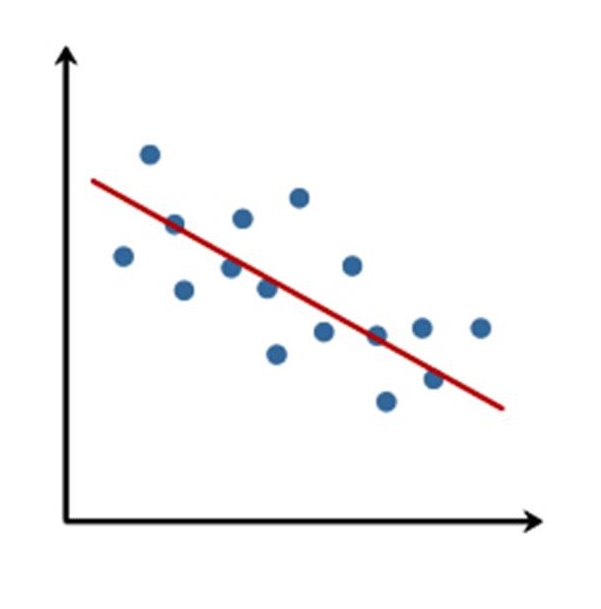
Figura 2: Regressione lineare
Ora, il calcolo più semplice che un neurone può eseguire (e quello che in genere gli viene fatto eseguire) è la regressione lineare. Stiamo parlando di ciò che accade nella Figura 2: dato un insieme di punti, un algoritmo di regressione lineare trova la retta che meglio approssima l’andamento dei punti. Trovare questa retta rappresenta un modo molto semplice per generalizzare a partire da un certo numero di esempi. Se ad esempio i punti rappresentassero il prezzo di una casa in funzione della sua metratura, nota la retta si potrebbe stimare il prezzo di una casa con metratura non fornita nell’insieme noto. In estrema sintesi (e, che ci crediate o no, senza nemmeno semplificare troppo) una rete neurale fa poco più di questo: presi alcuni esempi, ne ricava la funzione che meglio li approssima (“impara” da essi) e poi usa questa funzione per stimare una qualche caratteristica di un input che non ha mai esaminato prima.
È chiaro che un singolo neurone che esegue una regressione lineare non ci potrà dare più di tanto: già se volessimo sapere il prezzo di una casa in funzione della metratura e dell’anno di costruzione, la singola regressione sarebbe insufficiente. Che possiamo fare? Bè, aggiungere altri neuroni, no? L’approccio ha senso. Più sono le caratteristiche di cui vogliamo tenere conto (le “features” dell’input), più neuroni in parallelo ci serviranno.
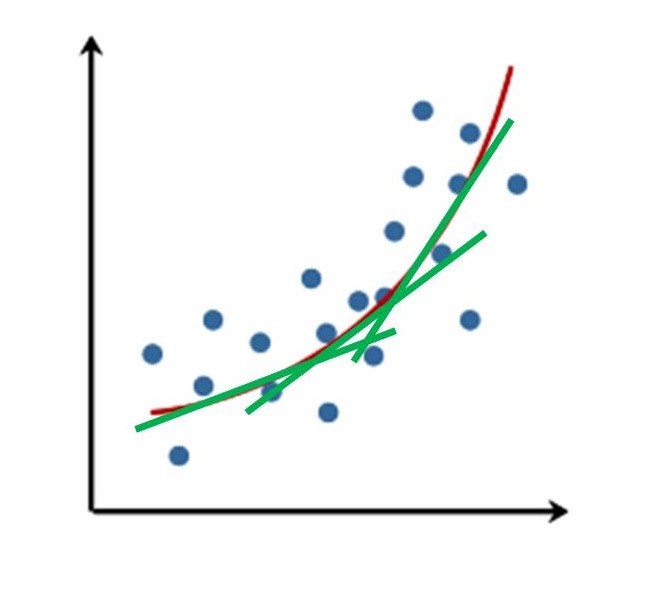
Figura 3: Più regressioni lineari approssimano una parabola
E dovrebbe essere chiaro anche che la regressione lineare è limitata intrinsecamente per quello che può approssimare correttamente. Per dirne una, una parabola non viene bene se la approssimiamo con una retta. Però, una parabola possiamo approssimarla con una successione di rette, come nella Figura 3. Questa è l’idea dietro l’aggiunta di nuovi strati (layer, in questo contesto) di neuroni dopo il primo, e il motivo per cui probabilmente avrete sentito parlare solo dell’apprendimento profondo, e non di quello shallow - quello profondo funziona meglio.
L’apprendimento profondo ha però una serie di problemi. Uno, si può dimostrare che mettere in cascata una serie di regressioni lineari non modella qualcosa di non lineare come può essere una parabola, ma rimane, nel complesso, una cosa lineare. Come non si possono tirar fuori delle pere da un cesto di mele, così non si può far comparire della non linearità giocando solo con oggetti lineari. Fortunatamente, questo problema è semplice da risolvere: basta aggiungere, tra uno strato e l’altro, delle non linearità! Stiamo parlando delle cosiddette funzioni di attivazione. Se avete mai bazzicato in questo settore, esponenti celebri di questo mercato sono la ReLU o il sigmoide. Non stiamo qui a soffermarci troppo sulla differenza tra i vari tipi - basti sapere che ci sono e che devono esserci perché senza di esse le reti non si comporterebbero particolarmente bene.
Il secondo (e molto più serio) problema è che le DNN sono pesanti. Dal punto di vista di carico computazionale e di occupazione di memoria, intendo. Dipende molto da quante features vogliamo considerare e da quanti layer ci sono nella rete, ma i coefficienti delle varie regressioni lineari potrebbero essere tantissimi. Ad esempio, supponiamo di voler applicare una DNN ad un’immagine. I coefficienti in ingresso, x, sarebbero i pixel dell’immagine. Se l’immagine fosse, diciamo, 300x300, avremmo in totale n neuroni e il doppio dei coefficienti! E questo solo per il primo layer! Si tratta di una marea di coefficienti e di un numero spropositato di calcoli da fare, e tra l’altro per un’immagine che, nell’epoca del full-HD, non fa una gran figura.
È su questo scoglio che le DNN si sono arenate per un pò, almeno fino a quando…
QUESTA BISTRATTATA CONVOLUZIONE
…fino a quando qualcuno non si è reso conto che si potevano ottenere risultati straordinariamente migliori tirando in ballo una delle operazioni fondamentali dell’elaborazione dei segnali: la convoluzione. La convoluzione è l’operazione alla base dei filtraggi. Anche se magari quando si sente la parola “filtro” la prima cosa cui si pensa è la trasformata di Fourier e la moltiplicazione in frequenza, l’altro lato della medaglia, ossia il filtraggio come convoluzione nel tempo\spazio è quello più operativo. In pratica, di norma nel campo della computer vision un filtraggio si implementa come una convoluzione, non come una trasformata di Fourier seguita da moltiplicazione.
Ma che c’entrano i filtraggi qui? Riflettiamo un attimo sul senso di quello che stiamo cercando di fare. La rete, per fare ciò che deve, esamina delle caratteristiche dei dati e le elabora per trarne certe conclusioni. Dunque, la prima cosa che la rete deve fare è ricavare, estrarre le caratteristiche che le servono. Se stiamo lavorando con delle immagini, un filtraggio rappresenta un modo molto efficiente per farlo. Pensiamo ad una rete progettata per riconoscere dei volti. Un volto è fatto da un certo numero di tratti, ad esempio occhi, naso e bocca. Un occhio ha una forma prevalentemente circolare, mentre un naso lo possiamo vedere come (a grandi linee) un paio di linee parallele che vanno dall’alto verso il basso. Distinguere tra questi due casi è piuttosto semplice: basta esaminare i bordi! E i bordi possono essere estratti semplicemente mediante una convoluzione con una matrice 3x3. La cosa veramente bella è che questa matrice 3x3 è la stessa per tutti i pixel, dunque non abbiamo bisogno più di un diverso neurone per ogni pixel, ognuno con la sua coppia di coefficienti: ci bastano 9 coefficienti in comune tra tutti i pixel! Rispetto ai 270000 di prima è un bel guadagno! Meno coefficienti significa meno memoria, meno calcoli, e tempi di training inferiori. Non male, per un operatore che tutti ci siamo affrettati a dimenticare.
Senza troppa fantasia, le reti che, per ogni layer, calcolano delle convoluzioni, vanno sotto il nome di Reti Neurali Convoluzionali, o CNNs (Convolutional Neural Networks, da non confondere con l’emittente televisiva), e sono in breve diventate tremendamente popolari per le applicazioni di image processing e computer vision, al punto da costituire l’ossatura praticamente di tutte le reti di maggior successo usate in questo campo. [...]
ATTENZIONE: quello che hai appena letto è solo un estratto, l'Articolo Tecnico completo è composto da ben 2687 parole ed è riservato agli ABBONATI. Con l'Abbonamento avrai anche accesso a tutti gli altri Articoli Tecnici che potrai leggere in formato PDF per un anno. ABBONATI ORA, è semplice e sicuro.







Bella la teoria, ma senza esempi diventa studio.
Non mi sembra sia lo scopo di una rivista farci ritornare a scuola.
Saluti
CG