Questo articolo introduce il lettore alle funzionalità offerte dallo strumento di calcolo e di simulazione matematica Octave, un progetto open source liberamente utilizzabile. Verranno, inoltre, presentati esempi pratici di applicazione dello strumento stesso.
Octave è uno strumento di programmazione numerica disponibile sotto la licenza per il software libero GNU GPL (General Public License). Si tratta di un’applicazione dotata di funzionalità avanzate, molto potenti e versatili, con un buon grado di compatibilità (anche se non completo) con il più blasonato strumento Matlab. Matlab, abbreviazione di “Matrix Laboratory”, è attualmente il software di programmazione numerica proprietario commercialmente più diffuso al mondo. Viene, infatti, utilizzato da numerose università, centri di ricerca, aziende pubbliche e private, o da semplici utilizzatori e appassionati di matematica. Alla sua diffusione e popolarità contribuisce anche la disponibilità di una versione speciale per studenti (Matlab Student Edition) dal costo particolarmente competitivo. Matlab è fondamentalmente un linguaggio di scripting del tutto simile a Perl, Python e PHP, corredato con un insieme completo e ampiamente integrato di funzioni numeriche, matematiche, statistiche, e grafiche. Sono, ad esempio, incluse funzioni come la trasformata di Fourier, l’inversione di matrice e gli istogrammi. Matlab è stato originariamente sviluppato alla fine degli anni 60 come un front-end interattivo e semplice da usare per l’utilizzo di librerie Fortran relative all’algebra matriciale e alla manipolazione di matrici. Successivamente, negli anni 80, Matlab fu riscritto completamente in linguaggio C e diventò un prodotto commercializzato dalla società MathWorks. Nel corso degli anni, Matlab si è evoluto sempre più, fino a supportare array numerici multidimensionali, stringhe di caratteri, altre funzionalità matematiche e anche la programmazione orientata agli oggetti.
OCTAVE
Octave è stato sviluppato da John W. Eaton insieme ad altri studenti come una valida alternativa free al prodotto commerciale Matlab. Deve il suo nome a un docente dell’Università del Texas, di cui Eaton a quei tempi era allievo. Octave condivide con Matlab la maggior parte delle funzioni e la loro sintassi, il che lo rende adatto all’utilizzo per un’ampia gamma di applicazioni matematiche e numeriche. Esso è disponibile sia sotto forma di codice sorgente, sia come applicazione in forma binaria pre-compilata per vari sistemi operativi, tra cui Windows, Mac OS X e Linux/Unix. Octave include delle funzioni integrate per la gestione di file dati delimitati con il carattere TAB oppure con il separatore virgola (file di tipo Comma Separated Values, o CSV). Queste funzioni sono molto utili, in quanto permettono a Octave di interfacciarsi in modo semplice e diretto con altri programmi e applicazioni. Inoltre, Octave può leggere e scrivere direttamente i file di tipo binario, attraverso funzioni del tutto simili a quelle di un linguaggio ad alto livello come il C: esistono, infatti, le funzioni fopen, fread, fwrite, e fclose. Funzioni di questo tipo sono particolarmente utili per applicazioni avanzate nel settore audio, come ad esempio il riconoscimento del linguaggio parlato. Octave include anche funzioni di manipolazione di file in formato non compresso Microsoft WAV (funzioni wavread e wavwrite). Octave supporta poi un meccanismo molto semplice per integrare funzioni compilate, scritte in linguaggi ad alto livello come C, C++, o Fortran, attraverso il comando mkoctfile. Essendo un linguaggio di scripting, Octave include le istruzioni tipiche di questi linguaggi, come le strutture condizionali, i cicli e le dichiarazioni di funzioni.
QUALCHE ESEMPIO PRATICO
L’installazione del programma è molto semplice: basta, infatti, scaricare il pacchetto per la piattaforma desiderata dal sito web indicato (gli esempi seguenti faranno riferimento alla versione 3.2.4 per il sistema operativo Windows) e seguire le istruzioni per l’installazione. Una volta lanciato, il programma presenterà una finestra simile a quella visibile in Figura 1, in pratica una shell attraverso la quale si possono impartire i comandi in modalità testo. Si tenga, inoltre, presente che è disponibile un help in linea, richiamabile attraverso il comando help, e un manuale completo online disponibile all’indirizzo citato nei riferimenti. Vediamo ora qualche esempio pratico di applicazione di Octave.
Figura 1: Octave in esecuzione
SOMMA DI VETTORI
Consideriamo come primo esempio la somma di due vettori (a e b) composti di tre elementi ciascuno. Si osservi la Figura 2: i primi due comandi servono a definire il contenuto dei due vettori, mentre il terzo esegue l’operazione di somma vera e propria. Octave evidenzia il risultato ottenuto tramite il termine “ans”, abbreviazione di answer; è anche possibile, in ogni momento, richiamare a video il risultato dell’ultima operazione eseguita tramite lo stesso comando “ans”. Si noti, inoltre, come in Octave la dimensione della matrice sia determinata automaticamente, e pertanto non sia necessario esplicitarla.
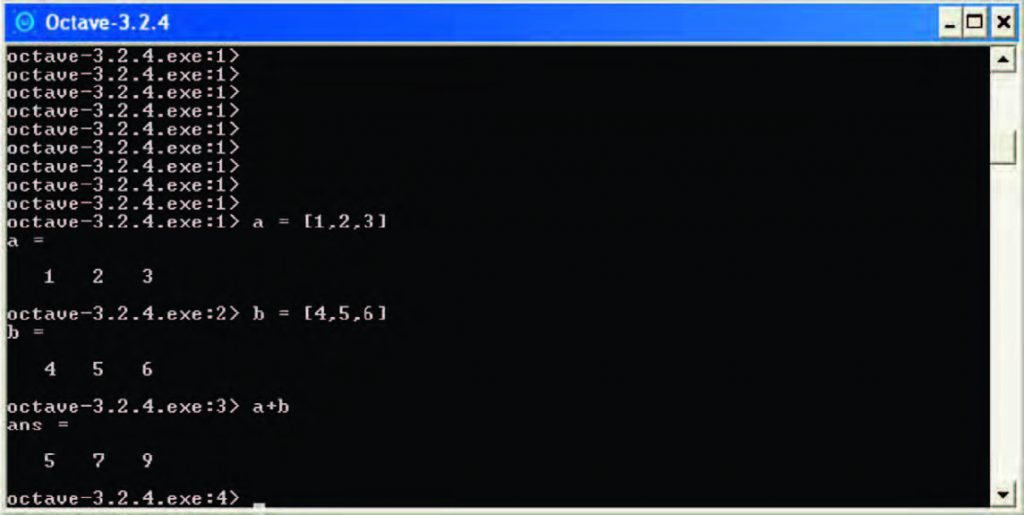
Figura 2: somma di due vettori
PRODOTTO DI MATRICI
Indichiamo con a e b due matrici a due righe e due colonne ciascuna (quindi 2x2), e supponiamo di voler determinare la matrice derivante dal prodotto di a per b. Tutte le operazioni richieste in Octave sono indicate in Figura 3, nella quale è visibile anche il risultato del prodotto. Va notato come, nella definizione di una matrice qualsivoglia, la virgola serve a separare gli elementi appartenenti a una stessa riga (si può, alternativamente, utilizzare anche il carattere spazio al posto della virgola), mentre il punto e virgola serve per separare gli elementi appartenenti ad una riga da quelli della riga successiva.
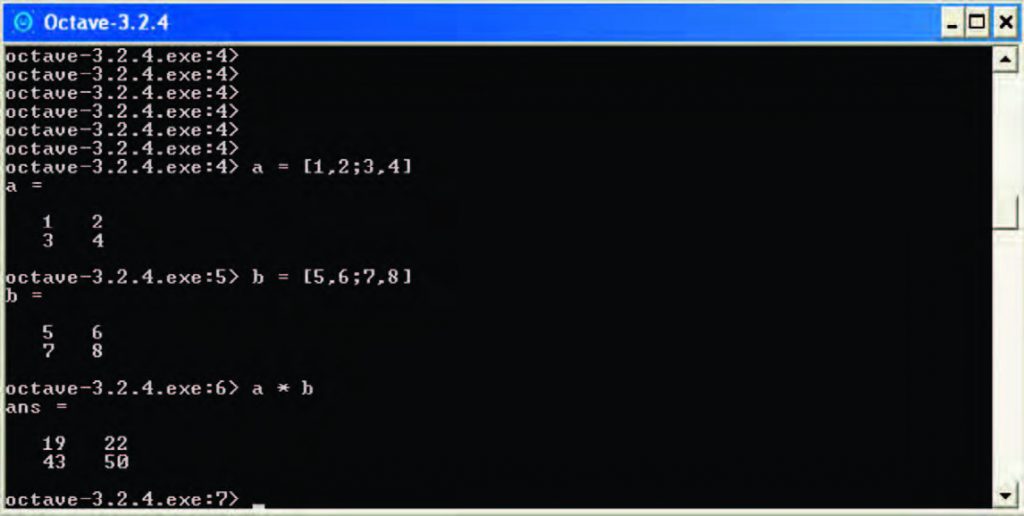
Figura 3: prodotto di due matrici 2x2
MATRICE TRASPOSTA, INVERSA E DETERMINANTE
La matrice trasposta di una matrice qualsiasi a si ottiene in Octave tramite il comando “a”. La matrice inversa di una matrice a si ottiene invece con il comando “inv(a)”, mentre il determinante si ottiene tramite il comando “det(a)”. Con riferimento alla matrice a definita in precedenza, i risultati corrispondenti sono visibili in Figura 4.
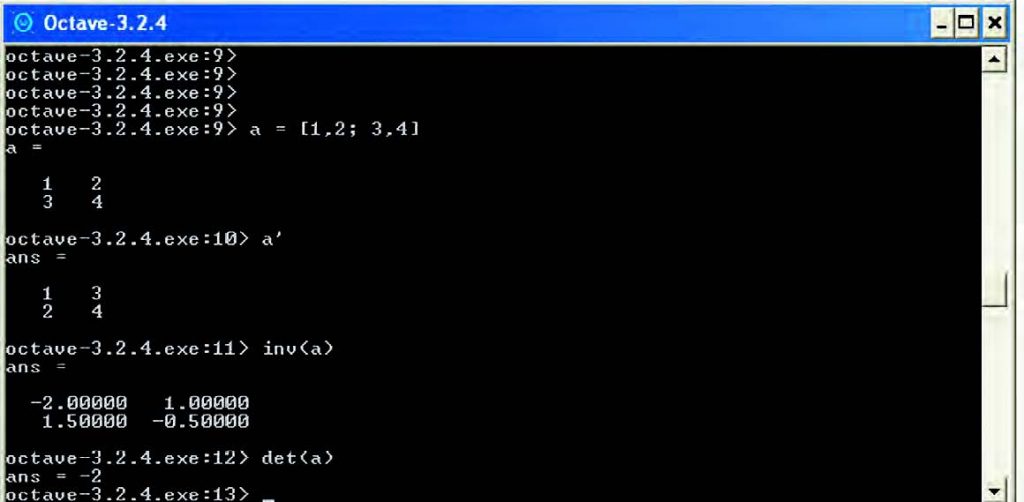
Figura 4: matrice trasposta, inversa, e determinante
SISTEMA DI EQUAZIONI LINEARI
Si tratta di un problema classico dell’algebra lineare, la cui soluzione grazie a Octave è particolarmente semplice e immediata. Si consideri come esempio il seguente sistema di tre equazioni lineari nelle tre incognite (x, y, z):
3*x1 + 5*x2 + x3 = 6
x1 - 8*x2 - x3 = -1
0.5*x1 + 4*x2 + x3 = 0
In forma vettoriale, il sistema può essere scritto come segue:
A * x = b
dove A è la matrice 3x3 dei coefficienti, x è il vettore 1x3 delle incognite (x1, x2, x3) e b è il vettore 3x1 dei termini noti. Applicando le regole dell’algebra matriciale (in particolare la regola di Cramer, a condizione che la matrice A sia invertibile, come in questo caso), la soluzione del sistema è la seguente:
x = A-1 * b
In Figura 5 è mostrata la soluzione del sistema attraverso Octave. Si noti come il risultato possa essere calcolato in due modi: attraverso il prodotto della matrice inversa di A per il vettore b, oppure attraverso la notazione tipica di Octave (e anche Matlab), A\b. A\b, infatti, equivale all’espressione A-1 * b, mentre A/b equivale all’espressione A * b-1.
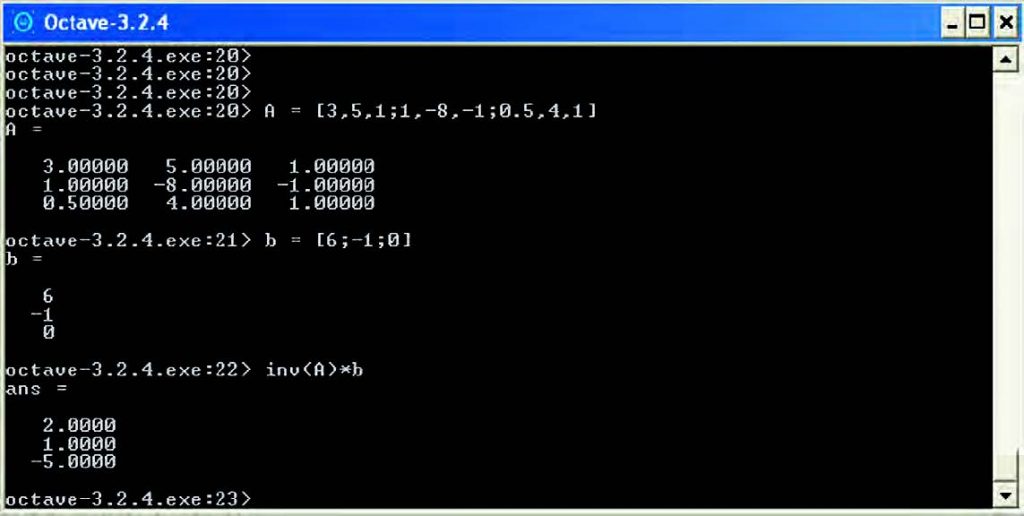
Figura 5: soluzione di un sistema di equazioni lineari
FUNZIONI STATISTICHE
Octave include numerose funzioni di statistica descrittiva, tra le quali citiamo la funzione “mean”, che permette di calcolare la media degli elementi appartenenti a un vettore o a una matrice, e prevede tra le opzioni il calcolo della media aritmetica, geometrica, oppure armonica. Come esempio, consideriamo il calcolo della media aritmetica di un vettore di cinque elementi di tipo double, come indicato in Figura 6 (l’opzione “a” indica di eseguire il calcolo della media aritmetica). Ricordiamo altre funzioni di statistica descrittiva, come ad esempio “median” (calcola il valore mediano degli elementi di un vettore), “std” (calcola la deviazione standard degli elementi di un vettore o di una matrice), “var” (calcola la varianza degli elementi di un vettore o di una matrice), e numerose altre funzioni per il calcolo della covarianza, correlazione, etc.
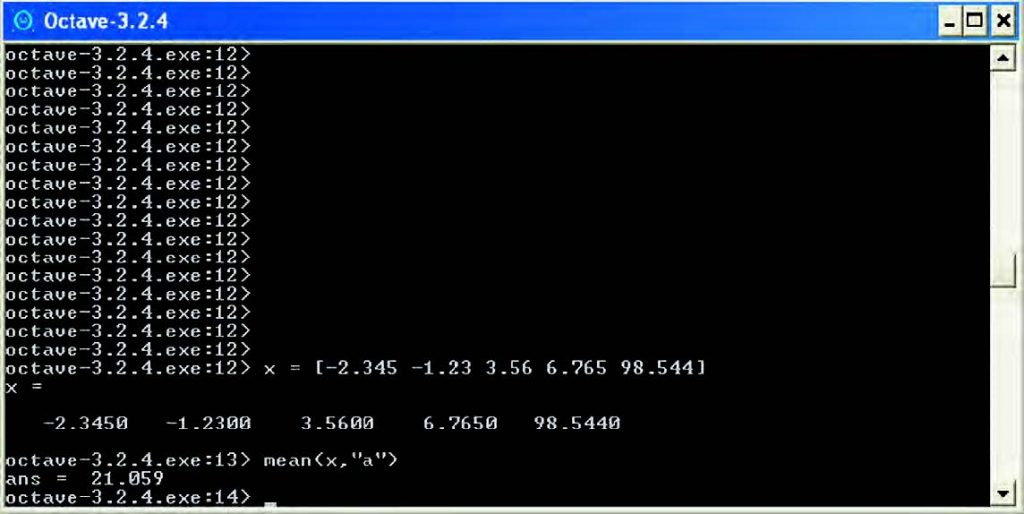
Figura 6: media aritmetica di un vettore di double
GRAFICI
Octave permette di tracciare agevolmente grafici in due o in tre dimensioni, una funzionalità molto utile, ad esempio, per esaminare l’andamento di una funzione, oppure per rappresentare graficamente una serie di dati prodotti da una simulazione. Per quanto riguarda la rappresentazione grafica, Octave si appoggia direttamente a gnuplot, un programma incluso nella distribuzione Octave e anch’esso distribuito con licenza GNU GPL.
GRAFICO A BARRE
Come primo esempio di rappresentazione grafica prendiamo in considerazione il classico “bar graph”, che in Octave possiamo rappresentare attraverso la seguente lista di comandi:
v = [4 7 1 11 20] # vettore di 5 elementi interi bar(v) # rappresentazione grafica a barre grid # attiva la visualizzazione griglia title “Grafico a barre” # titolo del grafico xlabel(“Elementi”) # etichetta asse x ylabel(“Valori”) # etichetta asse y
I comandi sono molto semplici e intuitivi, e penso non occorra alcun commento aggiuntivo, se non far notare che, in Octave, con il carattere “#” si indica l’inizio di un commento che prosegue sino al termine della linea. Il grafico risultante è visibile in Figura 7.
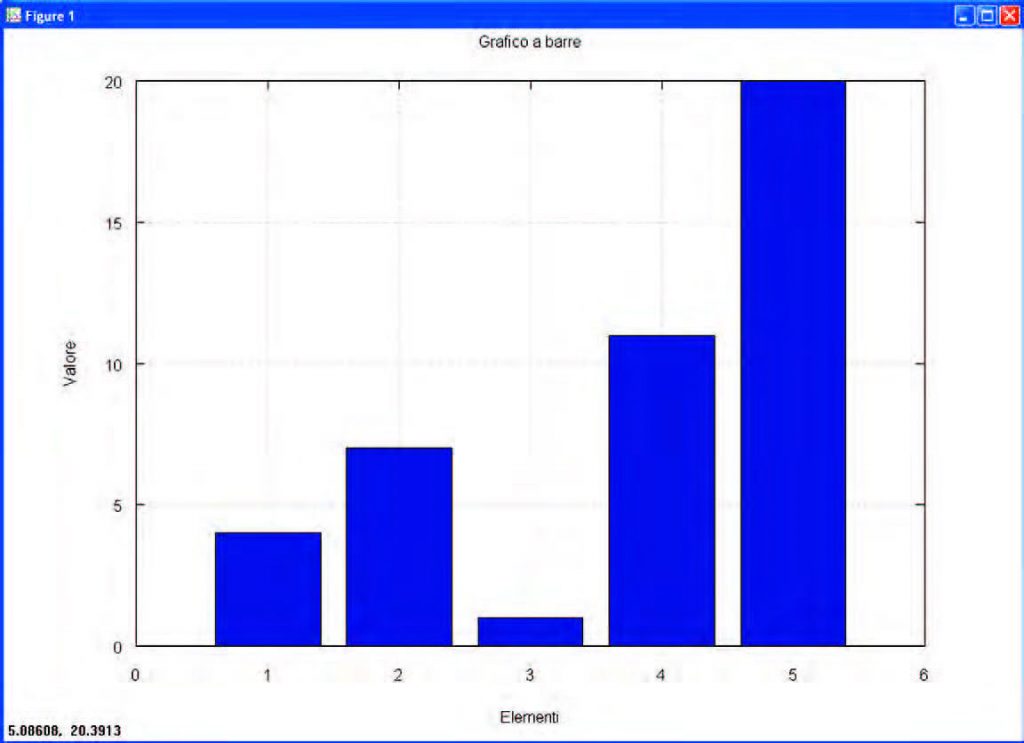
Figura 7: un grafico a barre
GRAFICO DI FUNZIONE IN 2D
Supponiamo ora di voler visualizzare il grafico della funzione trigonometrica sin(x), per x compreso tra –p e + p. La lista di comandi da fornire a Octave per ottenere il risultato desiderato è la seguente:
x = -pi:0.1:pi # range di valori di x (step=0.1) y = sin(x) # funzione da rappresentare plot(y) # comando di visualizzazione
title “Funzione trigonometrica seno”. Il grafico prodotto da Octave attraverso gnuplot è visibile in Figura 8.
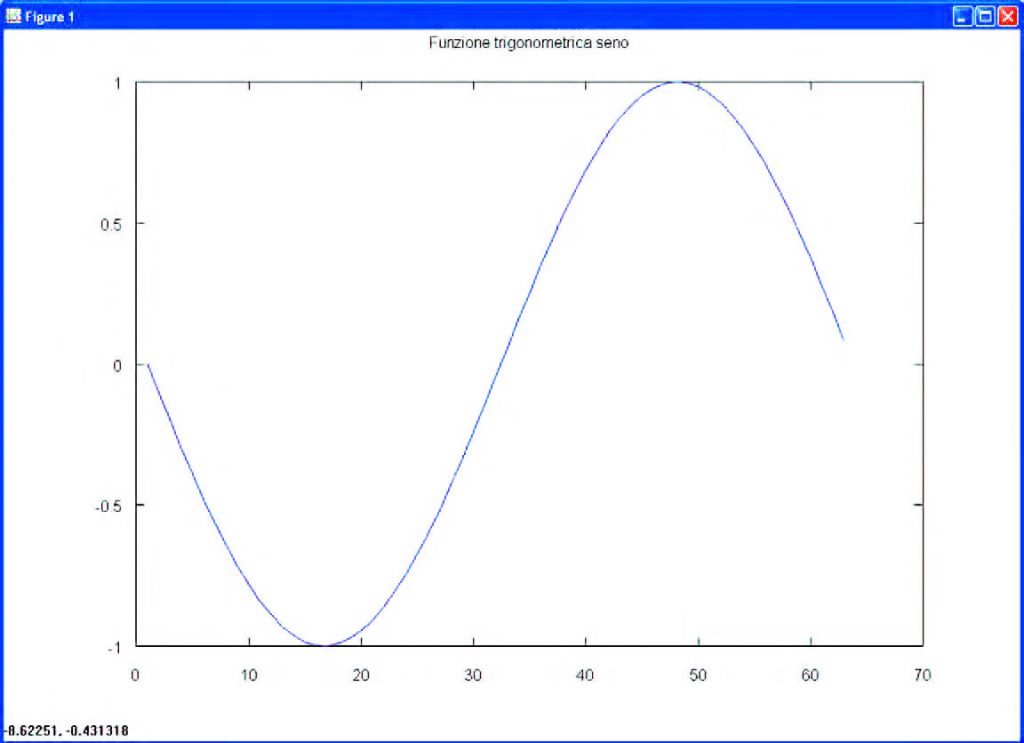
Figura 8: grafico di funzione in 2D
GRAFICO DI FUNZIONE IN 3D
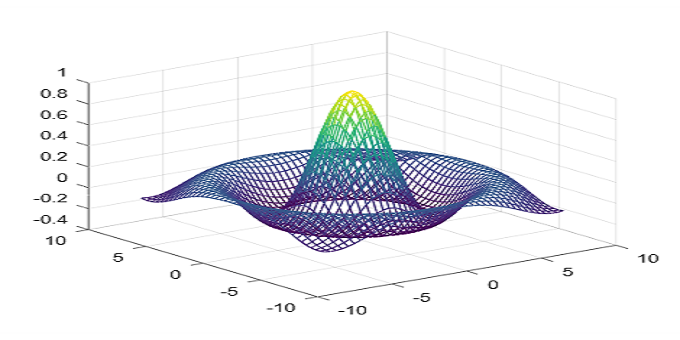
A titolo puramente dimostrativo, vediamo un esempio spettacolare di rappresentazione grafica in tre dimensioni, il cosiddetto "sombrero", che possiamo disegnare in Octave fornendo il semplice comando "sombrero", ottenendo il risultato visibile in Figura 9. Ricordiamo che tale grafico corrisponde alla rappresentazione in tre dimensioni della seguente funzione:
z = sin (sqrt (x^2 + y^2))/(sqrt (x^2 + y^2))
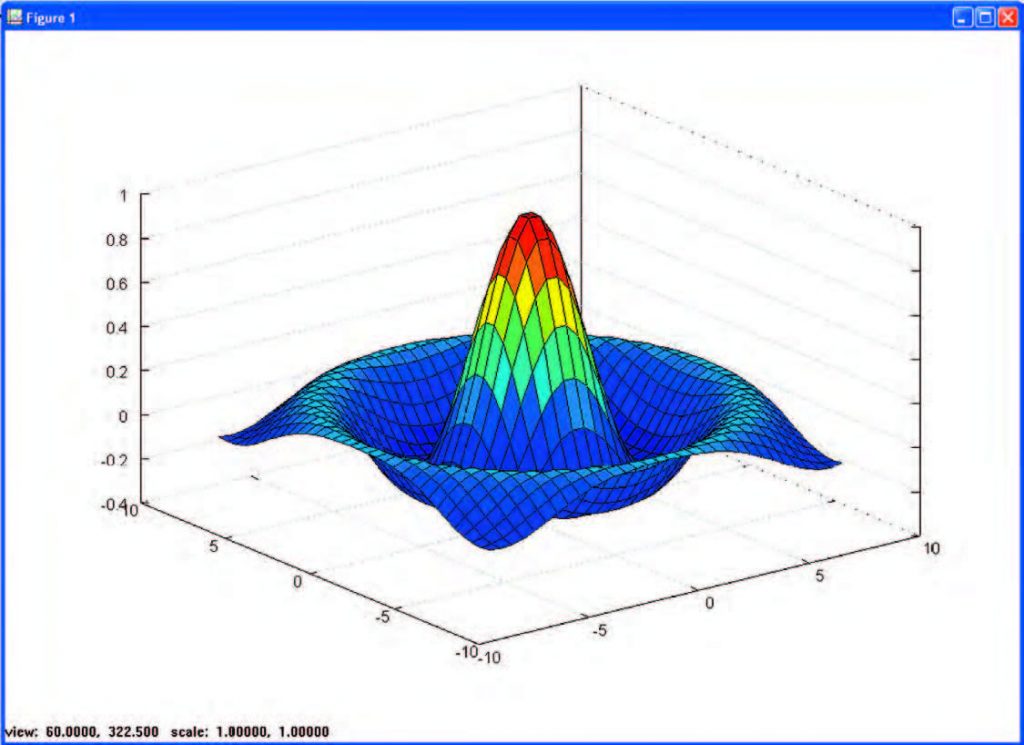
Figura 9: il "sombrero"
NUMERI COMPLESSI
Tra i numerosi oggetti matematici supportati da Octave, non potevano mancare i numeri complessi. La parte immaginaria può essere indicata in Octave, indifferentemente, con i oppure con j, per cui le seguenti definizioni di numeri complessi sono entrambe valide:
z1 = 3 + 4i
z2 = -4 + j
A questo punto si possono eseguire in Octave le operazioni desiderate sui numeri complessi definiti, come ad esempio la somma, la differenza e ogni altra operazione significativa:
octave-3.2.4.exe:40> z1=3+4i z1 = 3 + 4i octave-3.2.4.exe:41> z2=-4+j z2 = -4 + 1i octave-3.2.4.exe:42> z1+z2 ans = -1 + 5i octave-3.2.4.exe:43> z1-4*z2 ans = 19 octave-3.2.4.exe:44>
I numeri complessi possono anche essere rappresentati graficamente, ottenendo quello che viene anche chiamato diagramma di Argand. Supponiamo, ad esempio, di voler rappresentare graficamente sul piano complesso i numeri z1 e z2 precedentemente definiti. Sarà sufficiente impartire i seguenti comandi a Octave, ottenendo quanto visibile in Figura 10:
plot(z1,‘*’,z2,‘*’) axis([-5 5 -5 5]) text(3.2, 4, “z1”) text(-4.4, 1, “z2”) FFT (Fast Fourier Transform)
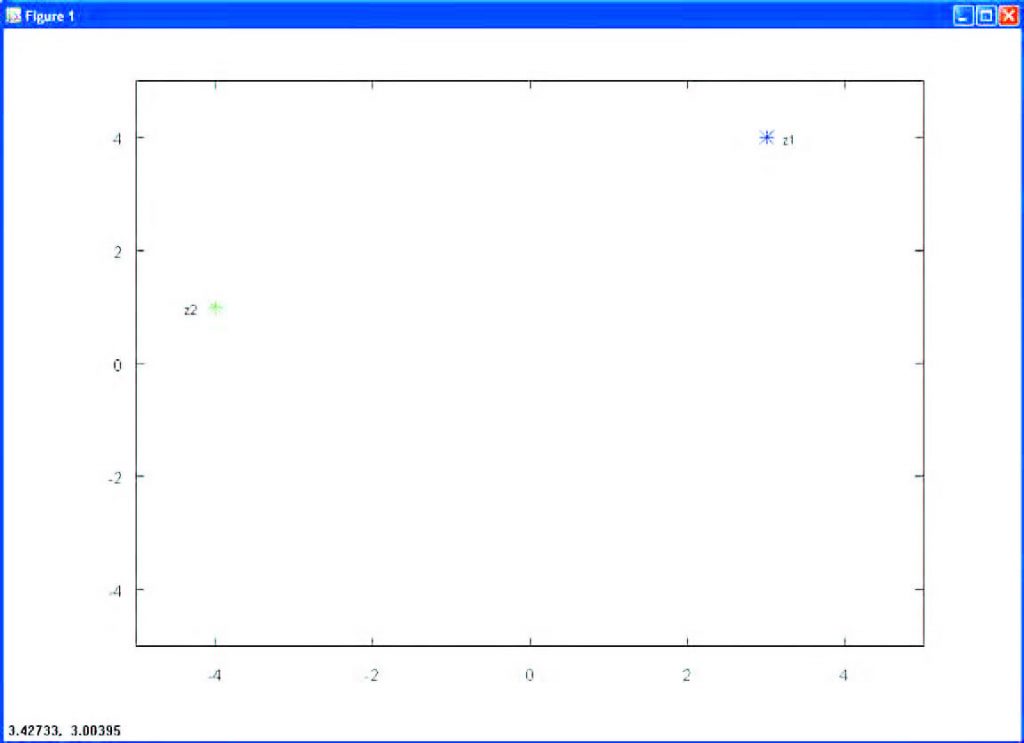
Figura 10: numeri complessi
La trasformata di Fourier veloce è un metodo efficiente per calcolare la trasformata di Fourier discreta (DFT) e la sua inversa. La trasformata di Fourier discreta serve a decomporre una sequenza di valori nelle sue componenti a frequenze diverse o, come si usa anche dire, serve per passare dal dominio del tempo a quello della frequenza. Dal punto di vista della complessità computazionale, l’algoritmo per il calcolo della DFT è troppo oneroso, e per questo motivo si preferisce ricorrere alla trasformata veloce, che ha, invece, una complessità computazionale inferiore. In Octave, la funzione Y = fft(x) restituisce la trasformata di Fourier discreta (DFT) del vettore x, calcolata basandosi proprio su un algoritmo di tipo FFT. Un utilizzo tipico della trasformata di Fourier consiste nel trovare, nel dominio delle frequenze, le componenti di un segnale fortemente disturbato nel dominio del tempo. Consideriamo come esempio un segnale campionato alla frequenza di 1 kHz, composto di una sinusoide a 50 Hz di ampiezza 0.7 e di una sinusoide a 120 Hz di ampiezza 1, e affetto da un rumore casuale a media nulla.
Fs = 1000; # frequenza di campionamento T = 1/Fs; # periodo di campionamento L = 1000; # lunghezza del segnale t = (0:L-1)*T; # vettore tempo #somma delle sinusoidi a 50 e a 120 Hz x = 0.7*sin(2*pi*50*t)+sin(2*pi*120 *t); y = x + 2*randn(size(t)); # sinusoide + rumore plot(Fs*t(1:50), y(1:50)) title(“Segnale corrotto con rumore casuale a media nulla”) xlabel(“tempo (millisecondi)”)
Il grafico corrispondente è visualizzato in Figura 11. È difficile identificare le componenti in frequenza guardando questo tipo di grafico. Passando, invece, nel dominio delle frequenze, è possibile identificare la trasformata di Fourier discreta del segnale y, affetto da rumore.
NFFT = 2^nextpow2(L); Y = fft(y, NFFT)/L; f = Fs/2*linspace(0,1,NFFT/2+1); plot(f,2*abs(Y(1:NFFT/2+1))) title(“Spettro di ampiezza di y(t)”) xlabel(“Frequenza (Hz)”) ylabel(“|Y(f)|”)
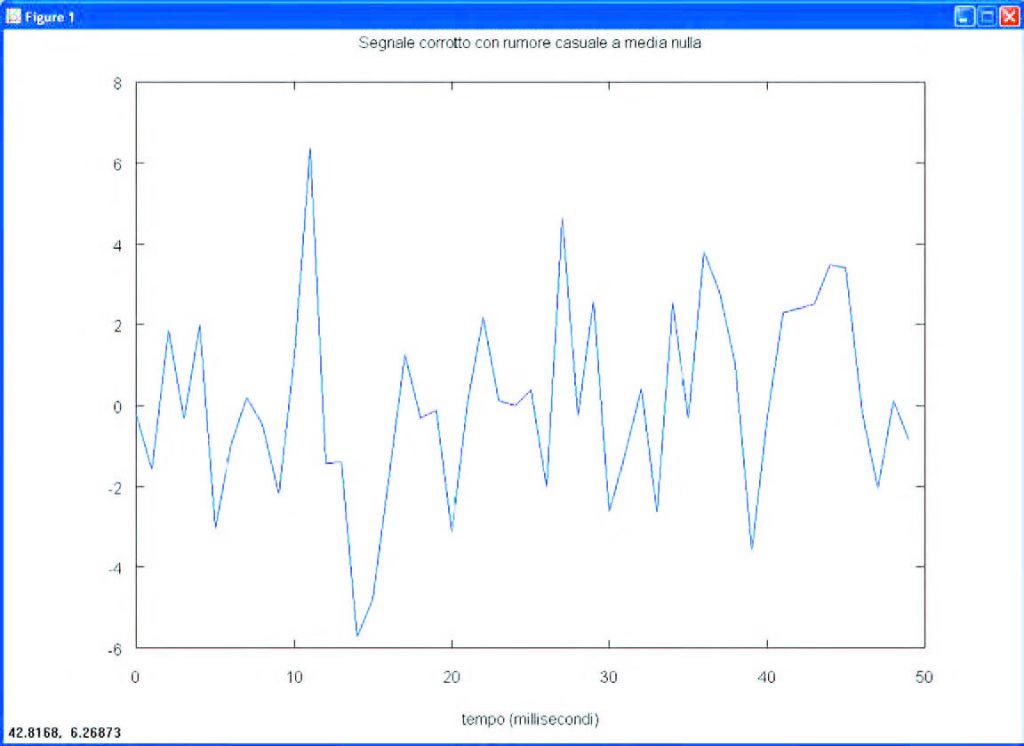
Figura 11: segnale corrotto da rumore casuale a media nulla
Il corrispondente grafico è visualizzato in Figura 12. Si osservi come siano facilmente individuabili le componenti a 50 e 120 Hz affette dal disturbo. Il motivo principale per il quale le ampiezze non sono esattamente pari a 0.7 e a 1 è dovuto alla presenza del rumore.
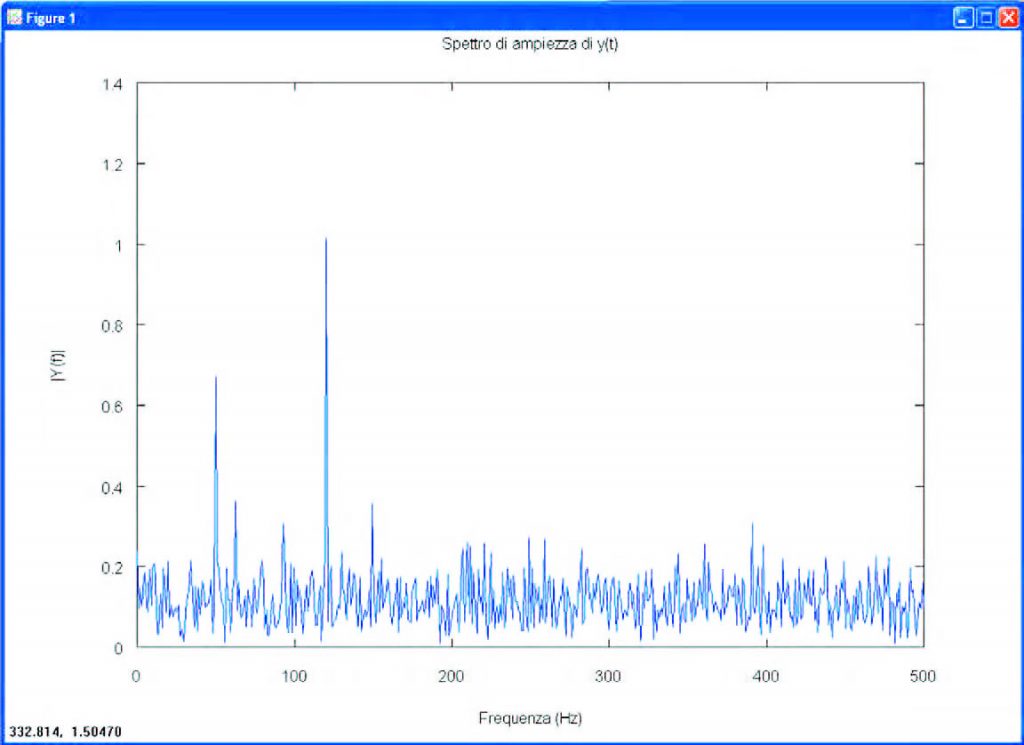
Figura 12: FFT
CONCLUSIONI
Per molte applicazioni e per molti utilizzatori, Octave rappresenta un’ottima alternativa a Matlab, o quantomeno un suo valido complemento. Qualche utilizzatore che impiega abitualmente Octave dispone anche di una licenza per Matlab; in questo modo può verificare se gli script creati con Octave sono o meno compatibili con Matlab, un aspetto molto importante da prendere in considerazione nel caso in cui si vogliano distribuire i propri script.




Ho utilizzato Octave e devo dire che per la parte matematica è molto simile a Matlab. Peccato che manca di Simulink