
Questo studio prende in esame alcune proprietà dei numeri naturali e risulta caratterizzato dalla presenza di due teoremi (consulta il seguente link per sapere di più sui "numeri"). Il primo teorema è inerente una disuguaglianza relativa a due sottoinsiemi relativi ad ogni insieme comprendente tutti i numeri naturali minori-uguali di un qualunque numero naturale maggiore di 1 mentre il secondo teorema riguarda la cardinalità di un particolare sottoinsieme di N. Infine verrà evidenziato come la struttura di N, secondo quanto definito in questo articolo e nel precedente, non sia propria solo della teoria dei numeri ma anche della fisica sub-nucleare.
INTRODUZIONE
Nel precedente studio abbiamo visto che l’insieme dei numeri naturali N può essere caratterizzato mediante 3 sottoinsiemi: il sottoinsieme generatore P*, il sottoinsieme W generato mediante la funzione moltiplicazione M così definita:
![]()
(secondo quanto enunciato dal Teorema fondamentale dell’aritmetica) ed il sottoinsieme I (non generabile a partire da P* mediante M). Sulla base di questa caratterizzazione possiamo enunciare il seguente teorema riportato nel paragrafo successivo.
PRIMO TEOREMA
Teorema 1 (Teorema sulla disuguaglianza della cardinalità primale). Dato un
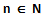
con n>1, l’ insieme Y(n) contente tutti gli elementi minori uguali ad n, risulta essere dato dall’unione tra un sottoinsieme non vuoto
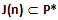
e di un sottoinsieme non vuoto
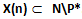
quindi
Non è mai possibile individuare un sottoinsieme
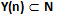
tale per cui
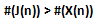
ovvero vale sempre la disuguaglianza:
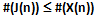
Inoltre si ha che:
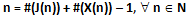
E’ altresì possibile definire una funzione vectcard (n):
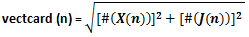
Dimostrazione. Dal Teorema dei numeri primi abbiamo che:
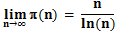
dove 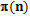 corrisponde al numero di numeri primi minori o uguali ad
corrisponde al numero di numeri primi minori o uguali ad 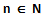
da cui segue che

Dato che
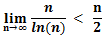
allora
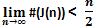
Siccome
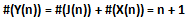
allora

quindi:
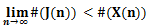
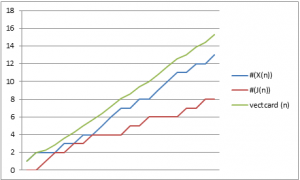
Nella figura 1 è riportato l'andamento della cardinalità degli insiemi J(n), X(n) e della funzione vectcard(n) per numeri naturali crescenti.
SECONDO TEOREMA
Teorema 2 (Teorema sulla disuguaglianza della cardinalità primale dell’insieme minimo o Teorema dell’insieme minimo). Dato un n ∈ N con n > 6, per qualunque sottoinsieme Y'(n) ⊆ Y(n) contenente tutti gli elementi compresi tra un valore minimo y'min ed un valore massimo y'MAX e con #(Y'(n)) > 7 vale la disuguaglianza:
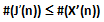
con
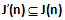
e
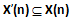
Ovvero:
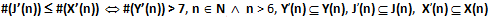
Dimostrazione. Consideriamo l’insieme Y(7). Tale insieme contiene l’unica sequenza di 2 numeri primi consecutivi (2, 3) seguita da una coppia di numeri primi gemelli (5, 7).
- Se noi considerassimo un sottoinsieme Y’(7) con cardinalità uguale ad 1 non saremmo sicuri di avere un sottoinsieme J’(n) tale per cui #(J’(n)) ≤ #(X’(n)) (esempio Y’(7)={2}).
- Se prendessimo in considerazione un sottoinsieme Y’(7) con cardinalità uguale a 2 ciò non garantirebbe di avere un sottoinsieme J’(n) tale per cui #(J’(n)) ≤ #(X’(n)) (esempio Y’(7)={2, 3}). Nel considerare un sottoinsieme Y’(7) con cardinalità uguale a 3 non saremmo sicuri di avere un sottoinsieme J’(n) tale per cui #(J’(n)) ≤ #(X’(n)) (esempio Y’(7) = {2, 3, 4}).
- Se individuassimo un sottoinsieme Y’(7) con cardinalità uguale a 4 ciò non garantirebbe di essere in presenza di un sottoinsieme J’(n) tale per cui #(J’(n)) ≤ #(X’(n)) (esempio Y’(7) = {2, 3, 4, 5}).
- Se noi considerassimo un sottoinsieme Y’(7) con cardinalità uguale a 5 non saremmo sicuri di avere un sottoinsieme J’(n) tale per cui #(J’(n)) ≤ #(X’(n)) (esempio Y’(7) = {2, 3, 4, 5, 6}).
- Se prendessimo in considerazione un sottoinsieme Y’(7) con cardinalità uguale a 6 ciò non garantirebbe di avere un sottoinsieme J’(n) tale per cui #(J’(n)) ≤ #(X’(n)) (esempio Y’(7) = {2, 3, 4, 5, 6, 7}).
- Se individuassimo un sottoinsieme Y’(7) con cardinalità uguale a 7 non saremmo sicuri di avere un sottoinsieme J’(n) tale per cui #(J’(n)) ≤ #(X’(n)) (esempio Y’(7) ={1, 2, 3, 4, 5, 6, 7}). Solo con un sottoinsieme Y’(7) avente cardinalità uguale a 8 siamo sicuramente in presenza di un sottoinsieme in cui vale la disuguaglianza #(J’(n)) ≤ #(X’(n)); infatti, in questo caso, Y’(7) ={0, 1, 2, 3, 4, 5, 6, 7} dove #(J’(n)) = 4 e #(X’(n)) = 4.
Dato che in N non esistono altri casi di una coppia di due numeri primi consecutivi seguita da una coppia di numeri primi gemelli, tale dimostrazione è valida per qualsiasi sottoinsieme Y'(n) con cardinalità maggiore di 7. Quindi la cardinalità minima di un sottoinsieme Y'(n) tale per cui #(J’(n)) ≤ #(X’(n)) è 8.
TEORIA DEI NUMERI E FISICA SUB-NUCLEARE
La caratterizzazione I P* W, vista fin qui, non è esclusiva della matematica; infatti anche i costituenti fondamentali che partecipano alla formazione dell’atomo neutro possono essere caratterizzati secondo questo schema in quanto:
- esiste un insieme P* formato da elementi primi (fermioni) chiamati quark;
- tali elementi, unendosi sotto l’azione della forza nucleare forte, originano l’insieme W dei nucleoni (protoni e neutroni);
- esiste un insieme I non generabile a partire da P*. Tale insieme è formato da un leptone (elettrone) e dal bosone mediatore della forza nucleare forte (gluone).


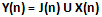





Un intetessante studio matematico che proseguira’ con altri due articoli.