Sul blog di Elettronica Open Source puoi leggere non solo tutti gli articoli Premium riservati agli abbonati Platinum 2.0 e inseriti nella rivista Firmware 2.0 (insieme ad articoli tecnici, progetti, approfondimenti sulle tecnologie emergenti, news, tutorial a puntate, e molto altro) ma anche gli articoli della Rubrica Firmware Reload. In questa Rubrica del blog abbiamo raccolto gli articoli tecnici della vecchia rivista cartacea Firmware, che contengono argomenti e temi evergreen per Professionisti, Makers, Hobbisti e Appassionati di elettronica. Il Cyclic Redundancy Code o, abbreviato, CRC, è un codice ciclico o polinomiale utilizzato per determinare la qualità di una trasmissione o per verificare il codice eseguibile presente in memoria, magari al momento del boot. Utilizzare un algoritmo CRC performante può essere utile soprattutto se abbiamo esigenze di tipo prestazionali tipiche di un sistema embedded.
Nei moderni sistemi di comunicazione lo scambio delle informazioni, in maniera comprensibile ed efficace, tra due o più entità è di fondamentale importanza. In base alla natura del segnale, le trasmissioni possono suddividersi in due gruppi principali: trasmissione di tipo analogico o di tipo digitale. Nel primo caso si utilizza un segnale continuo nel tempo. Il problema fondamentale di questa particolare trasmissione è quello dell’integrità dei dati o affidabilità, cioè occorre poter ricostruire, in ricezione, la forma d’onda del segnale trasmesso senza che questo subisca alterazioni per mezzo, magari, di disturbi. In altre parole, la trasmissione deve essere caratterizzata da un buon rapporto segnale/rumore. Al secondo gruppo appartengono le trasmissioni digitali dove si impiega un segnale numerico. Come in precedenza, anche in questo caso occorre considerare un aspetto importante quale l’integrità dei dati: nessuna perdita di bit durante la trasmissione e mantenere il sincronismo tra trasmettitore e ricevitore al fine di garantire una corretta decodifica dei dati ed eliminare i ritardi. Le trasmissioni digitali, data la natura del segnale, sono in genere meno influenzabili dai disturbi rispetto a quelle analogiche. In questo caso, la gestione degli errori può essere svolta adottando codifiche ridondanti (codici autorilevatori e autocorrettori). La comunicazione tra sistemi analogici e numerici può avvenire previa conversione dei segnali da analogico a digitale e viceversa. Un altro utilizzo dell’algoritmo di CRC è nel test della memoria RAM o per verificare l’integrità del codice presente su memoria flash a ogni successivo riavvio dell’applicazione residente su scheda: a questo proposito si veda il Listato 2.
# include <STDIO.H>
unsigned int Crc16 (char *Mess,unsigned char NumByte);
void main (void)
{
unsigned int Crc;
char Message [ ] = {0x02, 0x07};
Crc = Crc16 ( Message, sizeof (Message) );
printf (“Crc16 = % 04X\n”,Crc);
}
unsigned int Crc16 (char *Mess,unsigned char NumByte)
{
unsigned int Crc16;
char NumOfBit;
char Flag;
Crc16 = 0xFFFF;
while (NumByte > 0)
{
Crc16 = Crc16 ^ ((usigned int)*Mess) & 0x00FF;
NumOfBit = 0;
while (NumOfBit < = 7)
{
Flag = Crc16 & 0x0001;
Crc16 = Crc16 >> 1;
if (Flag ! = 0) Crc16 = Crc16 ^ 0xA001;
NumOfBit ++;
}
Mess++;
NumByte — —;
}
/* Swap Crc16*/
Crc16 = (Crc16 >> 8) | (Crc16 << 8);
return (Crc16);
}
| Listato 1: Calcolo CRC |
// Update the CRC for transmitted and received data using // the CCITT 16bit algorithm (X^16 + X^12 + X^5 + 1). unsigned char ser_data; static unsigned int crc; crc = (unsigned char)(crc >> 8) | (crc << 8); crc ^= ser_data; crc ^= (unsigned char)(crc & 0xff) >> 4; crc ^= (crc << 8) << 4; crc ^= ((crc & 0xff) << 4) << 1;
| Listato 2: Possibile algoritmo CRC-16 per applicazioni embedded |
UN PO’ DI TEORIA
Ricordiamo che nello studio dei codici si parte sempre dal concetto di alfabeto: da un determinato alfabeto composto di simboli, b, è possibile sempre istituire una codifica binaria per l’alfabeto se le rappresentazioni binarie hanno una lunghezza (espressa in numero di bit) tale che si soddisfi la relazione:
m = INTmax(log2b)
Non solo, nel mondo degli algoritmi di verifica sono presenti differenti sistemi che possono garantire la bontà dei dati nelle diverse fasi, ossia dai codici a rivelazione d’errore con autoverifica a conteggio fisso - quali il codice biquinario e il codice due su cinque - e alcuni codici con autoverifica a parità, i quali si ottengono aggiungendo un bit di controllo (nel caso più semplice bit di parità o parity-check) a un dato codice. La gestione dell’errore (rivelazione e/o correzione) nelle trasmissioni dati porta alla definizione di codifiche in cui accanto ai bit di codifica per i dati effettivi si introducono bit aggiuntivi (checkbit) assolventi a funzioni di controllo del codice, ovvero bit ridondanti (nel senso che non intervengono nella codifica dei dati). Se fissassimo con n la lunghezza della parola di un codice binario, allora si avrebbe un codice ridondante quando n > m. In questo ambito gli r = n – m bit, ridondanti, si dicono bit di controllo del codice e sono utilizzati appunto per assolvere a funzioni di controllo della codifica. Non solo, il codice è ridondante quando Dm > 1, ovvero, con D si identifica la distanza di Hamming di un codice binario con il numero di bit di cui differiscono due parole del codice. La tecnica della ridondanza consiste nell’adozione di codici nei quali ai bit dati (bit di codifica effettiva dei dati) si aggiungono bit di controllo (bit ridondanti) determinati (in numero e valore) sulla base di appositi procedimenti, la struttura del messaggio, le caratteristiche della trasmissione e, in particolare, la probabilità di errore. I codici ridondanti si suddividono in codici autorilevatori, che consentono di rilevare errori, e in codici autocorrettori, che consentono di rilevare/correggere errori. I codici autocorrettori si dicono anche codici protetti e per essi sarà importante determinare l'efficienza o grado di protezione, cioè la capacità di rilevare/correggere errori. Le capacità di rilevazione e di correzione degli errori dipendono chiaramente dalla ridondanza della codifica: più bit di ridondanza si hanno, più tali capacità aumentano (ma anche le problematiche sopra accennate). A questo proposito occorre notare che se un codice ha distanza minima di Hamming Dm allora per Dm errori si raggiunge una configurazione valida e l’errore non è più rilevabile. Il Riquadro 1 mostra alcuni codici ciclici più utilizzati secondo la loro forma polinomiale.

Riquadro 1: Polinomi generatori CRC ricorrenti
A questo riguardo possiamo pensare che il CRC-12 è più adatto per messaggi composti di caratteri di 6 bit, gli altri per messaggi composti di caratteri di 8 bit. I CRC-CCITT sono standardizzati CCITT. Non solo, per le applicazioni speciali richiedenti alta precisione si usano polinomi generatori a 32 bit (CRC-32) come ad esempio nelle trasmissioni di dati su reti TCP/IP. Nei codici CRC, spesso anche chiamati codici ciclici o polinomiali, il controllo consiste nel considerare un messaggio M da trasmettere come un polinomio M(x) e un opportuno polinomio generatore G(x): le operazioni di controllo devono ricavare da M(x) un polinomio T(x) che sia divisibile per G(x) e trasmettere il frame T corrispondente a T(x). In ricezione sarà così possibile testare l’errore dividendo il frame ricevuto per lo stesso polinomio generatore G(x). Qualora il resto di tale divisione non sia nullo, allora si sarà in presenza di errore. Proviamo a definire un codice CRC. Come prima cosa occorre identificare un messaggio, m, composto da una serie di bit, n. In questo caso disponiamo di un polinomio M(x) di grado n – 1 i cui coefficienti sono i bit del messaggio stesso, ovvero M.
Se M = 1101011011, allora il polinomio è:
M(x) = x9+x8+x6+x4+x3+x+1
A questo punto occorre considerare un polinomio generatore G(x) di grado g con grado inferiore a M(x) e g < n, oltre a disporre del termine di grado 0. Così, posto: G(x) = x4 + x + 1 allora a G(x) resta associata la stringa binaria (di 5 bit): G = 10011. A questo punto è necessario mettere paletti sulla trasmissione delle informazioni. In effetti, in trasmissione è necessario aggiungere al messaggio M composto da n bit un messaggio di controllo Mc costituito da c bit, dove è necessario che c £ g. Fatto questo, otteniamo un nuovo messaggio M’ da cui poter determinare un polinomio T(x) che sia divisibile per G(x). Il polinomio T(x) è definito rispettando alcuni requisiti, ovvero:
- costruire M’ = M + Mc ove Mc è composto di g bit “0” da accodare a M, il polinomio M’(x), corrispondente a M’, avrà grado n + g;
- fare la divisione binaria (cioè mod2) di M’(x) con G(x), per cui si avrà: M’(x) / G(x) = Q(x) + R(x);
- determinare T(x) = M’(x) – R(x); il polinomio T(x) è, per costruzione, divisibile mod2 per G(x).
In sostanza, il principio di CRC consiste nel trattare le sequenze binarie come polinomi binari, cioè polinomi i cui coefficienti corrispondono alla sequenza binaria. In questo modo la sequenza binaria 0110101001 può essere rappresentata con la forma polinomiale seguente:
0 * X9 + 1 * X8 + 1 * X7 + 0 * X6 + 1 * X5 + 0
* X4 + 1 * X3 + 0 * X2 + 0 * X1 + 1 * X0, cioè
X8 + X7 + X5 + X3 + X0 o anche
X8 + X7 + X5 + X3 + 1
In questo modo, il bit di peso minore della sequenza (il bit più a destra) rappresenta il grado 0 del polinomio (X0 = 1); il quarto bit partendo da destra rappresenta il grado 3 del polinomio (X3) e così via. Una sequenza di n bit costituisce quindi un polinomio di grado massimo n – 1.
CRC CON MSP430
Dal sito della rivista possiamo prelevare una possibile applicazione CRC per un target MSP430 scritto in due versioni: metodo bitwise o tabellare. Per prima cosa è necessario scegliere il polinomio e, in caso di metodo tabellare, occorre costruire, o generare, la tavola associata a esso. Abbiamo già scritto che la lunghezza del polinomio varia a seconda del tipo di CRC che si vuole generare e può variare da 8 a 64 fattori (es. CRC16: x16 + x15 + x13 + x12 + x4 + x3 + x2 + 1). Una volta scelto il polinomio e il tipo di CRC bisogna trasformare lo stesso nel suo valore esadecimale e non considerare il fattore con esponente uguale alla lunghezza del CRC e trasformare i restanti fattori in Hex. (es x15 + x13 + x12 + x4 + x3 + x2 + 1 = 0xB01D). Una volta effettuata questa operazione, si è pronti a generare le tavola dei valori utilizzabile per il calcolo del CRC. Per far ciò, bisogna inserire il valore del polinomio (Hex) nella define TB_POLY del file “crctable.c”, sempre scaricabile dal sito della rivista. Non solo, è anche necessario definire TB_FILE “nome del file di output”, TB_WIDTH “lunghezza in numero di byte del CRC” e TB_REVER (False/True), ovvero inversione del risultato di uscita del CRC. Solo successivamente non resta che eseguire la funzione main in crctable.c e la tavola dei valori verrà generata. In realtà, prelevando i file associati dall’application report, SLAA221–November 2004, del processore MSP430 di TI troviamo la tabella già pronta all’uso o, per la precisione, una serie di tabelle in base a ogni polinomio. Ottenuta la tavola dobbiamo inserirla nel codice sorgente che sarà poi residente in memoria attraverso una struttura dati prevista dal linguaggio utilizzato o, se avessimo la necessità, creare il corrispettivo algoritmo in VHDL: in questo caso bisogna convertire la tavola dei valori in modo da poterla integrare in una memoria interna della FPGA. L’algoritmo utilizzato è abbastanza semplice: infatti, considerando un polinomio generatore del codice di controllo con X15 + X13 + 1, cioè A001H, la Figura 1 mostra l’algoritmo utilizzato, mentre il Listato 1 pone in evidenza l’equivalente algoritmo scritto in C.
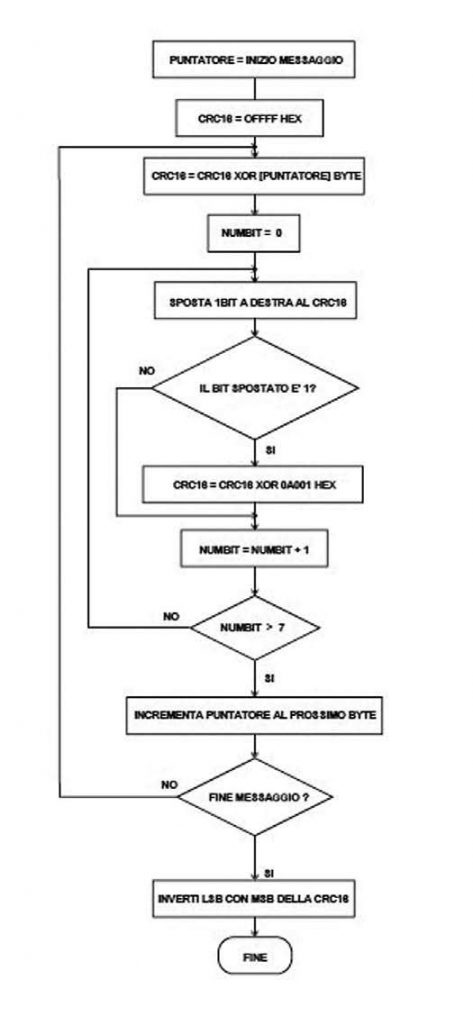
Figura 1: Algoritmo CRC
Al contrario, le Figure 2 e 3 mettono in evidenza le possibili prestazioni in ambito MSP430 utilizzando i file prelevati dalla rivista.
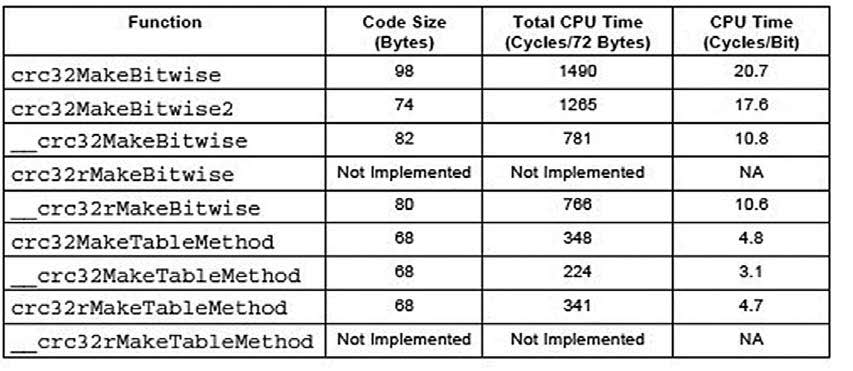
Figura 2: Tempi per CRC-32
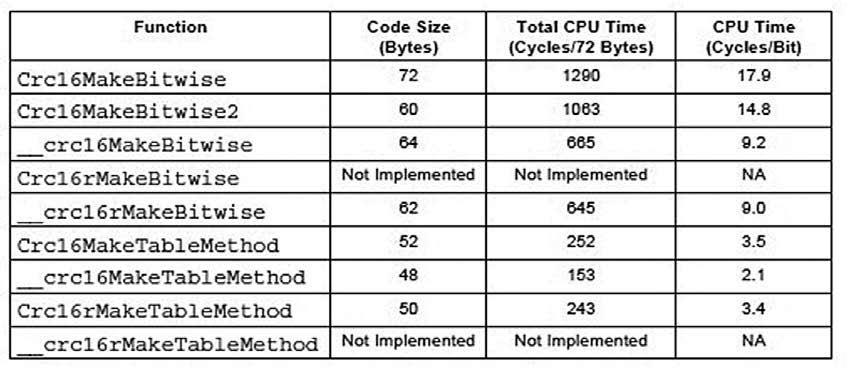
Figura 3: Tempi per CRC-16