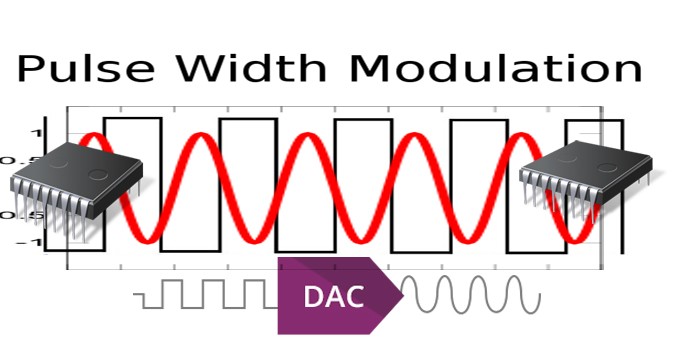
PWM è l’acronimo dei termini inglesi Pulse Width Modulation, modulazione della larghezza dell’impulso. Si tratta di una tecnica che consente di variare la potenza applicata ad un carico, mantenendo costante l’ampiezza della tensione erogata sull’utilizzatore e “variando” la durata degli impulsi applicati al carico stesso. Il carico viene quindi sottoposto ad un treno di impulsi, opportunamente calibrato e calcolato. È indubbiamente un metodo piuttosto complicato, ma permette di ridurre al minimo la dissipazione di eventuali transistor di potenza utilizzati, in quanto vengono utilizzati come semplici interruttori e non da regolatori di corrente. Definendo opportunamente la larghezza degli impulsi è possibile ottenere tensioni continue, o più in generale, forme d’onda anche molto complesse. Il PWM può essere prodotto utilizzando i microcontrollori oppure dei circuiti integrati dedicati esclusivamente a questo scopo. In questo articolo verrà illustrato come utilizzare la tecnica PWM per realizzare un convertitore digitale/analogico (DAC).
CONVERSIONE PWM/DAC
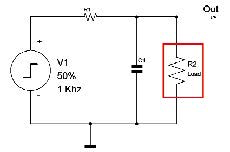
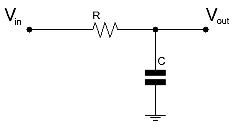
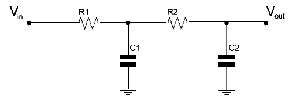
Per ottenere una tensione analogica, il treno di impulsi generato dalla tecnica PWM deve essere applicato ad un filtro passa basso che provvederà ad estrarne la componente continua (il valore medio) eliminando le componenti ad alta frequenza introdotte dal PWM. Il risultato ottenuto è quindi fortemente dipendente dal tipo di filtro adottato. Utilizzando un filtro con una frequenza di taglio troppo bassa, verrebbe compromessa la larghezza di banda del DAC, viceversa utilizzando un filtro con frequenza di taglio troppo alta sarebbe la risoluzione ad esserne condizionata. In figura 1 è riportato lo schema di principio di un PWM/DAC.
Il generatore V1 è un generatore di impulsi digitali rettangolari e nella realtà questa funzione è svolta dal microcontrollore. Nell’esempio esso fornisce una tensione pulsante digitale con livello alto pari a 5 volt e livello basso di 0 volt (rispetto a massa). La sua frequenza è fissata a 1 KHz con un duty cycle del 50% (figura 2).
Il filtro bassa basso è costituito dalla rete composta dal resistore R1 e dal condensatore C1. Il resistore R2 costituisce il carico vero e proprio e, nel dimensionamento del filtro, si dovrà fare in modo che il carico sia almeno 50 volte superiore al valore di R1 per non abbassare drasticamente la tensione d’uscita. Le due resistenze costituiscono infatti un partitore resistivo la cui la tensione massima (al nodo centrale) è data da:
UN ESEMPIO PRATICO
Si consideri lo schema elettrico di figura 1 per ottenere una tensione continua positiva di 3,3 Volt a partire da una tensione di 5V nell’ipotesi che il carico assorba una corrente di 4 mA. Ecco come procedere per la determinazione dei parametri.
Determinazione della percentuale del Duty Cycle
È ovvio che il treno di impulsi dovrà avere un duty cycle maggiore del 50%, dovendo produrre una differenza di potenziale maggiore della metà della tensione di ingresso. Per stabilire con precisione quale deve essere la percentuale di lavoro attiva (e di conseguenza quella passiva) occorre considerare la seguente formula:
dove naturalmente:
- VEFF indica la tensione da riprodurre;
- VOP (PWM) indica la tensione di picco del segnale PWM.
I due parametri percentuale indicano la porzione del periodo in cui il segnale deve trovarsi rispettivamente a livello logico alto e basso, in una successione continua di stati differenti. Naturalmente, la formula inversa consente di ricavare il valore della tensione efficace, conoscendo la percentuale del duty cycle:
Determinazione della frequenza del PWM
Ai fini della tensione generata, la frequenza non è particolarmente influente. Essa inizia ad essere rilevante quando è necessario produrre forme d’onda particolarmente complesse (e di elevata frequenza), come si vedrà in seguito. In ogni caso è sempre conveniente scegliere la massima frequenza possibile, per sfruttare tutti i vantaggi del PWM ed ottenere maggiori risoluzioni. Nell’esempio si è scelto arbitrariamente una frequenza di 1 KHz ed è importante notare che cambiando la percentuale del duty cycle, il valore della frequenza resta inalterato.
Determinazione dei componenti del filtro passa basso
Dal momento che il carico deve essere alimentato con una tensione di 3,3 Volt ed assorbire una corrente di 4mA, il relativo valore resistivo è dato da:
La conoscenza di questo valore permette di dimensionare opportunamente il filtro passa basso, evitando di “caricarlo” eccessivamente e di ridurre esageratamente la tensione d’uscita. L’utilizzo di un buon filtro influenza la bontà della tensione generata e riduce la presenza di ondulazioni ad alta frequenza, intollerabili in talune applicazioni di precisione. Tratteremo a sommi capi, in questa sede, solamente dei filtri passivi (composti solamente da resistenze, condensatori ed induttori). Utilizzando filtri attivi (realizzati con operazionali) si evita l’effetto di “caricamento” della sorgente PWM grazie alla loro elevata impedenza di ingresso. L’adozione dei filtri passivi è tuttavia più economica e semplice nelle applicazioni PWM/DAC.
Filtro passa-basso di 1° Ordine
La funzione di trasferimento per un filtro di questo tipo è data dall’equazione:
dove la costante di tempo τ è espressa in secondi. È interessante anche notare come la larghezza di banda sia data dalla formula:
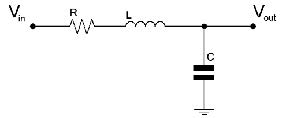
La figura 3 mostra un classico filtro bassa basso passivo di primo ordine, nel quale la costante di tempo è rappresentata dal prodotto RC. Questi tipi di filtri offrono semplicità e basso costo, ma non forniscono buone prestazioni nelle applicazioni PWM/DAC. È garantita in ogni caso la classica funzione di integratore per il segnale applicato all’ingresso.
Filtro passa-basso di 2° Ordine
Il filtro passa basso di 2° Ordine offre 40dB/decade di “stop-band rolloff” ottenendo un raddoppio delle prestazioni rispetto al precedente filtro. La funzione di trasferimento è data dall’equazione:
La larghezza di banda è data dalla formula:
Praticamente un filtro passivo di 2° Ordine è costituito dal collegamento in cascata di due filtri di 1° Ordine (in serie). È possibile utilizzare il tipo RC composto solamente da resistori e capacità, ovvero il tipo RLC, composto anche da induttori, che contribuiscono a migliorare le prestazioni del filtro stesso. Tradizionalmente gli induttori vengono evitati nelle strumentazioni e nei circuiti di controllo a causa delle loro dimensioni fisiche e della relativa deviazione di valore dal corrispondente modello matematico. Comunque, per applicazioni di tipo PWM/DAC non è tanto importante creare un filtro dall’esatta larghezza di banda.
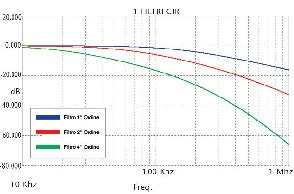
Filtro passa-basso di Ordini superiori
I filtri di ordine più elevato offrono migliori valori di “stop-band rolloff rates” e riescono a rimuovere una quantità maggiore di ripple indesiderato. Comunque la complessità del circuito e la deriva termica crescono di pari passo all’ordine del filtro stesso (Figura 4, 5 e 6). Aumentano anche i costi e lo spazio occupato sul circuito. In questi casi conviene certamente utilizzare un chip dedicato all’elaborazione del segnale PWM (DSC).
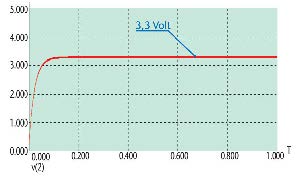
Il segnale ottenuto
Come si nota dalla figura 7, il segnale desiderato di 3,3 Volt è disponibile all’uscita della rete, con una minima presenza di ripple, ininfluente ai fini pratici. Aumentando il valore del condensatore si ottiene una tensione più pulita con una ondulazione più bassa, viceversa il ripple risulta intollerabile ma la tensione desiderata viene raggiunta in un arco di tempo minore. Se aumenta la frequenza del PWM, si può abbassare il valore del condensatore.
Codice MCU
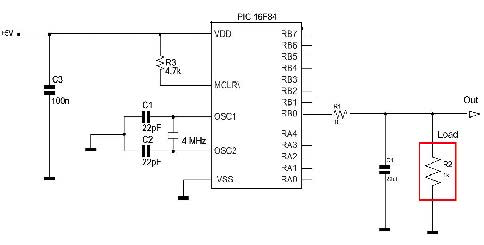
Volendo implementare la procedura all’interno di un microcontrollore si consideri lo schema della figura 8. Il generatore d’onda rettangolare adesso è rappresentato da un Pic 16F84, capace di produrre impulsi di 0V e 5V (rispettivamente valore logico basso ed alto) mentre il software è compilato con il Mikrobasic, ma l’utilizzo di qualsiasi altro pacchetto di sviluppo va senz’altro bene, sostituendo i relativi statements. Come si vede nel listato 1, la porta RB0, adibita ad uscita, è sottoposta a continui cambi di stato per produrre, tramite la tecnica del PWM, l’effetto desiderato.
rem Tensione di 3,3 Volt
program pwm01
trisb.0=0
while true
portb.0=1
delay_us(660)
portb.0=0
delay_us(340)
wend
end.
| Listato 1 |
Sono naturalmente i componenti esterni a determinare la tensione efficace voluta. Sebbene la somma temporale delle pause di attesa sia di 1000ms (pari ad 1 ms), la reale durata di un periodo (prodotta dal software del listato 1) è di 994ms. Ciò è dovuto alle istruzioni di controllo del ciclo infinito che, inevitabilmente, utilizzano qualche ciclo macchina aggiuntivo. Aumentando il clock con un quarzo e una MCU più veloci (e programmando in Assembler), tale problema viene eliminato. Posizionando un tester al punto contrassegnato con Out (uscita), si leggerà un valore di tensione continua pari a 3,3 Volt, benché il microcontrollore non sia in grado di produrre tensioni analogiche intermedie (Figura 8).
GENERAZIONE DI UN’ONDA TRIANGOLARE
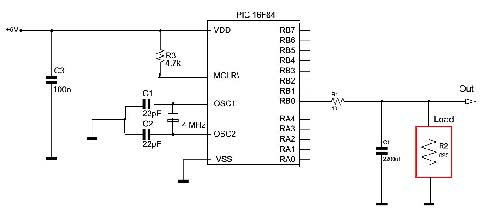
Si premette che con i microcontrollori di fascia media, la frequenza che può essere raggiunta è alquanto bassa. Questo perché il singolo campione, per poter fornire la sua piena efficienza, deve durare solo pochi nanosecondi, velocità impossibile da raggiungere per prodotti di medio livello. In ogni caso, col prossimo esempio, si vedrà come generare una forma d’onda triangolare utilizzando un microcontrollore PIC16F84. Le caratteristiche del segnale generato sono le seguenti:
- forma d’onda: triangolare;
- pendenza: lineare;
- frequenza: 50 Hz;
- periodo: 20 mS;
- ampiezza0P: 5 Volt;
- frequenza PWM: 10 Khz;
- duty Cycle: da 0% a 100%
- step: 10 ripetizioni per campione;
- ripple: <2%.
Schema elettrico
Lo schema elettrico, raffigurato in figura 9, è simile al precedente. Cambia solamente il valore del carico, ora dimensionato ad 1 Kohm e del condensatore di filtro, pari a 22 mF. Può essere tranquillamente utilizzato un quarzo da 4 MHz, anche se uno da 20 MHz garantisce una più “pronta” risposta alle istruzioni del linguaggio utilizzato. Se al pin d’uscita del microcontrollore non viene collegato alcun filtro, non si osserverà un’onda triangolare bensì un susseguirsi di onde rettangolari dal duty cycle variabile.
Processo del segnale triangolare
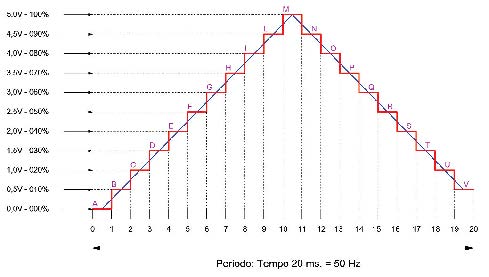
La pendenza del segnale triangolare può essere considerata come una fitta successione di tensioni crescenti e decrescenti nel dominio temporale. La relativa linearità semplifica notevolmente i calcoli. Maggiore è il numero di campioni esaminati per periodo, maggiore sarà la qualità del segnale generato. Ogni “gradino” è la risultante della generazione PWM, alle varie percentuali di duty cycle. Per poter essere più incisivo, il treno d’impulsi deve essere ripetuto più volte nel tempo, anche se l’effetto prodotto è quello di un’onda a “scalini” (figura 10). In ogni caso il filtro in uscita “pulisce” ottimamente il segnale in uscita.
Il listato Basic
Anche se abbastanza lungo, il sorgente (listato 2) contiene le procedure per generare, tramite il PWM, i valori intermedi di rampa, formando i fronti di salita e discesa dell’onda triangolare. Anche se i campioni sono “solamente” venti, la forma del segnale in uscita è rispettata, grazie anche alla relativa linearità della funzione. In ogni caso, è sempre meglio prevedere numerosi campioni. È possibile “parametrizzare” il programma, utilizzando variabili, cicli iterativi e controlli, al fine di ridurre drasticamente la lunghezza del sorgente. Implementando però tale soluzione, attraverso un linguaggio ad alto livello, si va incontro ad un “drastico” rallentamento dell’esecuzione, dovuto alle istruzioni stesse, per cui anche una pausa di alcuni microsecondi non viene interpretata correttamente come tale. Ogni modulazione a gradino è ripetuta per dieci volte, grazie alla variabile k. È possibile tuttavia ridurre il numero di iterazioni per aumentare proporzionalmente la frequenza. Si noti, sull’onda triangolare riprodotta (figura 10), la presenza di una irrilevante percentuale di ripple, che non influenza comunque la bontà del segnale ottenuto.
Il listato 2 è stato volutamente sviluppato analiticamente per motivi didattici.
rem Onda triangolare a 50 Hz
program pwm02
dim k as byte
trisb.0=0
portb.0=0
while true
rem Scalino A 0%
for k=1 to 10
portb.0=1
delay_us(0)
portb.0=0
delay_us(100)
next k
rem Scalino B 10%
for k=1 to 10
portb.0=1
delay_us(10)
portb.0=0
delay_us(90)
next k
rem Scalino C 20%
for k=1 to 10
portb.0=1
delay_us(20)
portb.0=0
delay_us(80)
next k
rem Scalino D 30%
for k=1 to 10
portb.0=1
delay_us(30)
portb.0=0
delay_us(70)
next k
rem Scalino E 40%
for k=1 to 10
portb.0=1
delay_us(40)
portb.0=0
delay_us(60)
next k
rem Scalino F 50%
for k=1 to 10
portb.0=1
delay_us(50)
portb.0=0
delay_us(50)
next k
rem Scalino G 60%
for k=1 to 10
portb.0=1
delay_us(60)
portb.0=0
delay_us(40)
next k
rem Scalino H 70%
for k=1 to 10
portb.0=1
delay_us(70)
portb.0=0
delay_us(30)
next k
rem Scalino I 80%
for k=1 to 10
portb.0=1
delay_us(80)
portb.0=0
delay_us(20)
next k
rem Scalino L 90%
for k=1 to 10
portb.0=1
delay_us(90)
portb.0=0
delay_us(10)
next k
rem Scalino M 100%
for k=1 to 10
portb.0=1
delay_us(100)
portb.0=0
delay_us(0)
next k
rem Scalino N 90%
for k=1 to 10
portb.0=1
delay_us(90)
portb.0=0
delay_us(10)
next k
rem Scalino O 80%
for k=1 to 10
portb.0=1
delay_us(80)
portb.0=0
delay_us(20)
next k
rem Scalino P 70%
for k=1 to 10
portb.0=1
delay_us(70)
portb.0=0
delay_us(30)
next k
rem Scalino Q 60%
for k=1 to 10
portb.0=1
delay_us(60)
portb.0=0
delay_us(40)
next k
rem Scalino R 50%
for k=1 to 10
portb.0=1
delay_us(50)
portb.0=0
delay_us(50)
next k
rem Scalino S 40%
for k=1 to 10
portb.0=1
delay_us(40)
portb.0=0
delay_us(60)
next k
rem Scalino T 30%
for k=1 to 10
portb.0=1
delay_us(30)
portb.0=0
delay_us(70)
next k
rem Scalino U 20%
for k=1 to 10
portb.0=1
delay_us(20)
portb.0=0
delay_us(80)
next k
rem Scalino V 10%
for k=1 to 10
portb.0=1
delay_us(10)
portb.0=0
delay_us(90)
next k
wend
end.
| Listato 2 |
Utilizzando lo stesso principio, è possibile generare anche qualsiasi altra forma d’onda periodica. La forma d’onda può essere considerata come una successione di tensioni crescenti e decrescenti nel tempo e maggiore è il numero di campioni considerati nel periodo, maggiore sarà la precisione dell’onda ottenuta. Eventualmente i valori dei campioni possono anche essere memorizzati in una memoria non volatile in modo da poter riprodurre l’onda nello stesso identico modo ad ogni riaccensione. Ovviamente in questo caso la precisione dell’onda generata va a discapito della quantità di memoria necessaria per lo storage de singoli campioni. Nel caso in cui si decide di utilizzare un filtro attivo realizzato con operazionali si deve porre attenzione allo slew rate dell’amplificatore che deve essere sufficientemente elevato in modo da supportare la massima variazione della tensione di uscita. Lo slew rate è infatti la massima pendenza della tensione di uscita dell’operazionale, è determinato dalle capacità interne dell’amplificatore e si misura in V/s. Per avere alti valori dello slew rate è possibile utilizzare amplificatori non compensati anche se la loro applicazione richiede un minimo di attenzione per evitare l’instabilità del sistema.
Conclusioni
Utilizzando microcontrollori molto veloci e l’Assembler/Assembly come linguaggio di programmazione, si possono ottenere risultati degni di nota. I dispositivi di fascia medio-bassa non garantiscono una elevata velocità ed un’ottimizzazione di codice, necessarie nelle applicazioni PWM/DAC. Utilizzando i metodi proposti nell’articolo tuttavia può essere praticamente riprodotta qualsiasi forma d’onda, ricordando sempre che il numero di punti operativi (i campioni della forma d’onda) deve risultare il più alto possibile (Figura 11).



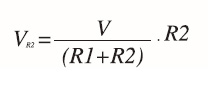
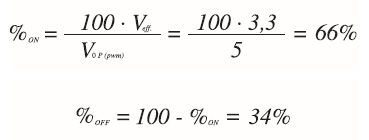
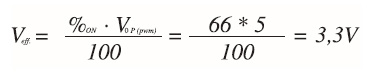

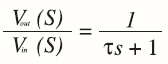
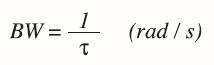
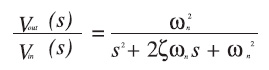
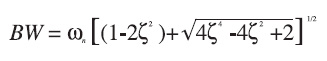




Bellissimo articolo.
Queste sono le magie dell’elettronica. In maniera magica e misteriosa vengono prodotti segnali molto diversi da quelli sorgenti. Una tecnica molto semplice, infatti, che produce un segnale “semplice” da uno più “complesso”.
Con il PWM si possono produrre qualsiasi forme d’onda, voce, canzoni, segnali vocali, ecc ecc….. E’ proprio una tecnica straordinaria!!!
Ottimo articolo, con tutti i passaggi per calcolare il filtro, grazie.
nel titolo modificherei
….la tecnica PWM per realizzare un convertitore analogico/digitale (DAC).
in
digitale/analogico
OK. Grazie.
La tecnica PWM viene utilizzata in molti ambiti, dalla variazione della velocità di un motore alle applicazioni audio passando per la gestione dei sistemi di controllo. La tecnica viene impiegata anche per gestire la luminosità del LED tra cui la dissolvenza in chiusura.