
Il microprocessore opera su una rappresentazione dei dati in forma binaria, questa non è propriamente comprensibile agli esseri umani che sono abituati ad utilizzare rappresentazioni decimali. In una notazione BCD (Binary Coded Decimal) un numero è rappresentato su quattro bits (un Nibble): il valore decimale è compreso tra 0 e 9. In questo modo, su due byte possono essere rappresentati due digits con un valore da 00 a 99. In quest’articolo, dopo un’introduzione al codice BCD, saranno illustrate alcune tecniche che ci permetteranno, al termine, di avere a disposizione una vera e propria libreria in assembler.
IL CODICE BCD
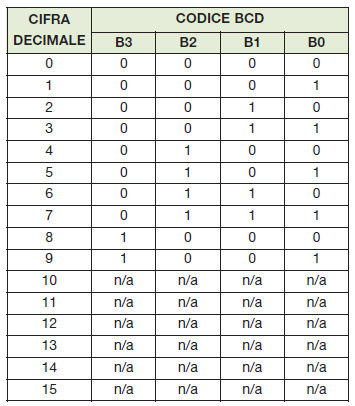
Un codice è un metodo che permette di rappresentare un insieme di simboli con un altro insieme di simboli. Se vogliamo rappresentare una cifra decimale sono necessari 4 bit (un Nibble), viene soddisfatta la relazione 23<10<24. Delle combinazioni prodotte sono utilizzate solo 10, le restanti 6 non sono considerate valide (vedi tabella 1).
Il codice BCD è un esempio di codice pesato, nel senso che ad ogni cifra decimale corrisponde una sua corrispondente binaria con il suo relativo peso. Dalla tabella 1 notiamo i vari pesi attribuiti:
b3 ha peso 8
b2 ha peso 4
b1 ha peso 2
b0 ha peso 1
Il codice BCD è anche chiamato 8421 dai coefficienti del codice stesso. Ogni cifra decimale è ottenuta dalla relazione:
Numero = 8b3 + 4b2 + 2b1 + 1b0
Può capitare di eseguire operazioni elementari di numeri espressi secondo la notazione BCD. In questo caso occorre avere l’accortezza, nelle addizioni, di aggiungere il valore decimale 6 ogni volta che il risultato dell’operazione rientra tra i valori non ammessi (le sei combinazioni che superano il valore di 9). Se per esempio, eseguiamo 41 + 5 in BCD si ottiene 46 che è un risultato ammesso; se, invece, facciamo 8 + 3 in BCD non fa 11 (non ammesso), così:
| 1 | 0 | 0 | 0 | + |
| 0 | 0 | 1 | 1 | = |
| 1 | 0 | 1 | 1 |
Ma aggiungendo 6:
| 1 | 0 | 1 | 1 | + | |
| 0 | 1 | 1 | 0 | = | |
| 1 | 0 | 0 | 0 | 1 |
otteniamo: 0001 0001 due digits su un byte. Viceversa, usando la sottrazione dobbiamo togliere 6 per le cifre che non sono lecite nel codice stesso. Per concludere questa introduzione parlerò di packed (impacchettare); se, infatti, abbiamo la necessità di rappresentare numeri decimali superiori a 10 risparmiando così spazio di memoria, allora dirò che devo impacchettare i diversi Nibble. Se devo rappresentare il numero 132, si ottiene: 132 = 0001 0011 0010.
ROUTINE ASSEMBLER
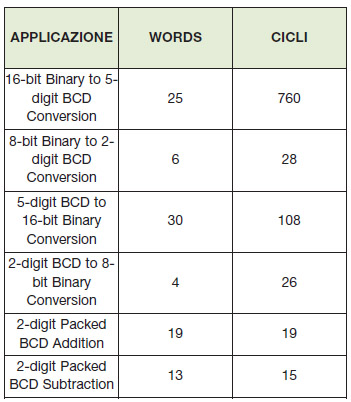
Dopo aver trattato un po’ di teoria, teniamo fede a quanto abbiamo promesso: costruire una libreria assembler per gestire correttamente conversioni numeriche utilizzando la codifica BCD. Utilizziamo il linguaggio assembler (o assembly) per meglio sfruttare la velocità e la compattezza del microprocessore. Nella tabella 2 vediamo lo spazio di memoria occupato e la velocità, in termine di cicli macchina di ciascuna routine. Dalla tabella 2 vediamo che implementeremo diverse routine ognuna con una loro peculiarità.
Esiste la possibilità di utilizzare le stesse routine su un AT90Sxx0x sostituendo alcune istruzioni presenti nel listato, in ogni caso viene indicato nel file stesso la posizione dove sostituire l’opcode con l’istruzione assembly equivalente.
16-bit Binary to 5-digit BCD Conversion
Questa routine si occuperà di convertire un valore binario rappresentato su 16-bit in un packed BCD di 5 digit. Questa implementazione sfrutterà la caratteristica chiamata Z-pointer con auto-decremento.
8-bit Binary to 2-digit BCD Conversion
Questa routine convertità un valore binario su 8 bit in un valore BCD su due digit. Il valore binario nn deve eccedere il numero 99, in questo modo il valore BCD può essere tra 0 e 99. Il valore prodotto non è impacchettato (non è packed), cioè i due digits sono rappresentati su due bytes
5-digit BCD to 16-bit Binary Conversion
Lo scopo di questa routine è quello di convertire un valore BCD packed su 5 digit verso una rappresentazione binaria su 16-bit.
2-digit BCD to 8-bit Binary Conversion
Converte un numero BCD su 2-digit in una rappresentazione binaria su 8-bit. Il valore BCD d’ingresso non è packed, nel senso che i due digit sono rappresentati su due byte.
2-digit Packed BCD Addition
Lo scopo di questa routine è quella di addizionare un valore packed BCD su 2-digit. In uscita abbiamo la somma dei due numeri in ingresso sempre come 2-digit.
2-digit Packed BCD Subtraction
Questa subroutines deve sottrarre due-digit packed secondo la rappresentazione BCD. In uscita otteniamo la differenza dei due numeri d’ingresso sempre come 2-digit packed BCD con l’eventuale riporto.
DESCRIZIONE DEGLI ALGORITMI UTILIZZATI
Passiamo ora brevemente a descrivere gli algoritmi e le scelte progettuali utilizzate. Come si legge dai listati viene utilizzato una istruzione che è una prerogativa della famiglia AVR per facilitare le operazioni in BCD. L’istruzione in questione è la “BRHC” e “BRHS”. Infatti, viene testato il bit 5 dello Status Register. Questo bit (H: Half Carry Set) indica un “Half Carry” in alcune operazioni aritmetiche ed è utilissimo nelle operazioni BCD.
bin2BCD16
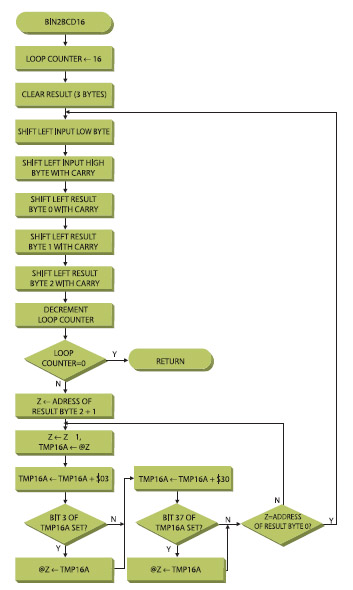
Converte un valore rappresentato su 16-bit in forma binaria in BCD. I registri utilizzati in ingresso sono identificati come “fbinH:fbinL” (Figura 1).
Parametri in ingresso
I registri utilizzati per questa operazione sono:
r16 identificato come “fbinL” – Binary Value Low Byte
r17 identificato come “fbinH” – Binary Value High Byte
Parametri di uscita
Il risultato è un valore in rappresentazione BCD su 5 digit su tre bytes: “tBCD2:tBCD1:tBCD0”. I registri utilizzati sono:
r13 “fBCD0” – BCD Digits 1 and 0
r14 “fBCD1” – BCD Digits 2 and 3
r15 “fBCD2” – BCD Digit 4
Registri interni
Registri coinvolti: r18, r19, r30 e r31
r18 identifica “cnt16a” – Contatore
r19 identifica “tmp16a” – registro temporaneo
r30 identifica ZL
r31 identifica ZH
Modalità di chiamata
Per utilizzare la subroutine nel vostro programma occorre:
- caricare i registri a 16-bit “fbinH:fbinL” con un valore da convertire(la parte alta del byte in “fbinH”);
- chiamare dal programma la subroutine “bin2BCD16”;
- il risultato è nei registri “fBCD2:fBCD1:fBCD0”: la parte MSD nel Nibble basso del byte in “fBCD2”.
Esempio
La subroutine può essere chiamata in questo modo:
;***** Conversione di 54,321 in
BCD packed format
ldi fbinL,low(54321)
ldi fbinH,high(54321)
rcall bin2BCD16 ;result:
tBCD2:tBCD1:tBCD0 = $054321
o anche
in fbinL,tcnt1l
in fbinH,tcnt1h
rcall bin2BCD16
;Convert to 2.5-byte packed BCD
format
Nota:
Questa subroutine può essere utilizzata con il modello AT90Sxx0x sostituendo l’istruzione
ld tmp16a,-Z
con
dec ZL
ld tmp16a,Z
bin2BCD8
Questa subroutine converte un valore rappresentato in 8-bit “fbin” in un valore BCD su 2-digit “tBCDH:tBCDL”. Il valore d’ingresso utilizza il registro r16. Di questa conversione vengono presentate due varianti con o senza packed BCD. Il registro utilizzato in ingresso è identificato come “fbin”, mentre quelli in uscita come “fbinH:fbinL”.
Parametri in ingresso
Il registro utilizzato per questa operazione è:
r16 “fbin” – Binary Value Byte
Parametri di uscita
Il risultato è un valore in rappresentazione BCD su 2 digit su 2 bytes: “tBCDH:tBCDL”. I registri utilizzati sono:
r16 “tBCDH” LSD of Result
r17 “tBCDL” MSD of Result
Registri interni
Nessuno.
Modalità di chiamata
Per utilizzare la subroutine nel vostro programma occorre:
- caricare il registro a 16-bit “fbin” con il valore a 16-bit da convertire;
- chiamare dal programma la subroutine “bin2BCD8”;
- infine, otteniamo il risultato MSD e LSD rispettivamente nei registri “fBCDH” e “fBCDL”
Esempio
La subroutine può essere chiamata in questo modo:
;***** Convert 55 to 2-byte BCD ldi fbin,55 rcall bin2BCD8 ;result: tBCDH:tBCDL = 0505
Nota:
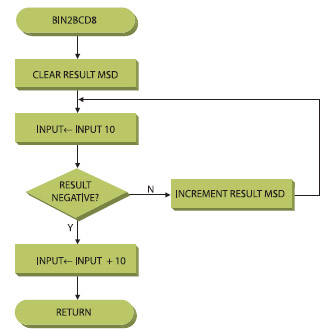
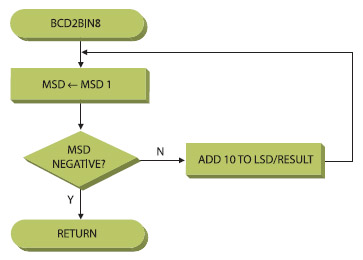
La figura 2 mostra l’algoritmo mediante i diagrammi di flusso.
L’ingresso e l’uscita condividono uno stesso registro (r16), ciò significa che qualsiasi intervento su “fbin” comporta anche ripercussioni su “tBCDL”. L’algoritmo è abbastanza semplice, infatti al valore d’ingresso viene più volte sottratto il valore 10 e, nel contempo, viene incrementato il registro “tBCDH” di una unità. Il processo termina quando viene settato il flag di Carry, in questo caso, sicuramente, si ha un valore negativo; infatti, all’ultimo giro in r16 c’è un valore tra 9<n>0, di conseguenza n-10 è sicuramente negativo: si è ottenuto la parte “tBCDL”. A questo punto si provvede a ristabilire il corretto valore aggiungendo di nuovo 10. La variante packed, non comporta sostanziali modifiche ma solo l’accorgimento che occorre lavorare sullo stesso registro. Viene eseguita la sottrazione del valore d’ingresso e, ad ogni giro positivo, viene incrementato il Nibble alto del byte del registro r17 aggiungendo il valore x10. Quando viene sollevata il flag di carry, a r17 viene semplicemente aggiunta la parte rimanente del valore di r16 utilizzando un’ addizione.
BCD2bin16
Questa subroutine converte un valore rappresentato su 5-digit packed BCD come 3 bytes (“fBCD2:fBCD1:fBCD0”) in un numero binario su 16-bit (“tbinH:tbinL”). Vengono utilizzati 7 registri: r12, r13, r14, r15, r16, r17, r18.
Parametri in ingresso
I registri utilizzati per questa operazione sono:
r16 identificato come “fBCD0” – BCD Digits and 0
r17 identificato come “fBCD1” – BCD Digits 2 and 3
r18 identificato come “fBCD2” – BCD Digit 4
Parametri di uscita
I registri utilizzati per questa operazione sono:
r14 identificato come “tbinL” – Low Byte of 16-bit Result
r15 identificato come “tbinH” – High Byte of 16-bit Result
Registri interni
I registri utilizzati per questa operazione sono:
r12 identificato come “copyL” – Temporary Value Used by “mul10a/mul10b”
r13 identificato come “copyH” – Temporary Value Used by “mul10a/mul10B”
r14 identificato come “mp10L” – Low Byte of Input to be Multiplied by “mul10a/mul10b”
r15 identificato come “mp10H” – High Byte of Input to be Multiplied by “mul10a/mul10b”
Modalità di chiamata
Per utilizzare la subroutine nel vostro programma occorre:
- caricare i tre valori “fBCD2:fBCD1:fBCD0” con i valori da convertire (MSD nella parte bassa di “fBCD2”);
- chiamare dal programma la subroutine “BCD2bin16”;
- infine, otteniamo il risultato nei registri “fbinH:fbinL”.
Esempio
La subroutine può essere chiamata in questo modo:
;***** Convert $065535 to a 16-bit binary number ldi fBCD2,$06 ldi fBCD1,$55 ldi fBCD0,$35 rcall BCD2bin16 ;result: tbinH:tbinL = $ffff (65,535)
Nota
Se poniamo “abcde” i 5-digit (a=MSD, e=LSD), la conversione è svolta secondo la seguente formula:
10(10(10(10a+b)+c)+d)+e
La subroutine “mul10a”/”mul10b” svolge l’operazione di moltiplicazione e addizione ripetuta per quattro volte durante la computazione. Questa subroutine prende la variabile a 16-bit “mp10H:mp10L” e la variabile “adder” come parametro d’ingresso. La subroutine può essere chiamata sia da “mul10a” che da “mul10b”. Infatti,
- “mul10a” – moltiplica “mp10H:mp10L” e aggiunge la parte alta del nibble di “adder”.
- “mul10b” – moltiplica “mp10H:mp10L” e aggiunge la parte bassa del Nibble “adder”.
BCD2bin8
Questa subroutine converte un valore rappresentato come 2-digit BCD (“fBCDH:fBCDL”) in un valore binario di 8-bit (“tbin”).
Parametri in ingresso
I registri utilizzati per questa operazione sono:
r16 identificato come “fBCDL” – LSD of BCD Input
r17 identificato come “fBCDH” – MSD of BCD Input
Parametri di uscita
Il registro utilizzato per questa operazione è:
r16 identificato come “tbin” – 8-bit of Result
Registri interni
Nessuno
Modalità di chiamata
Per utilizzare la subroutine nel vostro programma occorre:
- caricare i registri “fBCDH” e “fBCDL” rispettivamente con i valori MSD e LSD;
- chiamare dal programma la subroutine “BCD2bin8”;
- infine, otteniamo il risultato con rappresentazione a 8-bit in “tbin”.
Esempio
La subroutine può essere chiamata in questo modo:
;***** Convert $0403 (43) to an 8- bit binary number ldi fBCDL,3 ldi fBCDH,4 rcall BCD2bin8 ;result: tbin = $2b (43)
Nota
Di questa conversione vengono presentate due varianti con o senza packed BCD in ingresso. Se è utilizzata la variante con packed BCD allora la variabile “fBCDH” dovrà essere caricata con il valore BCD da convertire prima di chiamare la subroutine. La figura 3 dettaglia graficamente l’algoritmo di conversione.
Per l’algoritmo non packed la conversione è abbastanza breve. Infatti, la parte alta del digit BCD (registro r17) viene sottratta di una unità, mentre al valore di uscita (r16), che corrisponde anche a “fBCDL”, viene incrementato di 10. Il valore di “fBCDH” è utilizzato come contatore alla conversione. In questo modo: “fBCDH” * (10 + “fBCDL”). Per la versione packed occorre tenere presente che il numero si trova in un byte, su due Nibble, quindi la sottrazione non è fatta con 1 (della parte alta del NIbble), ma con x10.
BCDadd
Questa subroutine esegue l’addizione di due valori in formato 2-digit BCD unsigned, identificati come “BCD1” and “BCD2”. Il risultato è restituito in “BCD1” con il suo overflow in “BCD2”.
Parametri in ingresso
due valori binari da addizionare e convertire nel formato BCD mediante l’uso dei registri r16 e r17.
r16 identificato con mnemonico “BCD1” BCD
Number 1
r17 identificato con mnemonico “BCD2” BCD
Number 2
Parametri di uscita
Il risultato viene restituito nel registro r16 con il riporto in r17:
r16 “BCD1” – BCD Result
r17 “BCD2” – Overflow Carry
Registri interni
R18 identificato con mnemonico “TMPADD”
Modalità di chiamata
Per utilizzare la subroutine nel vostro programma occorre:
- carica i valori “BCD1” e “BCD2” con i valori da sommare;
- chiama dal programma la subroutine “BCDadd”;
- infine, otteniamo il risultato in “BCD1” con il suo relativo overflow in “BCD2”
Esempio
La subroutine può essere chiamata in questo modo:
;***** Add BCD numbers 51 and 79
ldi r16,$33
ldi r17,$4F
rcall BCDadd
;result: BCD2:BCD1=$0130
Nota
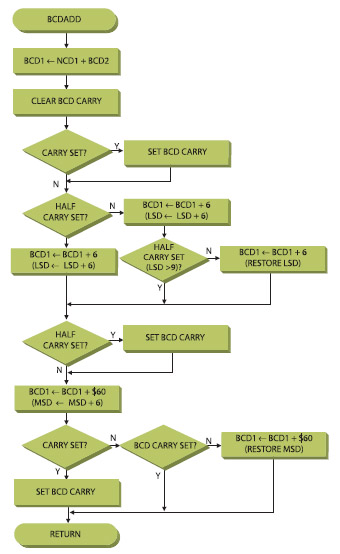
Il risultato dell’addizione tra due BCD sono passati in BCD1 e l’eventuale overflow è riportato nel registro BCD2. Dopo aver caricato la costante 6 al registro di lavoro interno, si procede a sommare i valori binari ed in seguito viene trattata la conversione in BCD. Si applica l’aggiustamento del valore decimale sommando 6 ogni volta che il risultato della conversione non rientra nella codifica BCD. La figura 4 descrive graficamente l’algoritmo.
In questa subroutine si utilizza la prerogativa della famiglia AVR, vale a dire la possibilità dell’Half Carry Flag.
BCD2sub
Questa subroutine si occupa di sottrarre due numeri in formato BCD (2-digit packed BCD).
Parametri in ingresso
I due valori BCD da sottrarre mediante l’uso dei registri r16 e r17.
r16 “BCDa” – BCD Number to Subtract From
r17 “BCDb” – BCD Number to Subtract
Parametri di uscita
Il risultato viene restituito nel registro r16 con il riporto in r17
r16 “BCD1” – BCD Result
r17 “BCD2” – Underflow Carry
Registri interni
Nessuno
Modalità di chiamata
Per utilizzare la subroutine nel vostro programma occorre:
- carica il valore “BCDa” e “BCDb” con i valori da sottrarre;
- chiama dal programma la subroutine “BCDsub”;
- infine, otteniamo il risultato in “BCDa” con il suo relativo underflow in “BCDb”.
Esempio
La subroutine può essere chiamata in questo modo:
;***** BCD numbers 72 - 28
ldi BCDa,$72
ldi BCDb,$28
rcall BCDsub
;result: BCDb=$00 (positive
result), BCDa=44
Oppure, in caso di risultato negativo:
;***** Subtract BCD numbers 0 - 90
ldi BCDa,$00
ldi BCDb,$90
rcall BCDsub
;result: BCDb=$01 (negative
result), BCDa=10
Nota
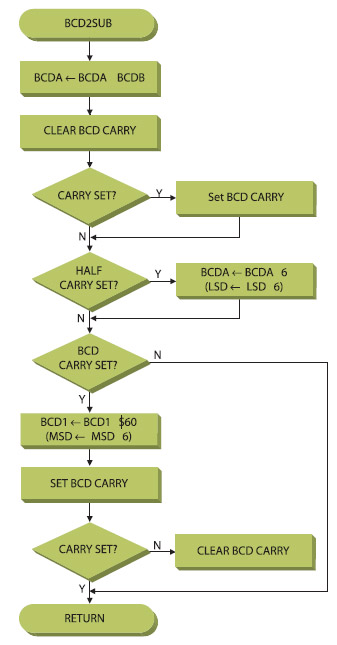
Il risultato della sottrazione tra due BCD è posto in BCDa e l’eventuale riporto è nel registro BCDb. Dopo aver fatto l’operazione di sottrazione binaria, si procede a fare la conversione nel formato BCD. L’algoritmo è illustrato in figura 5.
Anche in questa conversione si tiene conto del risultato dell’operazione controllando se rientra nella codifica BCD.
CONCLUSIONE
A questo punto abbiamo a disposizione una libreria in assembler/assembly (al seguente link un link di approfondimento) per la gestione del formato BCD. Sono un insieme di subroutines che non presentano difficoltà per adattarle alla propria cross-factory, inoltre dispongono di un alto grado d’efficienza per essere utilizzate in un’applicazione reale. È possibile scaricare dal sito della rivista tutti i listati relativi alle routines descritte.





Lavorare con i bit non è semplice, disporre di una libreria può senz’altro essere di aiuto nella gestione di vari algoritmi.